| Issue |
Int. J. Simul. Multidisci. Des. Optim.
Volume 14, 2023
|
|
|---|---|---|
| Article Number | 19 | |
| Number of page(s) | 20 | |
| DOI | https://doi.org/10.1051/smdo/2023021 | |
| Published online | 14 December 2023 | |
Research Article
Parameter optimization of titanium-coated stainless steel inserts for turning operation
Department of Mechanical Engineering, Vel Tech Rangarajan Dr. Sagunthala R&D Institute of Science and Technology, Avadi, Chennai − 600062, Tamil Nadu, India
* e-mail: karthick@veltech.edu.in
Received:
10
April
2023
Accepted:
12
November
2023
This study discusses the three essential process parameters cutting speed, feed and depth of cut on the quality of the tool during turning operation. A high-strength stainless steel tool coated with tungsten carbide is used. The tool is further strengthened using cryogenic treatment by immersing it in liquid nitrogen for 24 h and 36 h respectively. The surface roughness of the simple coated tool and the processed tool is compared using optimization techniques like the Taguchi technique and ANOVA. The analysis revealed that the surface roughness of the simple coated tool insert was 0.5 μm, whereas the surface roughness of the tool inserts immersed in liquid nitrogen for 36 h was 12.5 μm. The processed tool insert became brittle which lead to an increase in surface roughness after the turning operation. Three different algorithms like Grass Hopper Optimization, Moth Flame Optimization, and Salp Swarm Optimization were used to observe the feasibility of the optimization techniques. The Moth Flame Optimization algorithm had good convergence and also delivered results that were correlating with the ANOVA. It is concluded that while keeping a high tool rotation speed of 984.46 rpm, a low feed of 91.4 mm/min and a depth of cut of 0.25 mm resulted in a low surface roughness of simple coated tool insert was 0.59 μm.
Key words: Coated tool insert / turning / optimization techniques / surface roughness
© K. Muniyappan and L. Nagarajan, Published by EDP Sciences, 2023
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The turning operation is a metal-cutting process that is used to remove excess materials and also produces desired shapes in a given part. The turning operations can be semiautomatic as in the case of lathe machines or can be fully automated with the help of computerized turning machines. A single-point cutting tool is used to carry out the turning operation. Typically, the cutting tool is held stationary in a vice or tool holder while the material is made to rotate along a fixed axis. The pointed tool removes a small layer of the rotating material while performing the turning operation. The quality of the turning operation and smoothness of the finished workpiece depends on factors like rotation, depth of cut, and cutting force. The turning operation is a traditional metal cutting operation that has been performed ever since the industrial revolution and the invention of the lathe. According to Yadav et al. [1], machining parameters like spindle speed, feed, and depth of cut influence the change in hardness caused on the material surface due to turning operations. In the experiments, EN 8 metal was used as the workpiece, and coated carbide tools were used as the tools. The hardness after turning was measured on the Rockwell scale. Several turning parameters were optimized by Shivade et al. [2] for turning on EN8 steel using a single response optimization method. Taguchi's L9 Orthogonal array design is used in experiments. In this paper, an investigation into the use of the Taguchi parameter is discussed. In their work [2], they optimized Surface Roughness and Tool tip temperature in turning operations using single-point carbide cutting tools.
During turning operations on various steel grades, Deshpande et al. [3] reviewed various parameters like surface roughness, MRR, and tool wear. Cutting speed, feed rate, depth of cut, and tool wear were some of the turning input parameters in various papers, while surface roughness, cutting forces, tool wear and MRR were some of the output parameters. The Taguchi and RSM approaches have been used in several research studies to design and optimize parameters. Using tungsten-coated carbide tools to turn Aluminum Alloy 7075, Alagarsamy et al. [4] describe Taguchi design of experiments methodology. A standard orthogonal array design based on L27 provides three process parameters for material removal rate and machining time, which are cutting speed, feed, and depth of cut. Using the physical vapour deposition technique, Lakshmanan et al. [5] fabricated WC inserts with a single-layered AlCrN-based coating. A carbide insert was examined for micro-hardness, coating thickness, surface morphology, and elemental composition. Using conventional and cryogenic coolants (LN2), turning operations were performed on Ti-6Al-4V alloys with coated carbide (AlCrN-cc) and without coated carbide inserts. In an experiment, we measured the roughness value and turning forces for different feeds, depths of cuts, and cutting speeds.
According to Ezugwu et al. [6], titanium machining has many problems such as tool wear and failure mechanisms. Straight tungsten carbide (WC/Co) cutting tools continue to remain superior in nearly all titanium alloy machining processes, even though Chemical Vapour Deposition (CVD) coated carbides and ceramics haven't been able to replace cemented carbides as they react with titanium and were relatively low in fracture toughness and thermal conductivity. Xiaoping et al. [7] discuss potential research issues regarding machining titanium and its alloys. Because of their exceptional corrosion resistance and high strength-to-weight ratio, titanium and its alloys are highly attractive materials. Aerospace has been titanium's major application. Researchers Kainz et al. [8] have developed a multi-layered coating architecture that consists of two alternating hard materials that enhance the mechanical properties of hard coatings in the metal cutting industry. CVD TiN/TiBN multilayer coatings were correlated with their microstructures in this work, and they were compared to their single-layer counterparts. A thermal CVD plant prepared multilayers with different bilayer periods (1400, 800, 300, and 200 nm) by varying the composition of the feed gas alternately.
According to Alborz et al. [9], cryogenic milling has been the focus of their research. End milling Ti–6Al–4V titanium alloy with cryogenic cooling and conventional dry and flood cooling is compared. Various combinations of cutting parameters were tested in machining experiments. Micro-hardness was measured for each sample under subsurface conditions and surface roughness was examined. In a milling experiment with various nose radiuses, Emel [10] found that adhesion, abrasion, chipping, and fracture are the main mechanisms and modes of tool failure. Regardless of cutting speed and milling direction, cutting forces decreased with an increase in nose radius, excluding up-milling at cutting speed over 90 m/min. It was observed that roughness decreased with increasing nose radius and speed in the experiments. Up milling resulted in lower surface roughness and forces than down milling. The study revealed that the increase in nose radius caused an increase in edge serration in chip morphology.
Fernandez-Valdivielso et al. [11] proposed a new testing method to detect the important dimensional parameters and grades of carbide inserts for turning of nickel alloys regarding surface reliability. Gandarias et al. [12] discussed the controversy surrounding the cryogenic treatment of steels. Though cryogenic treatment is effective in some cases, such as in HSS steels, its effectiveness in carbide inserts is still debated. Pereira et al [13] discussed the cryogenic treatment of AP23 steel using carbon dioxide. They inferred that the tool life increased by 12% and the surface roughness decreased after subjecting the tool to cryogenic treatment. Polvorosa et al. [14] in their study presented, the results recorded during turning operations to find flank and notch wear were summarized, using cooling at above 5 bars. They inferred that large-grain alloy indicates high-notch wear. However, smaller grain size results in high flank wear. Amigo et al. [15] predicted the cutting force and tool wear during high-speed turning of Nimonic superalloy. With cutting speeds lower than 100 m/min, the wear prediction model produced relative errors of less than 5%, and with speeds higher than 100 m/min, it produced errors of less than 14%. By increasing tool life x3 (from 8 to 24 min), reducing the side cutting edge angle also contributed to the improvement in tool life. A study conducted by Zhang et al. [16] discussed the use of in-process stochastic tool wear identification as a method for improving micro milling force modelling. To predict stochastic tool wear values, they proposed improving the integrated estimation technique based on the long short-term memory (LSTM) network and particle filter algorithm. By considering the influence of tool wear, they found that micro-cutting tool availability and sustainability have improved, and prediction accuracy has increased by 3.4% as well.
Sivalingam et al. [17] carried out the optimization of process parameters for various machining environments using an evolutionary algorithm. Three different case studies were considered during their study. A comparison was made between the MFO algorithm and genetic algorithms, grasshopper algorithms, grey wolves, and particle swarm optimization algorithms in order to evaluate the effectiveness of the MFO algorithm. The results showed that the MFO algorithm outperformed the other algorithms in terms of performance.
Dhilip et al. [18] discussed on turning of hardened non-shrinking die steel having Rockwell hardness of 45 to 70. They attempted to maximize the material removal rate with minimal machining time and surface roughness. Optimization was carried out using the L9 algorithm. Grey relational analysis was used for optimizing the output characteristics.
Rana [19] optimized the machining performance of CNC tool inserts coated with tungsten carbide coating under dry cutting. The coating was carried out using the CVD method. The average evaluated Vickers Hardness was found to be 1455HV and 951HV for both coated as well as uncoated samples respectively. This shows a 53% rise in the hardness of the uncoated tungsten carbide inserts.
Das et al. [20] used machine learning to optimize the turning capability of AISI D6 steel. There are various ML approaches that can be used to model different response variables, including polynomial regression, random forest regression, gradient boosted trees, and adaptive boosting regression based on adaptive boosting. The complexity of the models was suited to optimize the turning characteristics with high accuracy. However, the calculations demanded high-end computing systems to finish the calculation within a reasonable time.
Sobh et al. [21] used the Taguchi technique to optimize the turning parameters of the titanium alloy tool insert. Three levels of cutting parameters were used in the experiment, each with three different levels, so that three different cutting parameters could be varied. A variety of cutting speeds were experimented with, such as 80, 100, and 120 m/min, variable feed rates were used, such as 0.05, 0.1, and 0.15 mm/rev, and variable cutting depths were varied as 0.2, 0.4, and 0.6 mm, respectively. There were two significant parameters that appear to be important in determining the level of surface roughness and wear of the tool inserts: the cutting speed and the cutting depth.
The surface roughness of AISI steel inserts coated with CVD coatings was optimized based on the turn parameters and the insert geometry of Vukelic et al. [22]. In order to achieve the best results, the machined parts were machined at various speeds, feed rates, depths of cut, corner radiuses, rakes, as well as angles of approach and inclination. In order to derive an empirical, regression model for arithmetical mean surface roughness, the roughness of the surface was measured after each experiment, and statistical analysis was used to generate the model. The results of the study demonstrate that the developed model can be applied in a practical manner.
In a review of tool life optimization and their effectiveness on tool inserts, Kamble et al. [23] presented a review of tool life optimization. For the purpose of predicting the life of tools, a variety of methods and approaches have been considered here, such as Taguchi methods and regression analyses. They concluded that the Taguchi technique using the observations in regression analysis can effectively calculate the feed rate and depth of cut constants and also the tool life.
Using cryogenically treated tools in hardened hot work tool steel turning, Nas and Zbek [24] conducted an investigation into optimizing the machining parameters through the use of cryogenically treated tool materials. They optimized their performance using Taguchi L18, a method that was developed based on gray relational analysis with Taguchi L18. Dry turning tests were performed using carbide cutting tools that had been cryogenically treated as well as those that had not been treated. According to the results of the analysis, the feed rate (72.84%) was identified as the dominant factor that affected surface roughness and the cutting speed (93.93%) was identified as the dominant factor that affected flank wear.
During the side milling of DAC 55 steel, Tomadi et al. [25] performed an optimization analysis on the size of the cut and the radius of the cutting edge during the side milling process. During the machining operation, they aimed to optimize both the radius of the cutting edge of the tools as well as the width of the cut when the tools were used. The width of the cut appears to have the greatest influence on the quality of the surface roughness when compared to the radius of the cutting edge when it comes to improving the quality of the surface roughness.
Akgun and Kara [26] through optimization techniques analysed the cutting tool coating effect on surface roughness and cutting force during the turning of AA6061. TiB2 was coated on the tool insert using PVD technique. The mathematical models for the cutting force and surface roughness were developed through linear and quadratic regression models. The results indicated that the best performance in terms of Fc and Ra was obtained at an uncoated insert, cutting speed of 350 m/min, feed rate of 0.1 mm/rev, and depth of cut of 1mm. Moreover, the feed rate is the most influential parameter on Ra and Fc, with 64.28% and 54.9%, respectively.
Arunkarthikeyan and Balamurugan [27] used multi objective optimization technique to find the performance improvement of cryo treated inserts on turning of AISI 1018 steel. Dry turning operation was conducted according using Taguchi's L9 orthogonal array using 3 factors and 3 levels to find the tool wear rate and surface roughness. They suggested that MRGRA gives better results on cryo treated WC-Co inserts when machining of AISI 1018 steel.
Several pieces of literature pointed out the influence of the turning tool parameters on the finishing quality of the turned workpieces. Studies made on tool inserts revealed that operating parameters like tool geometry, material being machined, and effectiveness of coolant determine the operating life of the tool. Optimization techniques were carried out to improve the machining capability of the tool inserts without sacrificing their service life. However, there are other qualities like the strength of the tool, its tribological property and corrosion that also influences the quality of the turning operation. In this paper multi-criteria decision-making approach is adopted to optimize the parameters that deliver a good finish turning on the workpiece. The experiment is carried out using a tungsten carbide-coated stainless-steel tool insert. The coated insert is subjected to hardening under cryogenic temperature. The surface roughness of the tool insert after the turning operation is optimized. A reliable optimization technique is selected and optimized parameters are determined through this study.
2 Materials and methods
2.1 Experimental setup
For the experiment, a custom-450 grade stainless steel of diameter 89 mm and length 510 mm is used. The tool insert is coated with tungsten carbide (WC). The coating is carried out through the electroplating method till the 650 nm layer of the tungsten carbide was deposited over the stainless steel. The coating is strengthened with the help of cryogenic treatment. For this, the coated tool insert was dipped in liquid nitrogen. Three different approaches were used in this experiment. At first, the electro-coated tool insert without any post-treatment is considered. Secondly, the coated tool insert is subjected to cryogenic treatment by dipping the insert in liquid nitrogen for 12 h. Finally, the coated tool insert is subjected to cryogenic treatment by dipping the insert in liquid nitrogen for 36 h. The tool inserts thus produced and subjected to cryogenic treatment are used to carry out turning operations on mild steel workpieces. After that, the surface roughness of the tool insert is determined. The surface roughness of the coated tool inserts (Ra), 12 h cryogenically treated insert (Rq), and 36 h cryogenically treated insert (Rz) are found using optimization techniques.
2.2 Optimization using Taguchi technique
Optimization is conducted using Taguchi's L27 orthogonal array technique. In the L27 array, thirteen columns are used to tabulate the experimental parameters and their correlation. For the three-factor three-level experiment set, the total number of experiments that should be carried out is 27. These experimental combinations were carried out for all three sets of inserts. In this study, three different control factors with three different levels. The turning operation was carried out on a centre lathe with variable speed and feed drive with a tool dynamometer setup as a force measurement device. For each experiment, a fresh cutting edge is used. Each machining operation is carried out for 1 min of duration. For each experiment, the feed force (Fx), thrust force (Fy), and cutting force (Fz) are tabulated by means of a piezoelectric tool post dynamometer. The surface roughness value for each machined surface is found precisely using a probe-type surface roughness tester. The control factors were cutting speed (N), feed (F) and Depth of cut (D). Table 1 shows the values assigned to the three different parameters. The cutting speed is varied from 850 pm to 1050 rpm. The feed is varied from 60 mm/min to 180 mm/min. The depth of cut is varied from 0.25 mm to 0.75 mm. The surface roughness is measured in μm.
L27 array and values of the turning parameters.
2.3 Optimization using ANOVA technique
The surface roughness of the coated tool inserts (Ra), 12h cryogenically treated insert (Rq), and 36h cryogenically treated insert (Rz) is determined using the ANOVA technique. Equation (1) shows the regression equation used for Ra. Table 2 shows that the linear approach is used during ANOVA. It is observed that the p-Value for the model was less than 0.05. This reveals that the ANOVA model is statistically significant and is taken into consideration for the study. Table 3 shows the coefficients obtained during the analysis of Ra. From Table 4 it is found that the model has around 95% fit.
Equation (2) shows the regression equation used for Rq. Table 5 shows the F values and P Values measured during ANOVA. It is observed that the p-Value for the model was less than 0.05. This reveals that the ANOVA model is statistically significant and is taken into consideration for the study. Table 6 shows the coefficients obtained during the analysis of Rq. From Table 7 it is found that the model has around 97% fit.
Equation (3) shows the regression equation used for Rz. Table 8 shows the F values and P Values measured during ANOVA. It is observed that the p-Value for the model was less than 0.05. This reveals that the ANOVA model is statistically significant and is taken into consideration for the study. Table 9 shows the coefficients obtained during the analysis of Rz. From Table 10 it is found that the model has around 90% fit.
Three different algorithms are used in this study to arrive at an optimized value of the surface roughness of the tool inserts. The pseudo-code for Grass Hopper Optimization (GHO) algorithm is provided below.
Initialize the swarm Xi (i=1,2,3,….,n)
Initialize Cmax, Cmin and itemax
Calculate the fitness of each agent
T = the best search agent
While (I < itemax)
Compute non-dominated solutions
Compute the best solution based on the crowding distance (F1j)
Update the achieve size
Update C
For each search agent
Normalize the distance between the grasshoppers
Update the position of current search agent
Bring the current search agent back if it goes outside the boundaries
End for
Update T if there is a better solution
I = I + 1
End While
Print the best solution
The pseudo-code for Moth Flame Optimization (MFO) algorithm is provided below.
Initialize the parameters for Moth-flame
Initialize Moth position Mi randomly
For each I = 1:n do
Calculate the fitness function fi
End For
While (iteration ≤ max-iteration) do
Compute non-dominated solutions
Compute the best solution based on the crowding distance (F1j)
Update the achieve size
Update the position of Mi
Calculate the no. of flames
Evaluate the fitness function fi
If (iteration==1) then
F = sort (M)
OF = sort (OM)
Else
F = sort (Mt-1, Mt)
OF = sort (Mt-1, Mt)
End if
For each I = 1:n do
For each j=1:d do
Update the values of r and t
Calculate the value of D w.r.t. corresponding Moth
Update M(i,j) w.r.t. corresponding Moth
End For
End For
End While
Print the best solution
The pseudo-code for the Salp Swarm Optimization (SSO) algorithm is provided below.
Salp Population Initialization (Pij) i=1,2,3…ns and j=1,2,3…np
While (it<=max_it)
For each salp i=1 to ns/
Calculate fitness functions Ra, Rq and Rz
End For
Compute non-dominated salps
Compute the best salp as the food source based on the crowding distance (F1j)
Update the achieve size
Calculate the value of c1 using 
Update Leader position P1j using
If c3<0
P1j = F1j − c1[(ubj − lbj)c2 + lbj]
Else
P1j = F1j + c1[(ubj − lbj)c2 + lbj]
End
For each salp i=2 to ns
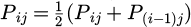
End For
Check Pij with in lbj and ubj
End While
Display the positions and its fitness values of salps from archive.
Table 11 shows the parameters used while using the GHO algorithm. Whereas Table 12 shows the parameters used in MFO and SSO algorithms respectively.
Analysis of Variance for Ra.
Coefficients for Ra.
Model Summary for Ra.
Analysis of Variance for Rq.
Coefficients for Rq.
Model Summary for Rq.
Analysis of Variance for Rz.
Coefficients for Rz.
Model Summary for Rz.
GHO algorithm parameters.
MFO and SSO algorithm parameters.
3 Result and discussion
Figure 1 shows the Pareto chart for the standard effects taken for the surface roughness of the simple coated tool insert, i.e., Ra. The term ‘A’ represents the cutting speed (N), ‘B’ represents the feed (F) and ‘C’ represents the depth of cut (D). From the figure, it is found that the feed given through the tool insert had a higher affinity to increase the surface roughness. However, the combination of the feed and depth of cut provides a negligible surface roughness. Figure 2 shows the residual plots obtained for Ra. The plots reveal that the normal plot is in close correlation with the residue. Similarly, the frequency of the residue is closer to the centre. This phenomenon reveals the goodness of fit and that the optimization carried out provides reliable results. Figure 3 shows the summary of the report obtained for Ra which also provides favourable result during the study.
Figure 4a shows the RSM plot for Ra and compared it with two process parameters of turning, i.e., F and N. It is observed that for a low value of feed (F), the surface roughness Ra remains low irrespective of changes in cutting speed (N). The Ra value varies closer to unity. However, as the feed is increased, the surface roughness increases to a great extent. The surface roughness significantly increases when the cutting speed is low while maintaining a high feed. This causes the highest roughness which reaches 2.46 μm. This phenomenon is also observed for low cutting speed while maintaining a high feed. Thus, in comparison, it is found that the feed has greater influence than the cutting speed to control the surface roughness of the coated tool insert.
Figure 4b shows the RSM plot for Ra and compared it with two process parameters of turning, i.e., N and D. It is observed that for a low value of depth of cut (D), the surface roughness Ra remains low. However, the cutting speed should be maintained between 900 mm/min and 1000 mm/min to get a low surface roughness of 0.8 μm. However, further reduction in the cutting speed results in increasing the surface roughness of the coated tool insert. A considerable increase in the surface roughness of 1.35 μm is noted for a low cutting speed of 840 rpm and high depth of cut, i.e., 0.8 mm. It is inferred that the cutting speed has a greater influence on the surface roughness than the depth of the cut.
Figure 4c shows the RSM plot for Ra and compared it with two process parameters of turning, i.e., F and D. It is observed that for a low value of feed and low depth of cut, the surface roughness Ra remains considerably low i.e., 0.5 μm. While maintaining the low cutting speed, the surface roughness is observed to increase very slightly with an increase in the depth of cut. However, the surface roughness increases exponentially to 2 μm when the feed is increased irrespective of the depth of cut.
Figure 5 shows the Pareto chart for the standard effects taken for the surface roughness of the simple coated tool insert, i.e., Ra. The term ‘A’ represents the cutting speed (N), ‘B’ represents the feed (F) and ‘C’ represents the depth of cut (D). From the figure, it is found that the feed given through the tool insert had a very high affinity to increase the surface roughness. However, the combination of the feed and depth of cut provides a negligible surface roughness. Figure 6 shows the summary of the report obtained for Ra which also provides favourable result during the study. This phenomenon reveals the goodness of fit and that the optimization carried out provides reliable results.
Figure 7a shows the RSM plot for Rq and compared it with two process parameters of turning, i.e., F and N. It is observed that for a low value of feed (F), the surface roughness Rq remains low irrespective of changes in cutting speed (N). The Ra value varies closer to unity. However, as the feed is increased, the surface roughness increases to a great extent. The surface roughness significantly increases when the cutting speed is low while maintaining a high feed. This causes the highest roughness which reaches 3 μm. This phenomenon is also observed for low cutting speed while maintaining a high feed. Thus, in comparison, it is found that the feed has greater influence than the cutting speed to control the surface roughness of the coated tool insert.
Figure 7b shows the RSM plot for Rq and compared it with two process parameters of turning, i.e., N and D. It is observed that for a low value of depth of cut (D), the surface roughness Rq remains low i.e., 0.5 μm. However, the cutting speed should be maintained at 1050 mm/min to get a low surface roughness of 0.8 μm. However, further reduction in the cutting speed results in increasing the surface roughness of the coated tool insert. A considerable increase in the surface roughness of 1.75 μm is noted for a low cutting speed of 840 rpm and high depth of cut, i.e., 0.8 mm. It is inferred that the cutting speed has a greater influence on the surface roughness than the depth of cut.
Figure 7c shows the RSM plot for Rq and compared it with two process parameters of turning, i.e., F and D. It is observed that for a low value of feed and low depth of cut, the surface roughness Rq remains considerably low i.e., 0.5 μm. While maintaining the low cutting speed, the surface roughness is observed to increase very slightly with an increase in the depth of cut. However, the surface roughness increases exponentially to 2.5 μm when the feed is increased irrespective of the depth of cut.
Figure 8 shows the Pareto chart for the standard effects taken for the surface roughness of the simple coated tool insert, i.e., Rz. The term ‘A’ represents the cutting speed (N), ‘B’ represents the feed (F) and ‘C’ represents the depth of cut (D). From the figure, it is found that the feed given through the tool insert had a very high affinity to increase the surface roughness. However, the combination of the feed and depth of cut provides a negligible surface roughness. Figure 9 shows the residual plots obtained for Rz. The plots reveal that the normal plot is in close correlation with the residue. Similarly, the frequency of the residue is closer to the centre. Figure 10 shows the summary of the report obtained for Ra which also provides favourable result during the study. This phenomenon reveals the goodness of fit and that the optimization carried out provides reliable results.
Figure 11a shows the RSM plot for Rz and compared it with two process parameters of turning, i.e., F and N. It is observed that for a moderate feed of 100 mm/min, the surface roughness Rz remains low irrespective of changes in cutting speed (N). Reduction in the feed increases the surface roughness to 5 μm. On the other hand, increasing the feed to 175 mm/min results in a tremendous increase in the surface roughness, i.e., 12.5 μm. Thus, in comparison, it is found that the feed has greater influence than the cutting speed to control the surface roughness of the coated tool insert.
Figure 11b shows the RSM plot for Rz and compared it with two process parameters of turning, i.e., N and D. It is observed that for a low value of depth of cut (D), the surface roughness Rz remains low i.e., 3.25 μm. However, the cutting speed should be maintained at 1050 mm/min to get a low surface roughness of 0.8 μm. Further reduction in the cutting speed results in increasing the surface roughness of the coated tool insert. A considerable increase in the surface roughness of 5.85 μm is noted for a low cutting speed of 840 rpm and high depth of cut, i.e., 0.8 mm. It is inferred that the cutting speed has a greater influence on the surface roughness than the depth of cut.
Figure 11c shows the RSM plot for Rz and compared it with two process parameters of turning, i.e., F and D. It is observed that for a low value of feed and low depth of cut, the surface roughness Rz remains considerably low i.e., 2 μm. While maintaining the low cutting speed, the surface roughness is observed to increase very slightly with an increase in the depth of cut. However, the surface roughness increases exponentially to 10 μm when the feed is increased irrespective of the depth of cut.
The three different optimization techniques, i.e., GHO, MFO, and SOO were used to find the influence of the process parameters i.e., cutting speed, feed and depth of cut on the surface roughness of the coated tool insert. The surface roughness (Ra) of the simple coated tool insert is compared with the post-coated inserts that were dipped in liquid nitrogen for 24h (Rq) and 36h (Rz) respectively. Table 13 shows the optimum process parameters of the three different surface roughness measured using the GHO technique. It is inferred that the post-treatment increased the brittleness of the tool insert. Because of this the strength of the tool insert increased but underwent microscopic abrasion during the turning process. As the result, the surface roughness increased proportionally with the time taken by the tool insert inside the liquid nitrogen. Tables 14 and 15 show the optimum process parameters of the three different surface roughness measured using MFO and SSO techniques respectively. Each of these techniques projected a different value of surface roughness for the given combination of the process parameters. Comparatively, the MFO technique delivered are having less deviation from the initial value of the surface roughness.
Figures 12 to14 show the summary of the three different optimization techniques used in this study. The spatial distribution obtained during the optimization is projected through the respective plots. The GHO plots show that it is skewed towards the right which shows that the values do not converge. On the other hand, the SSO plot shows that it is skewed towards the left which shows that the values do not converge. However, the MFO technique shows that its values are converging well.
Table 16 shows the process parameters that delivered lower surface roughness for the simple coated tool insert and the two post-processed tool inserts. These values were compared against the three algorithms used in this study. It is revealed that the simple coated tool insert exhibited lower surface roughness irrespective of the algorithm used. Table 17 shows the statistical performance of the three different algorithms considered for this study. From the table, it is found that the MFO technique delivered lower IGD and SP values than the other techniques. Hence, the values assigned to the process parameters of the MFO technique were incorporated into the GHO and SSO techniques. Table 18 shows the variation in surface roughness of the simple coated tool inserts under various process parameters. It is found that the surface roughness minimised considerably in the GHO and SSO techniques after incorporating the values of the MFO technique respectively.
Figure 15 shows the convergence plots of Ra, Rq, and Rz for the three different algorithms respectively. It is found that the MFO technique converged quickly irrespective of the process and post-process used on the coated tool insert.
 |
Fig. 1 Pareto chart for the standard effects for Ra. |
 |
Fig. 2 Residual plots for Ra. |
 |
Fig. 3 Summary report for Ra. |
 |
Fig. 4 RSM for Ra. |
 |
Fig. 5 Pareto chart for the standard effects for Rq. |
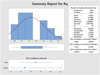 |
Fig. 6 Summary report for Rq. |
 |
Fig. 7 RSM for Rq. |
 |
Fig. 8 Pareto chart for the standard effects for Rz. |
 |
Fig. 9 Residual plots for Rz. |
 |
Fig. 10 Summary report for Rz. |
 |
Fig. 11 RSM for Rz. |
Optimum process parameters using GHO.
Optimum process parameters using MFO.
Optimum process parameters using SSO.
 |
Fig. 12 Distribution plot for GHO technique. |
 |
Fig. 13 Distribution plot for MFO technique. |
 |
Fig. 14 Distribution plot for SSO technique. |
Parameter and surface roughness for algorithm.
Statistical performance of algorithms.
Surface roughness using different algorithm.
 |
Fig. 15 Convergence plots. |
4 Conclusion
The surface roughness of the tungsten carbide-coated tool inserts subjected to turning operation was compared to treated inserts that were immersed in liquid nitrogen for 24 h and 36 h respectively. The ANOVA optimization technique delivered compatible results of the surface roughness with the Taguchi L27 technique. Response Surface Methodology revealed that the tool feed had a higher influence on the surface roughness than the cutting tool speed and depth of cut. It was revealed that for high cutting speed when the tool feed and depth of cut were low the surface roughness was around 0.5 μm. Tool inserts subjected to strengthening using liquid nitrogen became brittle and as the result, they exhibited high surface roughness of around 12.5 μm. Out of the three techniques, the Moth Flame Optimization showed good convergence. The Moth Flame Optimization technique exhibited values that were having good correlation with the ANOVA. It is concluded that for the turning process parameters of 984.46 rpm, 91.4 mm/min and 0.25 mm depth of cut, the surface roughness of the simple coated tool insert was 0.59 μm.
Author's contributions
Karthick Muniyappan: Literature survey, Preliminary investigation, Methodology of the research, Data interpretation, Inference of the study, Result and discussion
Lenin Nagarajan: Supervision of the study, Selection of optimization techniques, ANOVA study, Manuscript correction, Conclusion
References
- A. Yadav, A. Bangar, R. Sharma, D. Pal, Optimization of turning process parameters for their effect on En 8 material work piece hardness by using Taguchi parametric optimization method, Int. J. Mech. Ind. Eng. (IJMIE) 1, 17–33 (2015), ISSN No 2231–6477 [Google Scholar]
- S. Shivade, S. Bhagat, S. Jagdale, A. Nikam, P. Londhe, Optimization of machining parameters for turning using Taguchi approach, Int. J. Recent Technol. Eng. (IJRTE) 3:1, 145–149 (2014) ISSN: 2277–3878 [Google Scholar]
- R.R. Deshpande, R. Pant, Optimization of process parameters for CNC turning using Taguchi methods for en-8 alloy steel with coated/uncoated tool inserts, Int. Res. J. Eng. Technol. 04, 180–188 (2017) [Google Scholar]
- S.V. Alagarsamy, P. Raveendran, S. Arockia Vincent Sagayaraj, S. Tamil Vendan, Optimization of machining parameters for turning of aluminium alloys 7075 using Taguchi method, Int. Res. J. Eng. Technol. 6, 22–38 (2016) [Google Scholar]
- S. Lakshmanan, M. Pradeep Kumar, M. Dhananchezian, N. Yuvaraj, Investigation of monolayer coated WC inserts on turning Ti-alloy, 35:7, 826–835, DOI: 10.1080/10426914.2020.1711930 [Google Scholar]
- E.-O. Ezugwu, Z.-M. Wang, Titanium alloys and their machinability-a review, J. Mater. Process. Technol. 68, 262–274 (1997) [CrossRef] [Google Scholar]
- Y. Xiaoping, L.-C. Richard, Machining titanium and its alloys, Int. J. Mach. Sci. Technol. 3, (1999) [Google Scholar]
- C. Kainz, N. Schalk, M. Tkadletz, C. Mitterer, C. Christoph, Microstructure and mechanical properties of CVD TiN/TiBN multilayer coatings, Surf. Coat. Technol. 370, 311–319 (2019) [CrossRef] [Google Scholar]
- S. Alborz, D. Vimal, S.-T. Newman, Investigation of the effects of cryogenic machining on surface integrity in CNC end milling of Ti-6Al-4V titanium alloy, J. Manuf. Processes. 21, 172–179 (2016) [CrossRef] [Google Scholar]
- K. Emel, Nose radius and cutting speed effects during milling of AISI 304 material, Mater. Manuf. Processes. 32, 185–192 (2017) [CrossRef] [Google Scholar]
- A. Fernández-Valdivielso, L.N. López De Lacalle, G. Urbikain, A. Rodriguez, Detecting the key geometrical features and grades of carbide inserts for the turning of nickel-based alloys concerning surface integrity, Proc. Inst. Mech. Eng., Part C: J. Mech. Eng. Sci. 230, 3725–3742 (2016) [CrossRef] [Google Scholar]
- A. Gandarias, L.N.L. de Lacalle, X. Aizpitarte, A. Lamikiz, Study of the performance of the turning and drilling of austenitic stainless steels using two coolant techniques, Int. J. Mach. Mach. Mater. 3, 1–17 (2008) [Google Scholar]
- O. Pereira, A. Rodríguez, A. Fernández-Valdivielso, J. Barreiro, A.I. Fernández-Abia, L.N. López-De-Lacalle, Cryogenic hard turning of ASP23 steel using carbon dioxide, Proc. Eng. 132, 486–491 (2015) [Google Scholar]
- R. Polvorosa, A. Suárez, L.N.L. de Lacalle, I. Cerrillo, A. Wretland, F. Veiga, Tool wear on nickel alloys with different coolant pressures: comparison of alloy 718 and Waspaloy, J. Manuf. Process. 26, 44–56 (2017) [CrossRef] [Google Scholar]
- F.J. Amigo, G. Urbikain, L.N. López de Lacalle, O. Pereira, P. Fernández-Lucio, A. Fernández-Valdivielso, Prediction of cutting forces including tool wear in high-feed turning of Nimonic® C-263 superalloy: a geometric distortion-based model, Measurement 211, 112580 (2017) [Google Scholar]
- X. Zhang, T. Yu, P. Xu, J. Zhao, In-process stochastic tool wear identification and its application to the improved cutting force modeling of micro milling, Mech. Syst. Signal Process. 164, 108233 (2022) [CrossRef] [Google Scholar]
- V. Sivalingam, J. Sun, S.K. Mahalingam, L. Nagarajan, Y. Natarajan, S. Salunkhe, E.A. Nasr, J. PauloDavim, H.M.A.M. Hussein, Optimization of process parameters for turning Hastelloy X under different machining environments using evolutionary algorithms: a comparative study, Appl. Sci. 11, 9725 (2021) [CrossRef] [Google Scholar]
- J.D.J. Dhilip, J. Jeevan, D. Arulkirubakaran, M. Ramesh, Investigation and optimization of parameters for hard turning of OHNS steel, Mater. Manuf. Processes. 35, 1113–1119 (2020) [CrossRef] [Google Scholar]
- R. Rana, L. Krishnaia, Q. Murtaza, R.S. Walia, Optimizing the machining performance of CNC tools inserts coated with diamond like carbon coatings under the dry cutting environment, J. Eng. Res. - ICARI Special Issue, 4, 142–152 (2021). https://doi.org/10.36909/jer.ICARI.15327 [Google Scholar]
- A. Das, S.R. Das, J.P. Panda, A. Dey, K.K. Gajrani, N. Somani, N. Gupta, Machine learning based modelling and optimization in hard turning of AISI D6 steel with newly developed AlTiSiN coated carbide tool, Comp. Sci. 15, 43–54 (2022). https://doi.org/10.48550/arXiv.2202.00596 [Google Scholar]
- A.S. Sobh, E.M. Sayed, A.F. Barakat, R.N. Elshaerr, Turning parameters optimization for TC21 Ti-alloy using Taguchi technique, J. Basic Appl. Sci. 12, 1–25 (2023) [Google Scholar]
- D. Vukelic, M. Prica, V. Ivanov, G. Jovicic, I. Budak, O. Luzanin, Optimization of surface roughness based on turning parameters and insert geometry, Int. J. Simul. Model 21, 417–428 (2022) [CrossRef] [Google Scholar]
- P. Kamble, S. Kulkarni, S. Marathe, U. Kamble, S.B. Barve, H. Mech Dept, Review of tool life optimization methods and their effectiveness for turning inserts, Int. J. Res. Eng. Appl. Manag. 5, 85–88 (2019). https://doi.org/10.35291/2454-9150.2020.0114 [Google Scholar]
- E. Nas, N.A. Özbek, Optimization of the machining parameters in turning of hardened hot work tool steel using cryogenically treated tools, Surf. Rev. Lett. 27:5, 26–42 (2020). https://doi.org/10.1142/S0218625×19501774 [Google Scholar]
- S.H. Tomadi, N.F.H.A. Halim, A.N. Dahnel, A.S. Rosman, G. Umma Sankar, L.J. Eng, Optimization study on width of cut and cutting-edge radius during side milling of DAC 55 steel, Lect. Notes Mech. Eng. 33, 214–216 (2022) [CrossRef] [Google Scholar]
- M. Akgün, F. Kara, Analysis and optimization of cutting tool coating effects on surface roughness and cutting forces on turning of AA 6061 alloy, Adv. Mater. Sci Eng. 2021, 1–12 (2021) [CrossRef] [Google Scholar]
- Turning studies of AISI 1018 steel using multi objective optimization. International Conference on Computational Intelligence for Smart Power System and Sustainable Energy, CISPSSE 5, 29–32 (2020). https://doi.org/10.1109/CISPSSE49931.2020.9212247 [Google Scholar]
Cite this article as: Karthick Muniyappan, Lenin Nagarajan, Parameter optimization of titanium-coated stainless steel inserts for turning operation, Int. J. Simul. Multidisci. Des. Optim. 14, 19 (2023)
All Tables
All Figures
 |
Fig. 1 Pareto chart for the standard effects for Ra. |
| In the text | |
 |
Fig. 2 Residual plots for Ra. |
| In the text | |
 |
Fig. 3 Summary report for Ra. |
| In the text | |
 |
Fig. 4 RSM for Ra. |
| In the text | |
 |
Fig. 5 Pareto chart for the standard effects for Rq. |
| In the text | |
 |
Fig. 6 Summary report for Rq. |
| In the text | |
 |
Fig. 7 RSM for Rq. |
| In the text | |
 |
Fig. 8 Pareto chart for the standard effects for Rz. |
| In the text | |
 |
Fig. 9 Residual plots for Rz. |
| In the text | |
 |
Fig. 10 Summary report for Rz. |
| In the text | |
 |
Fig. 11 RSM for Rz. |
| In the text | |
 |
Fig. 12 Distribution plot for GHO technique. |
| In the text | |
 |
Fig. 13 Distribution plot for MFO technique. |
| In the text | |
 |
Fig. 14 Distribution plot for SSO technique. |
| In the text | |
 |
Fig. 15 Convergence plots. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.







