| 期号 |
Int. J. Simul. Multidisci. Des. Optim.
卷号 16, 2025
|
|
|---|---|---|
| 文献编号 | 8 | |
| 页数 | 8 | |
| DOI | https://doi.org/10.1051/smdo/2025007 | |
| 网上发表时间 | 2025年5月14日 | |
Research Article
Multi-head surface mounting placement optimisation based on adaptive multi-point crossover operator
School of Electrical Engineering, Yancheng Institute of Technology, Yancheng 224051, PR China
* e-mail: zhangchunfu@ycit.edu.cn
Received:
20
May
2024
Accepted:
31
March
2025
Using different sequencing of component pick-and-place on a Surface Mount Technology (SMT) machine significantly impacts the distance required for head movement. The optimisation problem of surface mounting process optimisation in multi-head gantry-type SMT machine is generally considered to be an NP-hard problem. Therefore, study divides the surface mounting process optimisation into three sub-problems and propose a two-stage optimisation algorithm. In the first stage, a balanced distribution strategy (BDS) is introduced to address the component allocation problem, and a nearest neighbour algorithm (NNA) is proposed to solve the initial feeder allocation problem and component pick-and-place sequencing problems. Due to the large scale of the problem, finding the optimal solution within a reasonable time frame is challenging. Therefore, in the second stage, a novel genetic operator is proposed to further optimise the feeder sequence and the component pick-and-place sequence. Experimental results demonstrate that the proposed algorithm achieves high precision and speed. Specifically, compared with the minimum criterion genetic algorithm, the average distance is reduced by 4.15%, and compared with the multi-swarm discrete firefly algorithm, the average distance is reduced by 7.02%.
Key words: PCB assembly / SMT machine / surface mounting process optimisation / genetic operator
© Z. Song and C. Zhang, Published by EDP Sciences, 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The SMT machine is a device used to mount electronic components onto printed circuit boards (PCBs), and its operational efficiency significantly affects PCB production. The distance travelled by the pick-and-place machine varies considerably depending on the sequence in which components are mounted. A longer travel distance will substantially increases the time required for component placement. Therefore, optimising the pick-and-place process has become a key challenge. As the most widely used type of pick-and-place machine, the gantry-type surface mount technology (SMT) machine has become a focal point of current research. The optimisation of the gantry-type SMT machine's mounting process typically involves three sub-problems: the component allocation problem (CAP), feeder assignment problem (FAP), and component sequencing problem (CSP). These problems are often modelled as Quadratic Assignment Problems (QAP) and travelling salesman problems (TSPs) (TSP), which are recognised as NP-hard problems in the field of combinatorial optimisation [1]. To address these challenges, two primary optimisation strategies have emerged. The first strategy focuses on optimising individual sub-problems while disregarding the influence of others. The second strategy aims to optimise all sub-problems simultaneously through an integrated approach. Given the high complexity of SMT machines and the mounting process, researchers have developed various methods to effectively tackle these issues.
Pi et al. [2] proposed a Finite Potential Game Heuristic Algorithm (FPGHA) to optimise the workload distribution of dual-gantry SMT machines. The algorithm generates game agents using an improved clustering method and key productivity metrics, and determines the Nash equilibrium. Experimental results demonstrate that FPGHA exhibits high effectiveness and accuracy in both simulated and real-world industrial PCB assembly scenarios, outperforming other algorithms and optimisation software. Castellani et al. [3] modified the local search process of the standard bee algorithm, by incorporating five new combinatorial optimisation operators, to optimise the FAP and CSP. Hsu and Yang [4] proposed a new swarm intelligence-based metaheuristic algorithm called Improved Shuffled Frog-Leaping Algorithm 2 (I-SFLA2), which simultaneously addresses the FAP and CSP. Mumtaz et al. [5] used a mixed-integer linear programming (MILP) model to simultaneously solve a two-level planning problem and proposed a new hybrid spider monkey optimisation (HSMO) algorithm. Hsu [6] proposed a multi-swarm discrete firefly algorithm (MDFA) to simultaneously address the CSP and FAP. Chen et al. [7] proposed an improved spider monkey optimisation (ISMO) algorithm for solving the component allocation problem (CAP) and CSP in the PCB industry.
The consideration of mutual influence among various sub-problems in the placement model and constraints has led to the increased use of heuristic algorithms. Researchers are actively investigating these algorithms to discover efficient and effective solutions that optimise the overall performance of SMT machines. By incorporating the interdependencies among component allocation, feeder assignment, component sequencing, and nozzle assignment, these heuristic algorithms provide promising approaches for improving optimisation outcomes in the optimisation process. In the work [8], a series of methods were proposed to solve each sub-problem: (i) equalising “workloads” assigned to the gantries, (ii) using a quantity ratio method, (iii) using two similarity measurement mechanisms in a modified differential evolution algorithm with a random-key encoding mapping method that to address component height restrictions, (iv) and a combination of nearest-neighbour search and 2-opt method to plan each placement operation. proposed a two-stage framework and developed a hybrid approach to solve three printed circuit board assembly (PCBA) problems: CSP, FAP, and NAP. Hsu. [9] proposed a two-stage framework and developed a hybrid approach to solve three printed circuit board assembly (PCBA) problems: CSP, FAP, and NAP. A mixed-integer programming (MIP) model is proposed by Lu et al. [10] to decompose the optimisation problem of the SMT machine into three sub-problems: feeder allocation, component assignment, and pick-and-place (PAP) sequencing. They proposed an efficient hierarchical framework with three elaborately designed heuristic algorithms to address these problems. Computational experiments, conducted using both industrial data and randomly generated data, demonstrate that the heuristic algorithm designed in this paper achieved near-optimal solutions, with an average gap of 9.93% compared to the proposed MIP model, and outperforms mainstream studies in terms of efficiency. Zhu et al. [11] proposed a novel mechanism combining the curve matching method based on discrete Fréchet distance with evolutionary algorithms to transform the pick-and-place sequence optimisation problem into a multi-objective optimisation problem for solution. Li et al. [12] proposed a hierarchical multi-objective heuristic (HMOH) that models the PCBA as the head task assignment problem (HTAP) and the pick-and-place sequencing problem (PAPSP). These two models consider all factors that affect assembly time, including pick-and-place (PAP) cycle count, nozzle changes, and simultaneous pick-and-place and PAP distance. HTAP is used to optimise NAP and CAP, while PAPSP is used to optimise FAP and CSP. Huang et al. [13] proposed a fast multi-objective hierarchical optimisation method to solve NAP, FAP, and CSP problems in a layered manner. He et al. [14] developed a multi-phase planning heuristic algorithm (mPhase) to solve NAP, FAP, CSP, and gantry cycle scheduling problems for a dual-delivery SMT placement machine. For the spin-head SMT machine, reference [15] proposed the average Chebyshev linkage directed search (ACLDS) algorithm to solve NAP, FAP, and CAP problems. Additionally, reference [16] introduced an adaptive clustering genetic algorithm to optimise the dual-gantry component placement machine for pick-and-place operations. The optimisation objectives included NAP, CAP, FAP, and CSP. In the study by Zhong et al. [17], a multi-objective scheduling optimisation method for PCB assembly lines was proposed based on an improved spider monkey algorithm. The objective was to simultaneously minimise the maximum completion time (Cmax), total energy consumption (TEC), and total maintenance time (TMT). By comparing with traditional optimisation methods including SMO, NSGA-III, DE, and PSO using production data from a company, the results showed that the ISMO algorithm was able to obtain Pareto solutions with better convergence and diversity. Liu et al. [18] proposed a two-stage hybrid MILP approach to describe the allocation of nozzle types and component heads, assigning feeders to slots, and determining component pick-up and placement sequences in multi-head SMT machines. They also introduced a two-stage problem-solving framework based on a hybrid evolutionary algorithm (HEA). The MILP formulation and HEA framework aimed to optimise the efficiency and performance of the machine by effectively addressing the allocation and sequencing challenges in the assembly process. In their study, Gao et al. [19] proposed a new Hierarchical Multi-Objective Heuristic (HMOH) framework and decomposed the pick-and-place machine assembly problem into two models. These models considered all the factors that affect the assembly time, including the number of pick-and-place (PAP) cycles, nozzle changes, simultaneous pickups, and PAP distances. Specifically, the first model, HTAP, consisted of nozzle assignment and component allocation, while the second model, PAPSP, comprised place allocation, feeder set assignment, and place sequencing problems. The HMOH framework aimed to optimise the assembly process by addressing these sub-problems in a coordinated and efficient manner. In the study by Wu et al. [20], a coding scheme and corresponding genetic operators were developed to address the scheduling optimisation problem in multi-head robotic pick-and-place machine assembly. Based on the minimum criterion principle, a minimum criterion genetic algorithm was proposed to simultaneously solve the CAP, FAP, and CSP. The algorithm aimed to optimise the assembly process by effectively addressing these sub-problems in a coordinated and efficient manner.
After conducting statistical analysis of the literature reveals that, The optimisation of the surface mounting process is a highly complex problem. Many studies have focused only on sub-problems or employed strategies to optimise certain sub-problems before applying heuristic algorithms to optimise the remaining ones. Genetic algorithms are the most widely used heuristic algorithms for surface mounting process optimisation. Several limitations arise when applying genetic algorithms to SMT machine assembly optimisation. Genetic algorithms have perform poorly for infeasible solutions, and the incorporation of constraints that accompany actual production into the genetic algorithm model often significantly increases computation time. Furthermore, genetic algorithms are not effective in utilising the working characteristics of the SMT machine assembly process, and a single genetic algorithm is fails to meet fast production requirements.
To address the aforementioned issues, this paper proposes a two-stage optimisation strategy that is based on the working characteristics of the gantry-type SMT machine assembly process. In the first stage, a Balanced Distribution Strategy is utilised to optimise the Component Allocation Problem (CAP) by taking into account the characteristics of the gantry-type SMT machine assembly process. Additionally, an initial feeder allocation and component pick-up sequence are optimised using a Nearest Neighbour Algorithm. In the second stage of optimisation, an improved genetic algorithm that is based on an adaptive crossover strategy is proposed to simultaneously solve the Feeder Assignment Problem (FAP) and Component Sequencing Problem (CSP) of the SMT machine.
2 Problem description and model establishment
Figure 1 depicts the structural model of the gantry-type SMT machine equipped with four suction nozzles. The placement head is manoeuvred by the X and Y-axis arms, allowing it to move from the initial point to the feeders. It sequentially picks up the four components required for the first cycle and places them on the designated positions of the PCB. Once the component placement for the first cycle is completed, the placement head returns to the feeders to repeat the aforementioned pick-and-place steps. This process continues until the final pick-and-place cycle is completed.
Based on the aforementioned assembly steps, the distance model for the pick-and-place process of a PCB using a gantry-type SMT machine can be formulated as follows:
 (1)
(1)
where, D denotes the total placement distance, d0 represents the distance from the initial point to the first pick-up point at the feeder by the placement head, 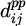 represents the distance between the i-th and j-th components placed on the PCB,
represents the distance between the i-th and j-th components placed on the PCB,  represents the distance between the i-th and j-th components picked up from the feeder,
represents the distance between the i-th and j-th components picked up from the feeder, 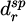 denotes the distance the placement head travels to pick up the first component in each cycle,
denotes the distance the placement head travels to pick up the first component in each cycle,  denotes the distance from the last component in each cycle back to the feeder, de denotes the distance the placement head travels from the last component to the initial (home) point, NC is the n is the total number of components, NR is the total number of placement cycles.
denotes the distance from the last component in each cycle back to the feeder, de denotes the distance the placement head travels from the last component to the initial (home) point, NC is the n is the total number of components, NR is the total number of placement cycles.
Taking into account the complexity and structural differences of the actual operation of the gantry-type SMT machine, the following constraints are proposed:
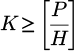 (2)
(2)
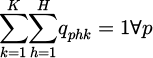 (3)
(3)
 (4)
(4)
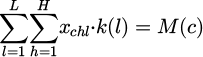 (5)
(5)
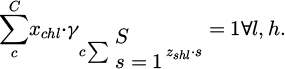 (6)
(6)
The maximum number of placement cycles is constrained by Formula (2). Formula (3) imposes restrictions on the kth placement cycle, permitting placement head h to place only one component. Formula (4) ensures that each component is assigned at least one feeder. Formula (5) limits the number of placement points for each component. Additionally, Formula (6) guarantees that within any cycle group, the placement head handling component type c picks up components exclusively from a feeder containing c-type components.
 |
Fig. 1 Architectural diagram of a gantry-type SMT machine. |
3 Initial component allocation strategy
3.1 Balanced distribution strategy
In general, an SMT machine is equipped with multiple suction nozzles, each capable of handling various component types. The suction nozzles pick up components from the feeders in a back-and-forth manner. With each placement cycle, the components picked up in the subsequent cycle differ from those in the previous one. Widely dispersed components lead to an increased total placement distance. However, maintaining consistency in the component types between adjacent pick-and-place cycles can significantly reduce travel distance.
Considering the aforementioned factors, we propose a Balanced Distribution Strategy that ensures consistency in adjacent pick-and-place cycles while achieving a balanced component load for each nozzle. This strategy aims to minimise prolonged idle movement of the nozzles. An illustrative example of the strategy is outlined below:
Step 1 involves arranging the components of each type in descending order based on their quantities. These components are then allocated to their respective nozzles for simulated placement. This allocation process is shown in Figure 2a.
Step 2 begins with the placement of the allocated component type NZ4, as shown in Figure 2b. Subsequently, the remaining components of type NZ5, which have the highest quantity, are allocated to nozzle H4. This allocation process is depicted in Figure 2c.
Step 3 involves continues the simulated component placement until all components of types NZ3 and NZ5 are placed. At this stage, no components are allocated to nozzles H3 and H4, and only component type NZ6 remains. To address this, half of the remaining NZ1 components, which possess the highest quantity, are allocated to nozzle H3. The remaining NZ6 components are then assigned to nozzle H4, as illustrated in Figures 2d-2e.
In the final step, if no unallocated component types remain and the maximum difference in component load (quantity) among the nozzles does not exceed two, further splitting is not performed, and the simulated component placement process is terminated.
 |
Fig. 2 Nozzle Component Allocation Diagram :(a) arranging the components of each type in descending order based on their quantities ; (b)-(c) NZ4 components, having the lowest quantity are mounted first, followed by assigning the most numerous NZ5 components to nozzle H4 ; (d)-(e) Simulated placement continues until all components of types NZ3, NZ5, and NZ6 are placed ; (f) If there are no remaining unassigned component types and the difference in component quantities among the nozzles does not exceed 2, the simulated mounting process is terminated. |
3.2 Feeder allocation strategy
The SMT machine's nozzles are responsible for the bidirectional transfer of components between the PCB and the feeders. The frequency of nozzle movements increases with the quantity of components of a particular type. By placing components with higher quantities closer to the PCB, the total travel distance for that type is significantly reduced. Consequently, arranging all the feeders in descending order of component quantity on both sides of the PCB's centreline can minimise nozzle travel distance between the PCB and the feeders, as illustrated in Figure 3.
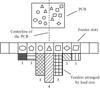 |
Fig. 3 Feeder Arrangement Diagram. |
3.3 Nearest neighbour algorithm
The proposed Balanced Distribution Strategy in Section 3.1 has been used to assign all remaining component types to each nozzle. However, in a single printed circuit board (PCB), multiple components typically exist of the same type. In the actual assembly process, determining the sequence is crucial in which each nozzle retrieves components from the feeders and places them on the PCB. To address this, we introduce a Nearest Neighbour Algorithm to determine the initial placement sequence. The algorithm comprises the following steps:
Step 1: Set the component group closest to the head as the first group to be placed. Calculate the distance the head must move to sequentially pick up components from the feeders, and update the position of the head after collecting the last component.
Step 2: Select the first component from the collected group and place it at the nearest placement point on the PCB. Calculate the distance from the remaining components on the head to their corresponding placement points on the PCB. Choose the closest placement point and place the component. Repeat this step until all components on the current head are placed.
Step 3: Calculate the distance from the last placement point to the first remaining component in the remaining placement cycles. Select the component group with the shortest distance as the next placement cycle.
Step 4: Repeat Steps 1 to 3 until all components corresponding to the placement cycles are placed. The flowchart for determining the placement sequence using the Nearest Neighbour Algorithm is shown in Figure 4.
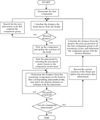 |
Fig. 4 The flowchart of the Nearest Neighbour Algorithm. |
4 Improving genetic algorithms
4.1 Adaptive multi-point crossover operator
In the initial stage of solving the feeder arrangement problem using a genetic algorithm, it is recommended to have a relatively large number of crossover points, to increase the breadth of random search and obtain a near-global optimal solution. However, in the later stages of the algorithm, crossover points should be decreased to refine solutions in the local search space.
Therefore, we propose an adaptive multi-point crossover operator:
 (7)
(7)
where F is the number of crossover points, T denotes the total number of iterations in the algorithm, t is the current iteration of the algorithm, and R rounds to the nearest integer.
As illustrated in the example depicted in Figure 5, assume the total number of iterations is 20. If the current iteration is 3 and F = 4, two parent chromosomes of the feeder are randomly selected with a 4-point crossover applied. On the other hand, if the current iteration is 16, then a 2-point crossover is performed.
 |
Fig. 5 Illustration of the adaptive crossover operator: (a) In the early stages of iteration, perform a 4-point crossover on the parent chromosomes; (b) Offspring generated from the 4-point crossover; (c) In the later stages of iteration, perform a 2-point crossover on the parent chromosomes; (d) Offspring generated from the 2-point crossover. |
4.2 Mutation operator
The mutation operator helps maintain diversity in the offspring. During mutation in the genetic algorithm, each gene position in the chromosome is checked. With a mutation probability denoted as Pm, the gene is swapped with another gene in the same chromosome from the same chromosome.
4.3 Random swap operator
The random swap operator can improve the quality of offspring. Therefore, the following steps generate better offspring:
Step 1: To apply the random swap operator in the genetic algorithm, two groups of components are randomly selected from the pick chromosome, and a gene is randomly selected from each group to swapped. the same is done for the place chromosome.
Step 2: For the feeder chromosome, two gene positions are randomly selected, and they are swapped using the random operator.
Step 3: After applying the random swap operator, the offspring's fitness is evaluated. If the offspring's fitness exceeds that of the parent, the offspring is retained. Otherwise, the parent proceeds to the next iteration of the genetic algorithm.
5 Simulation experiment
In the experiment, the SMT machine uses four heads, with a spacing of 15 mm between heads and feeders. Parameters of the six PCBs used in the experiment are presented in Table 1. The algorithm was implemented in MATLAB 2019B and executed on a computer with a 2.4GHz processor and 8GB of RAM.
A random generation strategy was applied to generate component pick-and-place sequences, feeder placement sequences, and nozzle component allocation sequences for six PCBs. The process was repeated 100 times, and the shortest total movement distance was compared with the distances optimised using the proposed balanced distribution strategy and the Nearest Neighbour Algorithm, as shown in Table 2. In Table 2, Dss denotes the distance travelled by the nozzle across the feeder, Dpp represents the distance travelled by the nozzle on the PCB, Dpf represents the distance travelled by the nozzle between the feeder and the PCB, and Dis represents the total movement distance. BDS-NNA represents the combination of the balanced distribution strategy and the Nearest Neighbour Algorithm, RG denotes the random generation strategy, and Eff denotes the overall improvement efficiency.
Experimental results show that in the first stage, BDS-NNA outperforms the random generation strategy in terms of achieving shorter total movement distances. However, due to the complexity of PCB component layouts, optimisation efficiency varies significantly for different types of PCBs.
In the second stage of optimisation, the genetic algorithm population size is set to Q = 150. the maximum number of iterations is set as T=100, the crossover probability is set as Pc = 0.9, the mutation probability is set as Pm = 0.05, and the the number of local search iterations is NL = 4. To conduct a comparative analysis, the proposed Adaptive Crossover Genetic Algorithm (ACGA) introduced in this paper is compared with the MDFA algorithm from reference [6] and the MCGA algorithm from reference [20], under the same population sise and number of iterations.
The optimal distances for six PCBs are solved using three different algorithms each for 10 times. The average distance and the shortest distance obtained by each algorithm are presented in Table 3.
Based on Table 2, it can be observed that the Adaptive Crossover Genetic Algorithm (ACGA) reduced average distances by 4.15% and 7.02% for the placement of 6 PCBs compared to the MCGA and MDFA algorithms, respectively. Additionally, the ACGA algorithm achieved minimum distances that were 5.19% and 8.80% lower than that of the MCGA and MDFA algorithms, respectively.
Figures 6a and 6b illustrate the search progress of the three algorithms (ACGA, MCGA, and MDFA) for the 5th and 2nd PCBs, respectively, as shown in Table 3. In Figure 6a, ACGA achieved an optimal distance of 10,510 mm after 4,328 individual iterations, while MCGA reached the optimal distance of 11250mm after 4672 individual iterations, and MDFA obtained the optimal distance of 11440mm after 4866 individual iterations. In Figure 6b, ACGA achieved the optimal distance of 8380mm after 1700 individual iterations, MCGA reached the optimal distance of 8645mm after 2115 individual iterations, and MDFA obtained the optimal distance of 9063mm after 1970 individual iterations. These results indicate that the ACGA algorithm provides greater solution accuracy and faster convergence compared to the MCGA and MDFA algorithms.
Parameters of the 6 PCBs.
Comparison between BDS-NNA and the Random Generation Strategy.
Comparative Performance of Algorithms.
 |
Fig. 6 Performance comparison of the three algorithms: (a) The fifth PCB; (b) The second PCB. |
6 Conclusions
This paper has utilised the features of multi-head gantry-type SMT machines to propose an efficient method for initial solution generation based on the Balanced Distribution Strategy and Nearest Neighbour Algorithm as heuristics, aimed at reducing the time required for distance optimisation in the algorithm. Additionally, an adaptive crossover operator was introduced to further improve the speed and accuracy of the genetic algorithm. The proposed ACGA algorithm has been tested on six types of PCBs. Experimental results show that the ACGA algorithm proposed in this study achieved an average improvement in efficiency of 7.02% compared to the MDFA algorithm, and an average efficiency improvement of 4.15% compared to the MCGA algorithm. In future research, future work will explore optimisation for dual gantry-type surface mount machines and the load optimisation problem of multiple surface mount machines.
Funding
This research received no external funding.
Conflicts of interest
The authors have nothing to disclose.
Data availability statement
This article has no associated data generated and/or analyzed.
Author contribution statement
Zhiqiang Song: Methodology, Validation, Software, Writing – Original Draft Preparation. Chunfu Zhang: Conceptualization, Resources, Supervision, Funding Acquisition.
References
- T. He, D. Li, S.W. Yoon, A Heuristic Algorithm to Balance Workloads of High-speed SMT Machines in a PCB Assembly Line, Procedia. Manuf. 11, 1790–1797 (2017) [CrossRef] [Google Scholar]
- Q. Pi et al., Finite Potential Game Heuristic Algorithm for Workload Allocation in Dual-Gantry Placement Machines, IEEE Trans. Industr. Inform. 21, 2064–2073 (2025) [CrossRef] [Google Scholar]
- M. Castellani, S. Otri, D. T. Pham, Printed circuit board assembly time minimisation using a novel Bees Algorithm, Comput. Ind. Eng. 133, 186–194 (2019) [CrossRef] [Google Scholar]
- H.-P. Hsu, S.-W. Yang, Optimisation of component sequencing and feeder assignment for a chip shooter machine using shuffled frog-leaping algorithm, IEEE Trans. Autom. Sci. Eng. 17, 56–71 (2019) [Google Scholar]
- J. Mumtaz, Z. Guan, L. Yue, L. Zhang, C. He, Hybrid spider monkey optimisation algorithm for multi-level planning and scheduling problems of assembly lines, Int. J. Prod. Res. 58, 6252–6267 (2020) [CrossRef] [Google Scholar]
- H.-P. Hsu, Printed circuit board assembly planning for multi-head gantry SMT machine using multi-swarm and discrete firefly algorithm, IEEE Access. 9, 1642–1654 (2020) [Google Scholar]
- Y. Chen, J. Zhong, J. Mumtaz, S. Zhou, L. Zhu, An improved spider monkey optimisation algorithm for multi-objective planning and scheduling problems of PCB assembly line, Exp. Syst. Appl. 229, 120600 (2023) [CrossRef] [Google Scholar]
- C.-J. Lin, C.-H. Lin, Using an improved differential evolution for scheduling optimisation of dual-gantry multi-head surface-mount placement machine, Mathematics. 9, 2016 (2021) [CrossRef] [Google Scholar]
- H.-P. Hsu, Solving the feeder assignment, component sequencing, and nozzle assignment problems for a multi-head gantry SMT machine using improved firefly algorithm and dynamic programming, Adv. Eng. Inform. 52, 101583 (2022) [CrossRef] [Google Scholar]
- G. Lu, X. Yu, H. Sun, Z. Li, J. Qiu, H. Gao, A scan-based hierarchical heuristic optimisation algorithm for PCB assembly process, IEEE Trans. Ind. Informat. 20, 3609–3618 (2024) [CrossRef] [Google Scholar]
- G.-Y. Zhu, X.-W. Ju, W.-B. Zhang, Multi-objective sequence optimisation of PCB component assembly with GA based on the discrete Fréchet distance, Int. J. Prod. Res. 56, 4017–4034 (2018) [CrossRef] [Google Scholar]
- Z.k. Li, H. Sun, X. Yu, W. Sun, Heuristic sequencing hopfield neural network for pick-and-place location routing in multi-functional placers, Neurocomputing. 472, 35–44 (2022) [CrossRef] [Google Scholar]
- Y. Huang, L. Zhao, P. Liu, Feeder Layout Optimisation and Feeding Sequence Optimisation in High Speed and High Precision Placement Machine, Journal of Physics: Conference Series, Hangzhou,China, 2020, vol. 1605, no. 1, p. 012030. [CrossRef] [Google Scholar]
- T. He, D. Li, S.W. Yoon, A multi-phase planning heuristic for a dual-delivery SMT placement machine optimisation, Robot. Comput. Integr. Manuf. 47, 85–94 (2017) [CrossRef] [Google Scholar]
- D. Li, T. He, S.W. Yoon, Clustering-based heuristic to optimise nozzle and feeder assignments for collect-and-place assembly, IEEE Trans. Autom. Sci. Eng. 16, 755–766 (2018) [Google Scholar]
- T. He, D. Li, S.W. Yoon, An adaptive clustering-based genetic algorithm for the dual-gantry pick-and-place machine optimisation, Adv. Eng. Inform. 37, 66–78 (2018) [CrossRef] [Google Scholar]
- J. Zhong, Y. Chen, J. J. E. P. Mumtaz, A Multi-Objective Scheduling Optimisation Method for PCB Assembly Lines Based on the Improved Spider Monkey Algorithm, Eng. Proc. 23, 15 (2022) [Google Scholar]
- Q. Liu, X. Li, L.J.J.O.I.M. Gao, Mathematical modeling and a hybrid evolutionary algorithm for process planning, J. Intell. Manuf. 32, 781–797 (2021) [CrossRef] [Google Scholar]
- H. Gao, Z. Li, X. Yu, J. J.I.T.O.C. Qiu, Hierarchical multiobjective heuristic for PCB assembly optimisation in a beam-head surface mounter, IEEE Trans. Cybern. 52, 6911–6924 (2021) [Google Scholar]
- H. Wu, K. Wang, L. Ni, Minimal criterion genetic algorithm for multi-head surface mounting machine scheduling, Mod. Manuf. Eng. 3, 14–20 (2020) [Google Scholar]
Cite this article as: Zhiqiang Song, Chunfu Zhang, Multi-head surface mounting placement optimization based on adaptive multi-point crossover operator, Int. J. Simul. Multidisci. Des. Optim. 16, 8 (2025), https://doi.org/10.1051/smdo/2025007
All Tables
All Figures
 |
Fig. 1 Architectural diagram of a gantry-type SMT machine. |
| In the text | |
 |
Fig. 2 Nozzle Component Allocation Diagram :(a) arranging the components of each type in descending order based on their quantities ; (b)-(c) NZ4 components, having the lowest quantity are mounted first, followed by assigning the most numerous NZ5 components to nozzle H4 ; (d)-(e) Simulated placement continues until all components of types NZ3, NZ5, and NZ6 are placed ; (f) If there are no remaining unassigned component types and the difference in component quantities among the nozzles does not exceed 2, the simulated mounting process is terminated. |
| In the text | |
 |
Fig. 3 Feeder Arrangement Diagram. |
| In the text | |
 |
Fig. 4 The flowchart of the Nearest Neighbour Algorithm. |
| In the text | |
 |
Fig. 5 Illustration of the adaptive crossover operator: (a) In the early stages of iteration, perform a 4-point crossover on the parent chromosomes; (b) Offspring generated from the 4-point crossover; (c) In the later stages of iteration, perform a 2-point crossover on the parent chromosomes; (d) Offspring generated from the 2-point crossover. |
| In the text | |
 |
Fig. 6 Performance comparison of the three algorithms: (a) The fifth PCB; (b) The second PCB. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




