EDP Sciences logo
Submit your paper
Search
Menu
Home All issues Volume 12 (2021) Int. J. Simul. Multidisci. Des. Optim., 12 (2021) 12 Full HTML
Issue
Int. J. Simul. Multidisci. Des. Optim.
Volume 12, 2021
Computation Challenges for engineering problems
Article Number 12
Number of page(s) 9
DOI https://doi.org/10.1051/smdo/2021014
Published online 13 August 2021

© P. Rakesh and B. Pal, Published by EDP Sciences, 2021

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

Ti6Al4V alloy is a commonly used biomaterial for load-bearing orthopedic implants [1]. Solid Ti6Al4V has an elastic modulus around 110 GPa, much higher than those of the natural bones [2]. The difference of elastic modulus between a solid Ti6Al4V implant and the adjacent bone causes stress-shielding, leading to implant loosening [3]. To avoid the risk of implant loosening, the implants should ideally be developed with comparable mechanical properties to those of natural bones. Metallic porous implants and porous structures have been investigated in the literature to reduce the problems associated with stiffness mismatch of the implants and optimize porous structure designs [4–11]. The mechanical properties of porous structures and their biological behavior, such as cell attachment and tissue growth, depend on the structural parameters of the porous structure, including the unit cell type, porosity, and pore size [12]. The combination of suitable material, the geometry of the porous structure, and optimum structural parameters reduces the implant stiffness and overcomes the effect of stress-shielding [13]. It is reported that the porosity of a porous implant should be more than 50% to promote bone ingrowth [14,15]. However, too large a pore size affects the load-bearing capacity.

Depending on the pore types, porous structures are classified as closed pores and open pores [16]. Based on the arrangement of the unit cell, the structures may be classified as stochastic and non-stochastic [17]. In stochastic structures, the unit cells are irregularly arranged. However, stochastic porous implants show large deformation [18]. The non-stochastic or periodic cellular structures are built-in regular form and have higher mechanical properties [19]. These are commonly designed based on three-dimensional (3D) unit cells such as diamond lattice [20], Body-centered-cubic (BCC) [5,8], face-centered-cubic (FCC) [4], Tetrahedron cell, and Octet truss cell [5]. Using Finite Element Analysis (FEA), previous studies have analyzed the mechanical behavior of different porous structures under different loading conditions, and the results were consistent when compared with the experimental results [5–9]. Cubic porous structures with different porosities were fabricated using an additive manufacturing process with biocompatible materials [6,7,9]. Under compression loading, the effective stiffness and compressive strength values were reported to decrease with increasing porosity. Consistent stress distribution was reported in each strut of the porous Cubic structure, but mechanical properties were reported to vary with variable struct thickness [6,7].

Research has been conducted on BCC porous structures aiming to develop a methodology for deriving the theoretical porosity of BCC structure by relating the structural parameters [5,8]. In the study by Wang et al. [8], BCC porous Ti6Al4V samples were manufactured via 3D printing and subsequently tested mechanically. It is reported that porous structures can lower the effective elastic modulus of implants considerably. Wang et al. [5] investigated the cell proliferation on BCC porous hip stem. Their study reported that the cell proliferation rate for a porous structure was 140% during the first 4–7 days, while it was only 90% with the uniform structures. Hassan et al. [9] investigated the orientations of the internal strut of Cubic, Diamond, and BCC porous structures. As reported in their study, the BCC structures demonstrated relatively isotropic mechanical properties under multiple loading conditions compared to the Diamond and Cubic structures.

Low porosity offers good mechanical strength but a reduced opportunity for bone ingrowth by promoting pore occlusion [14,15]. Furthermore, investigation on open-cell Spherical porous structures was scarce in the literature. In the current study, Ti6Al4V porous structures were designed and analyzed under compressive displacement by considering 2% strain to determine the mechanical behavior of the porous structures (with porosity more than 60%) for application on a low-stiff hip implant. Three different pore types, namely BCC, Cubic, and Spherical type, were considered. Each type of porous structure was modeled for four different porosities. Finite Element (FE) results were compared with the analytical calculations based on Gibson and Ashby method for validation. The specific objectives of the current study are to (i) investigate and compare the mechanical behaviors of the BCC and Cubic porous structures under compressive displacement, (ii) establish the ideal porosity range of such structures that can mimic the mechanical properties of the natural bone, and (iii) explore the feasibility of the open-cell Spherical porous structure for implant application.

2 Materials and methods

2.1 Design of porous structures

3D CAD models of three types of porous structures (BCC, Cubic, and Spherical) were designed using SolidWorks software (Dassault Systemes, MA, USA). The overall size of the porous structure was 15 mm × 15 mm ×15 mm3, chosen according to the ISO standard 13314:2011. It was reported that the porosity of the porous implants should be greater than 50% [14,15]. In the current study, the porosity was varied from 67% to 82%. For each type of porous structure, four different porosities (67%, 70%, 76%, and 82%) were modeled with variable strut sizes and pore sizes of the unit cell. The porosity of the porous structures was calculated based on the volume fraction of the porous structure [6,7] by using the following equation.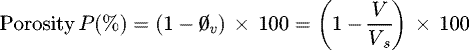(1)

P is the porosity and ∅v is the volume fraction. ‘V’ is the volume of the Ti6Al4V porous structure, and Vs is the volume of the Ti6Al4V solid structure.

The BCC(82), BCC(76), BCC(70), and BCC(67) models were designed with a unit cell size ‘a’ equal to 2.1428 mm (constant), inner strut diameter ‘Di’, outer strut diameter ‘Do’ and variable pore size ‘b’, as listed in Table 1. The inner and outer struts are oriented in [0° ± 45° ± 90°] with each other, as shown in Figure 1a. The CAD models of the Cube(82), Cube(76), Cube(70), and Cube(67) were designed by varying strut size from 0.5 mm to 0.7 mm and pore size from 1.5714 mm to 1.3314 mm within a unit cell, as listed in Table 1. For the Cubic models, the struts were arranged in [0° ± 90°] to each other, as shown in Figure 1b. The CAD models of Spherical(82), Spherical(76), Spherical(70), and Spherical(67) were designed, as shown in Figure 1c, by varying pore diameter from 1.80 mm to 1.514 mm (Tab. 1). The distance between the adjacent pores was maintained as 0.3 mm for 82% porosity, 0.4 mm for 76% porosity, 0.5 mm for 70%, and 0.55 mm for 67% within a unit cell. The 3D CAD models of the BCC(82), Cubic(82), and Spherical(82) porous structures are shown in Figure 2a–c. All the CAD models of the various porous structures were exported to ANSYS for further development and analysis of the models.

Table 1

The dimensions of individual components of the BCC, Cubic, and Spherical porous structures.

thumbnail Fig. 1

The geometry of the unit cell of the porous structures; (a) BCC unit cell, (b) Cubic unit cell, (c) Spherical unit cell.
thumbnail Fig. 2

3D CAD models of the 82% porous structures; (a) BCC porous structure, (b) Cubic porous structure, (c) Spherical porous structure.

2.2 FE modeling porous structures

The 3D CAD models of Cubic, Spherical, and BCC porous designs were imported to ANSYS Workbench 16.0 (Ansys, PA, USA). The models were meshed using 10-noded tetrahedral elements with 0.1 mm of the mesh size. Mesh sensitivity analysis was performed on each model. The models were initially discretized with 0.1 mm and 0.2 mm mesh sizes. It was observed that the difference in stresses and strain values between these models is less than 2%. The models with 0.1 mm mesh size were selected for subsequent analysis. As an example, the FE model of the Cubic(76) porous structure is shown in Figure 3. The elastic-plastic (bilinear) material properties of Ti6Al4V alloy were attributed to the model, with an elastic modulus of 110 GPa, Poisson ratio of 0.3, yield strength of 930 MPa, and tangent modulus of 1.25 GPa [2]. Compressive displacement of 0.32 mm was applied (axial y-direction) on the top face of each model by considering 2% of strain [9], whereas the bottom face was constrained for all degrees of freedom (Fig. 4).

Similar to Hassan et al. [9], the effective elastic modulus (Eeff) was calculated from Hooke's law as expressed by equation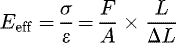 (2).(2)

where σ is stress, ϵ is strain, F is the reaction force, A is the area, ΔL is the change in length, and L is the original length of the porous structure. Original length is the length of the cube is L = 15 mm. Change in length is equal to deformation in the model under compressive loading conditions.

thumbnail Fig. 3

FE model of the Cubic (76) porous structure.
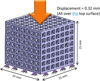thumbnail Fig. 4

Loading and boundary conditions applied on the Cubic (76) porous structure (similar loading and boundary conditions were applied to the BCC and Spherical porous structure models).

2.3 Gibson and Ashby method-based calculations for validation

The analytical method developed by Gibson and Ashby [16] has been used in the literature to evaluate the material properties of porous structures, including Ti-alloys for orthopedic applications [5–8]. A good agreement was reported between analytical and experimental results as well as simulated FEA results. To validate the current FE models, the simulation results were compared with the values obtained from the model proposed by Gibson and Ashby [16]. The Gibson and Ashby model used a power function to evaluate the effective elastic modulus and yield strengths of the porous structures, as shown by equations (3) and (4).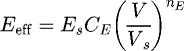(3) (4)

Eeff and Sy are the effective elastic moduli and yield strengths of the porous structures, respectively. Es and Ss are the elastic modulus and yield strength of bulk Ti6Al4V alloy, respectively. V is the volume of the porous structure and Vs is the volume of the solid Ti6Al4V. CE and nE are the coefficients to determine the effective elastic moduli, and Cy and ny are the coefficients to determine the effective yield strengths of porous structures [9]. FEA results of the effective elastic modulus and effective yield strength were plotted for all the volume fractions, and the best-fit curves were established in the form of the Gibson-Ashby power function using the regression tool. The coefficients and the equations relating the effective mechanical properties and the volume fractions were thus obtained. The Gibson-Ashby effective elastic modulus and the effective yield strength were then calculated using the coefficients obtained through regression.

3 Results

Reaction force and directional maximum deformation data (in the direction of applied displacement) were obtained from the FE simulations and used for calculating the stress and strain. The reaction force versus directional deformation diagrams was plotted for all the porous models. As an example, the reaction force versus deformation diagram is presented in Figure 5 for the Cubic porous structures. The stress–strain diagrams (Fig. 6a–c) were then plotted for all the models. An elastic-plastic behavior was found for all the porous structures. The effective elastic modulus and yield strength under compression were calculated from these stress-strain diagrams for all the porous models. The effective elastic modulus was obtained by calculating the slope of the linear part of the stress-strain diagrams. The effective yield strength was calculated using 0.2% offset method. As an example, Figure 7 shows the measurement of the effective elastic modulus and compressive yield strength. The calculated results for all the models are summarized in Table 2. Results show that the effective elastic modulus and yield strength of BCC, Cubic, and Spherical porous structures decrease with increasing pore size and porosity and decreasing strut size (Fig. 8a,b). The effective elastic moduli of the Cubic and Spherical porous structures were found to range from 18.52 GPa to 29.03 GPa and from 13.94 GPa to 27.66 GPa, respectively, when the porosity was varied from 82% to 67% (Tab. 2). The effective yield strengths were found to range from 142.3 MPa to 219.01 MPa and from 59.99 MPa to 158.51 MPa, respectively, when the porosity was varied from 82% to 67% (Tab. 3). The Spherical porous structures of 70% and 67% porosities seemed to deform much at small loads, as shown in Figure 9. Similar to the Cubic and Spherical porous structures, the effective elastic modulus and yield strength of the BCC porous structures were found to increase with decreasing porosity and strut size (outer and inner strut) as well as increasing pore size (Fig. 8, Tabs. 2 and 3). The effective elastic modulus of BCC porous structures ranged from 16.757 GPa to 24.529 GPa (Tab. 2) when the porosity was varied from 82% to 67%. Similarly, the yield strength was found to vary between 133.25 MPa to 196.25 MPa (Tab. 3) when the porosity was varied from 82% to 67%. Results show that the effective elastic modulus and yield strength values of Cubic porous structures were higher than those of the Spherical and BCC porous structures.

thumbnail Fig. 5

Reaction force − directional deformation curves of the Cubic porous structures with four different porosities.
thumbnail Fig. 6

Stress–strain curves obtained using the FE analysis of porous structures with different porosities; (a) BCC, (b) Cubic, and (c) Spherical.
thumbnail Fig. 7

Yield strength by 0.2% offset method and effective elastic modulus of Cubic (82) model (similar method applied to all porous structures).
thumbnail Fig. 8

(a) Effective elastic modulus-porosity curves of BCC, Cubic, and Spherical porous structures of four different porosities, (b) effective yield strength − porosity curves of BCC, Cubic, and Spherical porous structures of four different porosities.
thumbnail Fig. 9

Deformed Spherical porous structure of 70% porosity (similar behavior also observed for 67% porosity).

3.1 Validation of FE models

The results were compared with the numerical values predicted by Gibson and Ashby method. The best-fit power function that describes the relationship between the relative elastic modulus and volume fraction and the relative yield strength and volume fraction were obtained by regression technique (Fig. 10a, b). The different values of the coefficients obtained for all the porous designs are reported in Tables 2 and 3. For the Cubic porous structures, the values are CE = 0.6159, nE = 0.7458 and Cy = 0.522, ny = 0.7011. For the BCC porous structure, CE = 0.5037, nE = 0.7271 and Cy = 0.4782, ny = 0.7306 and for the Spherical porous structure CE = 0.911, nE = 1.133 and Cy = 1.0605, ny = 1.6068. Using these coefficients, the effective elastic modulus and yield strength values were calculated using the Gibson-Ashby model (Eqs. (3) and (4)) for all porosities (67–82%) of the Ti6Al4V porous structures (Tabs. 2 and 3). The effective elastic modulus of the BCC porous structures varied between 16.57 and 24.37 GPa, and the yield strength varied between 132.18 and 194.85 MPa. Whereas the effective elastic modulus of the Cubic porous structures varied between 18.55 and 28.96 GPa, and the yield strength varied between 143.71 and 218.42 MPa. For the Spherical porous structures, the effective elastic modulus varied between 13.94 and 27.74 GPa, and the yield strength varied between 60.15 and 159.5 MPa. The effective mechanical properties obtained by the Gibson and Ashby model closely matched the FEA results, as shown in Tables 2 and 3.

thumbnail Fig. 10

Best-fit power functions (a) relative effective elastic modulus-volume fractions curves of BCC, Cubic, and Spherical porous structures, (b) relative effective yield strength-volume fractions curves of BCC, Cubic, and Spherical porous structures.

4 Discussion

Using FE analysis, this study aimed at establishing the ideal porosity range of Ti6Al4V porous structures for applications on hip implants. Mechanical behavior of the BCC and Cubic porous structures were investigated and compared to those reported in the literature. Investigation on open-cell Spherical porous structures was scarce. The study additionally explored the feasibility of the Spherical porous structure for hip implant application. BCC, Cubic, and Spherical porous structures of Ti6Al4V alloy with four different porosities (ranging from 67% to 82%) were designed by varying the pore size and strut size. The effective mechanical properties of the porous structures under compressive displacement (0.32 mm) were evaluated. The results show that the effective mechanical properties of the BCC and Cubic porous structures modeled in this study are in the range of the properties of cortical bone and suitable for porous hip implant application. The open-cell Spherical porous structure was found not suitable.

The compressive stress-strain curves of the BCC, Cubic, and Spherical porous structures of Ti6Al4V alloy of all four porosities were shown in Figure 6. For all the models, the transition of the stress-strain curves from linear to the non-linear region was observed at a load higher than the maximum load on the hip joint (11000 N) during stumbling [21] (Fig. 5). The elastic modulus was calculated from the slope of the linear part of the stress–strain curve. By using 0.2% offset method, the compressive yield strength was measured from the stress–strain curves of Ti6Al4V porous structures (Fig. 7). It was observed that the effective elastic modulus and yield strength of BCC, Cubic, and Spherical porous structures decrease with increasing pore size and porosity (Fig. 8). This trend was similar to that reported in the literature [6–9]. Such changes in mechanical properties are justified as the mechanical properties of porous structures depend on the geometry of the structure, including the shape and size of the cells, distribution of material between the cell edges and faces, and the relative density or porosity [16]. For each specific type of porous structure, the reduction in porosity led to the reduction of the effective mechanical properties of the structures. As reported in Tables 2 and 3, the effective elastic moduli of the Cubic porous structures of 82%, 76%, 70%, and 67% porosities are 18.52 GPa, 23.41GPa, 26.87 GPa, and 29.03 GPa and the yield strengths are 142.3 MPa, 177.6 MPa, 205.4 MPa, and 219 MPa, respectively. These values are in the range of elastic modulus (7 to 30 GPa) and yield strength (100 to 230 MPa) properties of the cortical bone [22]. The effective elastic moduli of the BCC porous structure of 82%, 76%, 70%, and 67% porosities are 16.757 GPa, 19.59 GPa, 22.98 GPa, and 24.52 GPa and yield strengths are 133.25 MPa, 158 MPa, 182.5 MPa, and 196.2MPa, respectively (Tabs. 2 and 3). These values are also in the range of the elastic modulus (7 to 30 GPa) and yield strength (100 to 230 MPa) properties of the cortical bone [22]. It may be commented that the Cubic and BCC porous structures of all the porosities modeled in this study are suitable for low-stiff hip implant application.

The effective elastic moduli of the Spherical porous structure of 82%, 76%, 70%, and 67% porosities are 13.94 GPa, 18.95 GPa, 24.81 GPa, and 27.66 GPa and the yield strengths are 59.99 MPa, 95.01 MPa, 135 MPa, and 158.51 MPa, respectively. While the effective elastic moduli of the Spherical porous structure of 82% and 76% porosities are within the range of the cortical bone, yield strengths are not in the range of the cortical bone. Again, the effective elastic moduli and yield strengths of 70% and 67% porosities of Spherical porous structures are within the range of the cortical bone properties, but the struts of porous structures seemed to deform considerably at small loads (Fig. 9). Those loads were found to be smaller than the maximum load on the hip joint 11000 N during stumbling [21]. Therefore, based on the results of the current study, the Spherical porous structures seem to be unsuitable for porous implant design applications.

The Cubic porous structures yielded the highest effective elastic modulus and yield strengths compared with the Spherical and BCC structures for all four porosities modeled in this study (Tabs. 2 and 3). The Spherical porous structures provided the least effective elastic moduli and yield strength for the same porosities. Similar to the study by Mehboob et al. [9], the effective elastic moduli and yield strengths values of the BCC porous structures are nearer to those of the Cubic porous structures. Therefore, it can be said that the mechanical properties of porous structures depend on porosity, the geometry of porous structures, and structural parameters.

The results obtained using the Gibson-Ashby method were used for validating the FE results. The Gibson-Ashby coefficients were obtained through regression of the effective mechanical properties (FEA) and the volume fractions (Fig. 10a, b). The effective elastic modulus versus volume fraction values of the BCC, Cubic, and Spherical porous structures were found to correlate well. The coefficients of determination (R 2) values were observed as 0.9894, 0.9993, and 0.9999, respectively, for the BCC, Cubic, and Spherical porous structures (Fig. 10a). Similar to the effective elastic modulus, the effective yield strength versus volume fraction values of the BCC, Cubic, and Spherical porous structures were also well fitted to the power function. The coefficients of determination (R 2) values were observed as 0.9955, 0.9988, and 0.999, respectively, for BCC, Cubic, and Spherical porous structures (Fig. 10b). Therefore, it can be commented that the mechanical properties of the Ti6Al4V porous structures (all types) correlate well with the volume fractions. Using the values of the Gibson-Ashby coefficients, theoretical values of the effective elastic modulus and yield strength were calculated (Tabs. 2 and 3). It is observed that the results of the Gibson and Ashby model closely matched the FEA results, indicating the validity of the FE models. Only negligible differences in results were observed for BCC, Cubic, and Spherical porous structures for the different porosities modeled in this study. Such a small discrepancy may be justified because of the ability of the Gibson-Ashby model to predict the effective elastic moduli of porous structures with porosities of 60% and above [5–9, 12–16].

For the BCC and Cubic porous structures, the results obtained from FEA and the Gibson-Ashby method and their variation with the changing porosity were found to be consistent with published studies [6,8–9]. Effective yield strength of Cubic porous structures with 67% to 82% porosity was approximately in the range of those reported by Parthasarathy et al. [6] and Mehboob et al. [9]. Also, the effective mechanical properties of BCC(82) porous structures were close to 80% porosity of the BCC porous model of Wang et al. [8]. The small differences observed in the values for the effective elastic modulus, however, may be because of different overall dimensions of the porous structures in their studies. An attempt was made to compare the results to those reported by Abdualaziz et al. [23], who investigated the mechanical properties of Ti6Al4V Spherical porous structures but with lower porosities (0–55%). The results are not meaningfully comparable as the modeled porosities are different. However, the observed discrepancy in the results of the current study was less than that reported in [23].

This study has described the design and analysis of different geometries of porous structures to evaluate their mechanical properties for the application of low-stiff hip implants. However, the study has some limitations. The models have been investigated only under compressive displacement. Future work will be needed to investigate the mechanical properties under other types of loading conditions to understand the behavior of the porous structures fully. Porous structures of other pore types should also be investigated. The fatigue strength of porous structures was not evaluated in the current study. Moreover, further investigations will be required to quantify the mechanical properties of the 3D printed porous structures.

Table 2

FEA and Gibson-Ashby effective elastic moduli of all porous structures with different porosities.

Table 3

FEA and Gibson-Ashby yield strengths of all porous structures with different porosities.

5 Conclusions

BCC, Cubic, and Spherical porous structures with four different porosities were designed and analyzed using FEA under compressive displacement. The effective elastic modulus and yield strength were found to decrease with an increase in porosity and pore size of the porous structures. The effective elastic modulus and yield strength of 82%, 76%, 70%, and 67% porous BCC and Cubic porous structures are in the range of elastic modulus and yield strength properties of the cortical bone. These values also compared well with Gibson and Ashby method-based calculations. Therefore, the modeled porosities of the BCC and Cubic are suitable for hip implant application. Spherical porous structures may not be suitable for implant application because the struts deformed at a compressive load smaller than the maximum loads on the hip joint. None of the porous designs was found ideal for trabecular bone applications.

Acknowledgments

Porika Rakesh thankfully acknowledges the postgraduate scholarship (MHRD, Govt. of India) received during his postgraduate study.

References

  1. H.J. Rack, J.I. Qazi, Titanium alloys for biomedical applications, Mater. Sci. Eng. C 26, 1269–1277 (2006) [CrossRef] [Google Scholar]
  2. W. Ziaja, Finite element modeling of the fracture behavior of surface treated Ti6Al4V alloy, Arch. Comput. Mater. Sci. Surf. Eng. 1, 53–60 (2009) [Google Scholar]
  3. D.R. Sumner, Long-term implant fixation and stress-shielding in total hip replacement, J. Biomech. 48, 797–800 (2015) [CrossRef] [Google Scholar]
  4. M. Alaña, A. López de Arancibia, A. Pradera-Mallabiabarrena, S. Ruiz de Galarreta, Analytical model of the elastic behavior of a modified face-centered cubic lattice structure, J. Mech. Behav. Biomed. Mater. 98, 357–368 (2019) [CrossRef] [Google Scholar]
  5. S. Wang, L. Liu, L. Kai, L. Zhua, J. Chen, Y. Hao, Pore functionally graded Ti6Al4V scaffolds for bone tissue engineering application, Mater. Des. 168, 107643 (2019) [CrossRef] [Google Scholar]
  6. J. Parthasarathy, B. Starly, S. Raman, A. Christensen, Mechanical evaluation of porous titanium (Ti6Al4V) structures with electron beam melting, J. Mech. Behav. Biomed. Mater. 3, 249–259 (2010) [CrossRef] [Google Scholar]
  7. K. Hazlehurst, C.J. Wang, M. Stanford, Evaluation of the stiffness characteristics of square pore CoCrMo cellular structures manufactured using laser melting technology for potential orthopedic applications, Mater. Des. 51, 949–955 (2013) [CrossRef] [Google Scholar]
  8. L. Wang, J. Kang, C. Sun, D. Li, Y. Caoa, Z. Jin, Mapping porous microstructures to yield desired mechanical properties for application in 3D printed bone scaffolds and orthopedic implants, Mater. Des. 133, 62–68 (2017) [CrossRef] [Google Scholar]
  9. H. Mehboob, F. Tarlochan, A. Mehboob, S.H. Chang, Finite element modeling and characterization of 3D cellular microstructures for the design of cement less biomimetic porous hip stem, Mater. Des. 149, 101–112 (2018) [CrossRef] [Google Scholar]
  10. J.-H. Zhu, K.-K. Yang, W.-H. Zhang, Backbone cup − a structure design competition based on topology optimization and 3D printing, Int. J. Simul. Multisci. Des. Optim. 7, A1 (2016) [CrossRef] [Google Scholar]
  11. R. Paz, M.D. Monzón, B. González, E. Pei, G. Winter, F. Ortega, Lightweight parametric optimisation method for cellular structures in additive manufactured parts, Int. J. Simul. Multisci. Des. Optim. 7, A6 (2016) [CrossRef] [Google Scholar]
  12. L. Mullen, R.C. Stamp, W.K. Brooks, E. Jones, C.J. Sutcliffe, Selective laser melting: a regular unit cell approach for the manufacture of porous, titanium, bone in‐growth constructs, suitable for orthopedic applications, J. Biomed. Mater. Res. B 89, 325–334 (2009) [CrossRef] [Google Scholar]
  13. S. Kujala, J. Ryhänen, A. Danilov, J. Tuukkanen, Effect of porosity on the osteointegration and bone ingrowth of a weight-bearing nickel-titanium bone graft substitute, Biomaterials 24, 4691–4697 (2003) [CrossRef] [Google Scholar]
  14. S. Arabnejad, R.B. Johnston, J.A. Pura, B. Singh, M. Tanzer, D. Pasini, High-strength porous biomaterials for bone replacement: a strategy to assess the interplay between cell morphology, mechanical properties, bone ingrowth and manufacturing constraints, Acta Biomater. 30, 345–356 (2016) [CrossRef] [Google Scholar]
  15. N. Taniguchi, S. Fujibayashi, M. Takemoto, K. Sasaki, B. Otsuki, T. Nakamura, T. Matsushita, T. Kokubo, S. Matsuda, Effect of pore size on bone ingrowth into porous titanium implants fabricated by additive manufacturing: an in vivo experiment, Mater. Sci. Eng. C 59, 690‒701 (2016) [Google Scholar]
  16. L.J. Gibson, M.F. Ashby, Cellular Solids: Structure and Properties Textbook, Cambridge University Press (1997) [Google Scholar]
  17. X.P. Tan, Y.J. Tan, C.S.L. Chow, S.B. Tor, W.Y. Yeong, Metallic powder-bed based 3D printing of cellular scaffolds for orthopedic implants: a state-of-the-art review on manufacturing, topological design, mechanical properties and biocompatibility, Mater. Sci. Eng. C 76, 1328–1343 (2017) [Google Scholar]
  18. S. Sogutlu, B. Koc, Stochastic modeling of tissue engineering scaffolds with varying porosity levels, Comput. Aided Des. Appl. 4, 661–670 (2007) [Google Scholar]
  19. O. Cansizoglu, D. Harrysson, O. Cormier, H. West, T. Mahale, Properties of Ti6Al4V non-stochastic lattice structures fabricated via electron beam melting, Mater. Sci. Eng. A 492, 468–474 (2008) [Google Scholar]
  20. S.M. Ahmadi, G. Campoli, S. Amin Yavari, B. Sajadi, R. Wauthle, J. Schrooten, H. Weinans, A.A. Zadpoor, Mechanical behavior of regular open-cell porous biomaterials made of diamond lattice unit cells, J. Mech. Behav. Biomed. Mater. 34, 106–115 (2014) [Google Scholar]
  21. G. Bergmann, A. Graichena, A. Rohlmann, B. Bender, G.N. Heinleina, M.O. Duda, M.M. Helle Morlock, Realistic loads for testing hip implants, Bio-Med. Mater. Eng. 20, 65–75 (2010) [Google Scholar]
  22. S. Mohamed, B. Halima Shamaz, Bone tissue engineering and bony scaffolds, Int. J. Dent. Oral Health 1, 15–20 (2015) [Google Scholar]
  23. A.S. Al-Aboodi, A.A. Al-Nasser, Bone porosity modeling and FE simulation, Int. J. Adv. Mech. Aeron. Eng. 2, (2015) [Google Scholar]

Cite this article as: Porika Rakesh, Bidyut Pal, Finite element analysis of Ti6Al4V porous structures for low-stiff hip implant application, Int. J. Simul. Multidisci. Des. Optim. 12, 12 (2021)

All Tables

Table 1

The dimensions of individual components of the BCC, Cubic, and Spherical porous structures.

In the text
Table 2

FEA and Gibson-Ashby effective elastic moduli of all porous structures with different porosities.

In the text
Table 3

FEA and Gibson-Ashby yield strengths of all porous structures with different porosities.

In the text

All Figures

thumbnail Fig. 1

The geometry of the unit cell of the porous structures; (a) BCC unit cell, (b) Cubic unit cell, (c) Spherical unit cell.
In the text
thumbnail Fig. 2

3D CAD models of the 82% porous structures; (a) BCC porous structure, (b) Cubic porous structure, (c) Spherical porous structure.
In the text
thumbnail Fig. 3

FE model of the Cubic (76) porous structure.
In the text
thumbnail Fig. 4

Loading and boundary conditions applied on the Cubic (76) porous structure (similar loading and boundary conditions were applied to the BCC and Spherical porous structure models).
In the text
thumbnail Fig. 5

Reaction force − directional deformation curves of the Cubic porous structures with four different porosities.
In the text
thumbnail Fig. 6

Stress–strain curves obtained using the FE analysis of porous structures with different porosities; (a) BCC, (b) Cubic, and (c) Spherical.
In the text
thumbnail Fig. 7

Yield strength by 0.2% offset method and effective elastic modulus of Cubic (82) model (similar method applied to all porous structures).
In the text
thumbnail Fig. 8

(a) Effective elastic modulus-porosity curves of BCC, Cubic, and Spherical porous structures of four different porosities, (b) effective yield strength − porosity curves of BCC, Cubic, and Spherical porous structures of four different porosities.
In the text
thumbnail Fig. 9

Deformed Spherical porous structure of 70% porosity (similar behavior also observed for 67% porosity).
In the text
thumbnail Fig. 10

Best-fit power functions (a) relative effective elastic modulus-volume fractions curves of BCC, Cubic, and Spherical porous structures, (b) relative effective yield strength-volume fractions curves of BCC, Cubic, and Spherical porous structures.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.