| 期号 |
Int. J. Simul. Multidisci. Des. Optim.
卷号 12, 2021
Computation Challenges for engineering problems
|
|
|---|---|---|
| 文献编号 | 6 | |
| 页数 | 6 | |
| DOI | https://doi.org/10.1051/smdo/2021005 | |
| 网上发表时间 | 2021年6月18日 | |
Research Article
R-tree data structure implementation for Computer Aided Engineering (CAE) tools
1
School of mechanical engineering, VIT University, Chennai campus, Chennai 600 127, India
2
Renault Nissan Technology Business Centre Pvt Ltd, Ascendas It Park, Mahindra World City, No. Tp 2/1, Natham Sub-post Office, Chengalpattu, Chennai 603002, India
* e-mail: vaibhavshelar100@gmail.com
Received:
11
January
2021
Accepted:
12
April
2021
Searching and handling geometric data are basic requirements of any Computer Aided Engineering application (CAE). Spatial search and local search has greater importance in CAD and CAE applications for reducing the model preparation time. There are many efficient algorithms being made to search geometrical data. Current neighbour search strategy is limited and not efficient in different CAE platforms. R-tree is tree data structure used for spatial access methods. This paper presents a review of R-tree data structure with its implementation in one of the CAE tool for neighbour search and local search. It satisfies current neighbour search requirements in CAE tools. Results shows considerable amount of time saving compared to the conventional approach. This work concludes that R-tree implementation can be helpful in identifying neighbour part and reducing model preparation time in CAD and CAE tools.
Key words: R-tree / CAD / CAE / geometrical data / local search / neighbour search
© V. Shelar et al., Published by EDP Sciences, 2021
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Finite element model preparation is one of the major time consuming and one of the important phase in the product development process, which includes geometric simplification, meshing and model connections. Mid-surface extraction and model connections are top two priority tasks in finite element modelling process. Dong-Pyoung Sheen and Tae-geun Son (2008) developed algorithm for mid-surface extraction [1]. In their algorithm to identify nearest pair face they used distance criteria which will not give exact near face. Most of the existing mid-surface algorithm require efficient near search to reduce searching time. Figure 1 shows neighbour search requirement in mid-surface extraction.
Different trials are performed in ANSA CAE1 pre-processing application for extracting mid-surface which shows current search process is not efficient and having limitations. Current process takes more time to identify nearest pair faces.
As shown in Figure 2 as number of faces are increased, the time grows exponentially. It indicates the searching is not efficient. For large model it is time consuming and does not work. For large assembly the model fails to give results.
Neighbour search is not only required in mid-surface extraction but also in model connections. Searching particular part in whole assembly and making manual connection is laborious. While creating model connections, neighbour search is essential. If one part is selected another parts which is nearest to selected part should get searched to facilitate the model connections. Model connections can be automated easily if one part is given as input and nearest part should get easily searched (Fig. 3).
These problems can be handled efficiently if nearest neighbour points, faces and surfaces are correctly identified. If all geometric data is well organised then it will quickly search the required entities. A perfect data structure needs to be implemented. There are basically three data structure available to organise data.
-
R-Trees
-
K-D Trees
-
Octree.
Guttman (1984) proposed R-tree to handle geometrical data, such as points, line segments, surfaces, volumes and hyper-volumes in high-dimensional spaces [2]. R-trees can handle range and topological queries. He further concluded that, R-trees are also used to handle the queries related to directions. Roussopoulos (1995) introduced to handle the problem of answering k nearest-neighbour (NN) queries using R-trees [3]. Manolopoulos (2013) has explained briefly query processing for Range, topological, directional and nearest neighbour queries [4]. The basic requirements for efficient searching is to handle multidimensional data. Mamoulis and Wong (2013) have done survey on multidimensional access methods [5]. R trees can handle multidimensional data efficiently.
They concluded that, each data structure has its pros and cons depending on their applications [5]. K-D Trees are not suitable for high dimensional space [6]. Patel (2013) did comparison of advanced data structures [7]. He concluded that, octree data structure is usually unbalanced. R-tree data structure is always balanced [8]. It indicates R-trees has wide applications due to its more efficient access. R-tree approach is suitable for mentioned problems as it fulfills current search requirements.
 |
Fig. 1 Neighbour search requirement for mid-surface extraction. |
 |
Fig. 2 Time study for conventional approach. |
 |
Fig. 3 Neighbour search requirement for connections. |
2 Methods
R-Trees can organize any-dimensional data by representing the data by a minimum bounding box. Each node bounds its children. Leaf nodes of the R-tree contain entries of the form (RECT; oid) where ‘oid’ is an object-identifier and is used as pointer to a data object and RECT is an n-dimensional Minimal Bounding Rectangle (MBR) which bounds the corresponding object. For example, in a 2-dimensional space, an entry RECT will be of the form (x low; x high; y low; y high) which represents the coordinates of the lower-left and upper-right corner of the rectangle. This work makes an effort to use R-Tree for efficient search (Fig. 4).
As an example a full car assembly is taken and as shown in Figure 5 which contain more complex geometric data. It shows 2-D representation of R-tree methodologyfor full car assembly.
Full car assembly contain large number of parts and contain more geometric data. If user wants to search tire part in whole assembly. R-tree is built by rectangles for all parts in assembly. Query rectangle is formed as R16 which contain tire part. To query R-tree, starting at the root, examine each child node, and check if it intersect or contained by the rectangle being queried for. Here query rectangle is contained by R2. So it will recurs into the R2 only. R2 has child nodes R5 and R6. Again query rectangle R16 is contained by R6. At leaf node, it will check each entry to see if it intersects or contain with the query area, and return it if it does. Final search result will be R16 which will show the desired tire part. Similarly it can be implemented for other geometrical and elemental data.
 |
Fig. 4 R-tree algorithm. |
 |
Fig. 5 R-Tree representation for full car assembly. |
3 Results and discussions
Most of the CAE tools supports programming interpreter to develop tools. ANSA Beta is one of the powerful and advance pre-processing tool used in automotive industry for finite element model preparation. ANSA Beta supports Python language to enhance their tool. R-tree algorithm is implemented using Python language in ANSA Beta. Martin et al. (1988) showed how objects can be put into boxes [8]. As discussed in methodology section R- Tree is implemented using bounding boxes as shown in Figure 6.
Script is developed using Python interpreter and results are tested on various assembly. As shown in Figure 7 script is tested firstly on small crankshaft assembly. Input for search is given as piston part then nearest part crankshaft is highlighted correctly with this approach.
It was interesting to test the developed R-tree script on large assembly. As shown in Figure 8 when input for the large model is given as wheel rim, it has searched correctly the first neighbour part disc which is highlighted by red boundary. Now it is very easy to find exact near part or other features with this script which was time consuming task with the conventional process.
It is very useful in model connections to identify nearest part to facilitate the connections. Figure 9 shows finite element model input of seat assembly. Side frames require bolted connections between them. To automate this connections with the script, it is essential to identify nearest frame for the given input frame, so that connections between them can be automated. When input is given as one side frame the other nearest frame is highlighted automatically as shown in Figure 9.
As stated earlier the main requirement was to handle large assembly models with an efficient search. Time study is performed by plotting the graph between number of parts and time to search near part. Figure 2 indicates that as number of parts increases, time taken to search neighbour part is increasing exponentially. It indicates that conventional search approach is not suitable for large assembly. For large models it does not work.
Developed neighbour search script was run on different models with increasing number of parts to measure the time. Figure 10 shows time study with newly implemented R-tree approach.
Figure 10 indicates that as number of parts increases, time taken to search neighbour part is also increases initially and then become almost constant. For large models the searching time is almost constant after some threshold. This indicates, it is capable of handling large assembly.
The comparison between Figures 2 and 10 shows, conventional search approach is less effective than implemented R-tree search algorithm. The new approach has implemented and tested for mentioned problems successfully.
 |
Fig. 6 R-Tree implementation for full car assembly. |
 |
Fig. 7 Script output with R-Tree approach to identify nearest part. |
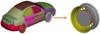 |
Fig. 8 Script output with R-Tree approach for full car assembly. |
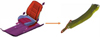 |
Fig. 9 Script output with R-Tree approach for to facilitate model connections. |
 |
Fig. 10 Time-study with newly implemented R-tree approach. |
4 Conclusion
R-Tree data structure is implemented in one of the CAE tool successfully. Implementation of R-tree has tested from small model assembly to large complex assembly. Comparison of plotted graphs indicates, implemented process is efficient. Developed neighbour search script can be implemented not only in automatic connections and mid surface generation but also other algorithms which require nearest neighbour search. R-tree can be implemented in other CAD and CAE tools to boost the searching process with better results.
Acknowledgments
The authors would like to thank RNTBCI for having given opportunity for the post graduate student of VIT Chennai, India Mr. Vaibhav to do internship at their facility.
References
- D.-P. Sheen, T.-G. Son, Dimension Reduction of Solid Models by Mid-Surface Generation, 2008 [Google Scholar]
- A. Guttman, R-trees: a dynamic index structure for spatial searching, in: Proceedings ACM SIGMOD Conference, Boston, MA, 1984, pp. 47–57 [CrossRef] [Google Scholar]
- N. Roussopoulos, S. Kelley, F. Vincent. Nearest neighbor queries, in: Proceedings ACM SIGMOD Conference, San Jose, CA, 1995, pp. 71–79 [CrossRef] [Google Scholar]
- Y. Manolopoulos, R-trees have grown everywhere, 2013 [Google Scholar]
- H.K. Ahn, N. Mamoulis, H.M. Wong, A Survey on multidimensional access methods, 2013 [Google Scholar]
- Q. Zhu, J. Gong, Y. Zang, An efficient 3D R-tree spatial index method for virtual geographic environments, 2007 [Google Scholar]
- P. Patel, Comparison of advance tree data structures, 2013 [Google Scholar]
- R.R. Martin, P.C. Stephenson, Putting objects into boxes, 1988 [Google Scholar]
Cite this article as: Vaibhav Shelar, Selamani Subramani, Jebaseelan Davidson, R-tree data structure implementation for Computer Aided Engineering (CAE) tools, Int. J. Simul. Multidisci. Des. Optim. 12, 6 (2021)
All Figures
 |
Fig. 1 Neighbour search requirement for mid-surface extraction. |
| In the text | |
 |
Fig. 2 Time study for conventional approach. |
| In the text | |
 |
Fig. 3 Neighbour search requirement for connections. |
| In the text | |
 |
Fig. 4 R-tree algorithm. |
| In the text | |
 |
Fig. 5 R-Tree representation for full car assembly. |
| In the text | |
 |
Fig. 6 R-Tree implementation for full car assembly. |
| In the text | |
 |
Fig. 7 Script output with R-Tree approach to identify nearest part. |
| In the text | |
 |
Fig. 8 Script output with R-Tree approach for full car assembly. |
| In the text | |
 |
Fig. 9 Script output with R-Tree approach for to facilitate model connections. |
| In the text | |
 |
Fig. 10 Time-study with newly implemented R-tree approach. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




