EDP Sciences logo
Submit your paper
Search
Menu
Home All issues Volume 14 (2023) Int. J. Simul. Multidisci. Des. Optim., 14 (2023) 15 Full HTML
Open Access
Issue
Int. J. Simul. Multidisci. Des. Optim.
Volume 14, 2023
Article Number 15
Number of page(s) 8
DOI https://doi.org/10.1051/smdo/2023013
Published online 04 December 2023

© Z. Zou et al., Published by EDP Sciences, 2023

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

As a 21st century green engineering metal structure material, magnesium alloy is characterized by low density, high specific strength and stiffness, good damping performance, convenient machining and easy recycling [1–4]. These advantages make it widely used in automotive, 3C aerospace and other fields [5–7]. However, magnesium and magnesium alloys are HCP structure [8], when the deformation temperature is below 225 °C, plastic deformation is limited to the basal plane {0001}<11 2 0> slip and pyramidal plane {10 1 2}<10 1 1> twinning [9–12]. Figure 1 gives HCP structure of magnesium alloys. Its plasticity at room temperature is very low, which severely limits the magnesium and magnesium alloy applications [13].

To realize the value of magnesium and magnesium alloys, we must firstly solve the plastic problem. From the Hall-Petch formula (1) it can be known that grain refinement can improve the strength and ductility of the material: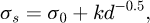(1)

where σs is yield strength, σ0 is the yield limit of monocrystal, k is a constant and d is the grain size. Under normal circumstances, the material slip system number determines the value of Taylor coefficient. There is a positive relationship between the value of k and Taylor coefficients. magnesium and magnesium alloys Taylor coefficient are larger due to the hcp structure relative to the face-centered cubic and body centered cubic, so its k is larger, and the potential through grain refinement method to improve the magnesium alloy plastic of is much greater than the iron alloy, aluminum alloy, etc. [14–16]. The main reason why finer-grained materials are stronger and harder than coarser-grained materials are that fine materials have a relatively large grain boundary area [17,18].

Equal channel angular processing is developed by Segal and is one of the most effective methods to improve one of the plastics materials currently [19–21]. Many studies have proved the equal channel angular extrusion can significantly refine the material grain. Aiming at the research on the deformation mechanism of equal channel angular extrusion, Xu et al. [22] studied the deformation uniformity of multi-pass ECAE process by using finite element analysis. He et al. [23]. found that isometric angle extrusion was performed on Fe-0.8C all-pearlitic steel at 923 K. After one isometric angle extrusion, the carburized lamellae were bent, kinked and fractured, and their spacing was significantly reduced. After four passes, the grain size was submicron ultra-fine biphasic (ferrite + carburite) and transformed the planar lamellae into equiaxed three-dimensional grains. Dynamic and continuous recrystallization occurs during the isometric angular extrusion deformation, forming isometric ferrite grains with an average size of 400 nm. Jiang and Da [24] extruded two kinds of Al-Mg-Mn alloy having similar composition but with and without Zr addition at 350 °C and the crystal grains of 1-2 µm were obtained after six times. Figure 2 shows schematic diagram of an ECAP die. Two channels of equal cross-sectional area intersected at a certain angle. One angle is died angle Φ, another is dying corner angle Ψ. In Equal channel angular pressing process, the billet moves downward the punch pressure P. when it is through the die corner, the billet will produce the nearly ideal shear deformation. Since the deformation process does not change the cross-sectional shape and area of the material, so the total strain can be accumulated from repeated extrusion. Under ideal conditions, the size of the shear strain after one pass by the formula (2) [25–28] determined by: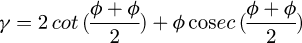(2)

In addition, the total equivalent strain after N passes can be represented by the formula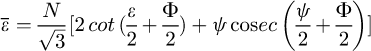 (3):(3)

Only if one assumption is met which is no friction, the formula (3) is only established [29,30]. Some researchers [31,32] have been verified the formula (3) through experimental study and have proved its rationality. Through finite element simulation, it is found that the dead zone is easily generated when Φ = 90° and Ψ = 0°, while it can be minimized when Φ = 90° and Ψ = 20° [33–35].

When Ψ = 0, Φ = 2 ϕ, the above formula can be described as: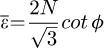(4)

This formula is consistent with the equivalent strain accumulation formula derived by Segal earlier using the slip line method [36].

In this paper, dynamic simulation of AZ31 magnesium alloy equal channel angular processing was carried out through finite element software Deform-2D, which simulated the deformation under different process parameters and analyzed the changes of field quantities during the deformation of magnesium alloy AZ31 ECAP.

thumbnail Fig. 1

HCP structure of magnesium alloy.
thumbnail Fig. 2

Schematic diagram of an ECAP die.

2 Finite element model

The finite element software Deform-2D software is a set of process simulation system based on finite element for the analysis of metal forming and related industry forming process and heat treatment processes. During the simulation, the billet is magnesium alloy square billet AZ31 of size 12 × 12 × 60 mm. Deform software material library has no the specific parameters of AZ31 magnesium alloy, so it is needed to determine the flow stress of AZ31 magnesium alloy relations, that is equation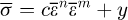 (5):(5)

Where c and y are constants, c = 205, y = 0. The strain index n = 0.044, the strain rate exponent m = 0.144. During equal channel angular processing, the geometry of the mold doesn't change, so the die is set to a rigid body during the simulation process, the billet is a deformable body, so it is set as a rigid plastic body. The meshing number is 8000, and the node number is 8241. The die parameters include die channel angle Φ and die corner angle Ψ. Theoretically, die channel angle Φ and die corner angle Ψ are in the range of 0° to 180°, but the actual die corner angle Ψ is preferably in the range of from 0° to 90°, the die channel angle Φ is preferably in the range of 90° to 150°. The specific parameters are shown in Table 1. During the finite element simulation, the size of the die corner angle is mainly determined by the radius of the outer arc of the die. Figure 3 gives the relationship between the die corner angle, the die outer arc radius and the width of the die channel. From Figure 3, the relationship between die corner angle, the die outer arc radius and width of the die channel can be deduced [37,38]: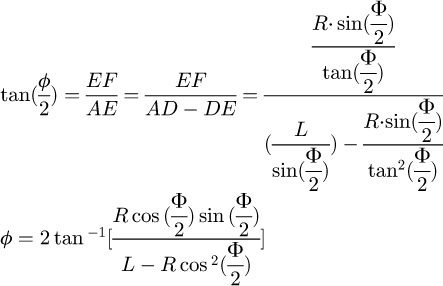(6)

When die channel angle Φ = 90°,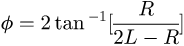(7)

When die channel angle was 90° and the value of the die corner angle were 15°, 26°, 37° and 52° respectively, the corresponding radius R can be calculated by bringing them into equation (7), and they are 2.79 mm, 4.5 mm, 6 mm, and 7.87 mm, respectively.

In order to analyze the uniformity of the deformation of the workpiece. Figure 4 gives three sections and nodes where the deformation was observed: the upper surface, the middle surface and the lower surface. Thirteen nodes were selected for each section. The field quantities of these sections and nodes were analyzed.

Table 1

The process parameters for the simulations of the square-section channel of ECAP process.

thumbnail Fig. 3

The relationship between the die corner angle, the die outer arc radius and of the width of the die.
thumbnail Fig. 4

Sections and nodes selected to observe deformation.

3 Results and analysis

3.1 Effect of die channel angle

Table 1 shows each parameter value, the selected value of die channel angles is 90°, 100°, 110° and 120°.The die corner angle is 37° and the inner arc radius r is 2 mm in the same time. Figure 5 shows the effective strain of nodes on three sections of workpiece: (a) Φ = 90°; (b) Φ = 100°; (c) Φ = 110°; (d) Φ = 120°. The horizontal axis of the curve represents distance of each node from the workpiece left side surface and the vertical axis represents the equivalent strain of each node. As can be seen from the figure the workpiece after deformed can be divided into three parts, namely the head deformation zone, the main deformation zone and tail deformation zone, which is consistent with the study of Xu et al. [39]. The head deformation zone: This is the first extrusion part, which is 50–60 mm part in the figure. The deformation of this part is very uneven, equivalent strain distribution gradient is bigger. The main deformation zone: This section takes up about 2/3 of workpiece along the length direction, which is 10–50 mm part. In the horizontal direction, the equivalent strain distribution is uniform. But in the direction of perpendicular to the horizontal direction of workpiece, the deformation is not uniform. The tail deformation zone: that is in the deformation stage, which is in the part of the 0–10 mm. This part deformation is not complete. if realized extrusion continuously of the workpiece, there is no tail deformation, and therefore this part can be negligible. From the figure, it can also be seen that with the increase of the die channel angle, the upper, equivalent strain gap of middle and lower three section gets smaller, that is, the greater the die channel angle, the more uniform deformation of the workpiece.

thumbnail Fig. 5

Effective strain of nodes on three sections of workpiece: (a) Φ = 90°; (b) Φ = 100°; (c) Φ = 110°; (d) Φ = 120°.

3.2 Effect of die corner angle

Figure 6 represents the equivalent strain curves at different nodes of the three cross-sections when the die corner angle are 15°, 26°, 37° and 52°, respectively, and the die channel angle is 90°. From the figure, it can be seen that the die corner angle has little effect on the size of the equivalent strain of the workpiece, and has no significant effect on the deformation geometry and deformation uniformity of the workpiece. But this does not mean that die corner angle does not affect the magnesium alloy ECAP deformation. Figure 7 presents the deformation of the workpiece and the mesh during simulation when the die corner angle are respectively 15°, 26°, 37° and 52° whit the die channel angle of 90°. The four selected die corner angle could not prevent the formation of the dead zone. The dead zone is the gap formed between the workpiece and the die as the workpiece passes through the die corners. The area of the dead zone increases as the angle of the die corner angle increases. Therefore, it is necessary to select smaller die corner angles in order to produce smaller dead zones in the ECAP process. The element of the unsqueezed workpiece is rectangular, and the rectangular element deforms into an elongated shape, as shown at nodes p4, p5, and p6, which are subjected to shear when the workpiece passes through the die corner. When the mold corner angle is different, the tail of the workpiece will appear different degrees of warping phenomenon, that is, p1, p2, p3 can not maintain the level. The larger the die angle, the larger the angle between p1, p2, p3 and the horizontal direction, and the more serious the warpage of the workpiece. When the die channel angles are 37° and 52°, a small gap is also formed between the die and the upper and lower surfaces of the workpiece, which may result in a slight reduction in the longitudinal dimension of the extruded workpiece.

The deformation characteristics of the ECAP process were analyzed and an algorithm for rigid-plastic finite elements was given. The mechanism of the ECAP process for square and round workpieces were analyzed using the commercial metal forming finite element code DEFORM-2D. From the results of the study, the die geometry of ECAP has a large influence on the extrusion process. The strain distribution on the ECAP with different die channel angles is the same, and the derived equation (3) agrees well with the actual simulation results. A range of optimum values for the die channel angle and die corner angle is given, taking into account the effect of deformation intensity and stress on the die. For materials with low resistance to deformation, it is necessary to obtain workpieces with good deformation distribution and high equivalent strain values. When the strength of the die is sufficient, smaller die channel angle and die corner angle can be selected to improve the cumulative deformation effect. When the deformation resistance of the material is high, it is recommended to select larger die channel angles and mold corners. Therefore, the die channel angle and die corner angle of ECAP should be carefully considered in the experiment.

thumbnail Fig. 6

Effective strain of nodes on three sections of workpiece: (a) Ψ = 15°; (b) Ψ = 26°; (c) Ψ = 37°; (d) Ψ = 52°.
thumbnail Fig. 7

The deformation in the cross-section of workpiece for different corner angle at Φ = 90°: (a) corner angle of Ψ = 15°; (b) corner angle of Ψ = 26°; (c) corner angle of Ψ = 37°; (d) corner angle of Ψ = 52°.

4 Conclusions

The effects of the die channel angle and the die corner angle on workpiece deformation uniformity have been researched and analyzed by the two-dimensional finite element simulation of magnesium alloy ECAP process, and the following conclusions are drawn:

  • According to the deformation after extrusion, the workpiece can be divided into three parts: head deformation zone, main deformation zone and tail deformation zone. In the main deformation zone, the die channel angle has little effect on the uniformity of the longitudinal deformation of the workpiece, and the larger the die channel angle is, the more uniform the longitudinal deformation of the workpieces are.

  • The die corner angle has little effect on the uniformity of longitudinal deformation of the workpiece, and when the die corner angles are different, the equivalent deformation in the horizontal direction does not change much.

  • The die corner angles have some influence on the dead zone area and workpiece warpage. The dead zone area and workpiece warpage increase with the increase of die angle. When the mold angle is 37° and 52°, a small gap is formed between the mold and the upper and lower surfaces of the workpiece.

Funding

The study was supported by Key industrial projects to replace old and new driving forces in Shandong Province, China (New Energy Industry 2021-03-3), Natural Science Foundation of Shandong Province, China (ZR2021ME182), National College Student Innovation and Entrepreneurship Program (S20211043001, 202210430010 and 202210430008), the Science and Technology Enterprise Innovation Program of Shandong Province, China (2022TSGC2108, 2022TSGC2402, 2023TSGC085, 2023TSGC0119, 2023TSGC0759 and 2023TSGC0961), the Shandong Graduate Education and Teaching Reform Research Project (Grant No. SDYJG21169) and the High quality curriculum construction project of Shandong Jianzhu University graduate education (YZKC202210 and ALK202210).

Conflicts of interest

The authors declare no conflict of interest.

Author contributions

Conceptualization, G.Z.; Methodology, S.X., G.Z. and X.S.; Software, X.X. and T.L.; Formal analysis, S.X.; Data curation, S.X. and X.X.; Writing − original draft, G.R.; Writing − review & editing, X.X.; Funding acquisition, S.X. All authors have read and agreed to the published version of the manuscript.

References

  1. W. Wu, L. Wang, G. Huang, H. Zhang, W. Cheng, H. Wang, K.S. Shin, Effect of multi-pass continuous screw twist extrusion process on microstructure evolution, texture, and mechanical properties of AZ31 magnesium alloy, Mater. Today Commun. 34, 105508 (2023) [CrossRef] [Google Scholar]
  2. A. Asgari, H. Delavar, M. Sedighi, Microstructure and surface integrity of machined AZ91 magnesium alloy, J. Mater. Res. Technol. 22, 735–746 (2023) [CrossRef] [Google Scholar]
  3. L. Govind Sanjeev Kumar, D. Thirumalaikumarasamy, K. Karthikeyan, M. Mathanbabu, M. Ashokkumar, C.S. Ramachandran, An overview of recent trends and challenges of post treatments on magnesium alloys, Mater. Today: Proc. 78, 700–707 (2023) [CrossRef] [Google Scholar]
  4. J. Song, J. Chen, X. Xiong, X. Peng, D. Chen, F. Pan, Research advances of magnesium and magnesium alloys worldwide in 2021, J. Magnes. Alloys 10, 863–898 (2022) [CrossRef] [Google Scholar]
  5. M. Ebrahimi, Q. Wang, S. Attarilar, A comprehensive review of magnesium-based alloys and composites processed by cyclic extrusion compression and the related techniques, Prog. Mater. Sci. 131, 101016 (2023) [CrossRef] [Google Scholar]
  6. J. Kubásek, P. Minárik, K. Hosová, S. Šašek, M. Knapek, J. Veselý, J. Stráská, D. Dvorský, M. Čavojský, D. Vojtěch, Novel magnesium alloy containing Y, Gd and Ca with enhanced ignition temperature and mechanical properties for aviation applications, J. Alloys Compd. 877, 160089 (2021) [CrossRef] [Google Scholar]
  7. G.G. Wang, J.P. Weiler, Recent developments in high-pressure die-cast magnesium alloys for automotive and future applications, J. Magnes. Alloys 11, 78–87 (2022) [Google Scholar]
  8. C. Xue, S. Li, Z. Chu, Q. Yang, Y. Li, L. Ma, L. Tuo, Molecular dynamics study on the effect of temperature on HCP→FCC phase transition of magnesium alloy, J. Magnes. Alloys (2022) doi:10.1016/j.jma.2022.03.013 [Google Scholar]
  9. D. Arola, C.L. Williams CL, Estimating the fatigue stress concentration factor of machined surfaces, Int. J. Fatigue 24, 923–930 (2002) [CrossRef] [Google Scholar]
  10. M. Hareendran, S. Sreejith, A study on surface quality of thin-walled machined parts, Mater. Today: Proc. 5, 18730–18738 (2018) [CrossRef] [Google Scholar]
  11. D. Mingxia, G. Chunhuan, S. Qianfei, J. Fengchun, L. Liyu, L. Jifeng, X. De, L. Chuanming, S. Haolun, Improving mechanical properties of austenitic stainless steel by the grain refinement in wire and arc additive manufacturing assisted with ultrasonic impact treatment, Mater. Sci. Eng. A 857, 144044 (2022) [CrossRef] [Google Scholar]
  12. A. Rodriguez, L.N.L. de Lacalle, O. Pereira, A. Fernandez, I. Ayesta, Isotropic finishing of austempered iron casting cylindrical parts by roller burnishing, Int. J. Adv. Manuf. Technol. 110, 753–761 (2020) [CrossRef] [Google Scholar]
  13. S. Prithivirajan, G.M. Naik, S. Narendranath, V. Desai, Recent progress in equal channel angular pressing of magnesium alloys starting from Segal's idea to advancements till date − A review, Int. J. Lightweight Mater. Manuf. 6, 82–107 (2023) [Google Scholar]
  14. P. Snopiński, Exploring microstructure refinement and deformation mechanisms in severely deformed LPBF AlSi10Mg alloy, J. Alloys Compd. 941, 168984 (2023) [CrossRef] [Google Scholar]
  15. Y.-j. Chen, Q.-d. Wang, J.-b. Lin, M.-p. Liu, J. Hjelen, H.J. Roven, Grain refinement of magnesium alloys processed by severe plastic deformation, Trans. Nonferrous Met. Soc. China 24, 3747–3754 (2014) [CrossRef] [Google Scholar]
  16. G. Vignesh, D. Barik, S. Aravind, P. Ragupathi, M. Arun, Numerical investigation of dimple-texturing on the turning performance of hardened AISI H-13 steel, Int. J. Simul. Multidiscip. Des. Optim. 13, 639–651 (2021) [Google Scholar]
  17. R. Naseri, M. Kadkhodayan, M. Shariati, Static mechanical properties and ductility of biomedical ultrafine-grained commercially pure titanium produced by ECAP process, Trans. Nonferrous Met. Soc. China 27, 1964–1975 (2017) [CrossRef] [Google Scholar]
  18. Z. Yang, A. Ma, H. Liu, D. Song, Y. Wu, Y. Yuan, J. Jiang, J. Sun, Managing strength and ductility in AZ91 magnesium alloy through ECAP combined with prior and post aging treatment, Mater. Charact. 152, 213–222 (2019) [CrossRef] [Google Scholar]
  19. A. Awasthi, A. Gupta, K.K. Saxena, R.K. Diwedi, Equal channel angular processing on aluminium and its alloys − A review, Mater. Today: Proc. 56, 2388–2391 (2022) [CrossRef] [Google Scholar]
  20. M.M. Hoseini-Athar, R. Mahmudi, R.P. Babu, P. Hedström, Microstructure and superplasticity of Mg-2Gd-xZn alloys processed by equal channel angular pressing, Mater. Sci. Eng. : A 808, 140921 (2021) [CrossRef] [Google Scholar]
  21. X. Zhang, Y. Cheng, Tensile anisotropy of AZ91 magnesium alloy by equal channel angular processing, J. Alloys Compd. 622, 1105–1109 (2015) [CrossRef] [Google Scholar]
  22. S. Xu, G. Zhao, X. Ma, G. Ren, Nite element analysis and optimization of equal channel angular pressing for producing ultra-fine grained materials, J. Mater. Process. Technol. 184, 209–216 (2007) [CrossRef] [Google Scholar]
  23. T. He, Y. Xiong, F. Ren, Z. Guo, A.A. Volinsky, Microstructure of ultra-fine-grained high carbon steel prepared by equal channel angular pressing, Mater. Sci. Eng.: A 535, 306–310 (2012) [CrossRef] [Google Scholar]
  24. J.L. Ning, D.M. Jiang, Influence of Zr addition on the microstructure evolution and thermal stability of Al-Mg-Mn alloy processed by ECAP at elevated temperature, Mater. Sci. Eng. A: Struct. Mater. Prop. Microstruct. Process. 452, 552–557 (2007) [CrossRef] [Google Scholar]
  25. P. Frint, M.F.X. Wagner, Strain partitioning by recurrent shear localization during equal-channel angular pressing of an AA6060 aluminum alloy, Acta Mater. 176, 306–317 (2019) [CrossRef] [Google Scholar]
  26. I. Balasundar, M. Sudhakara Rao, T. Raghu, Equal channel angular pressing die to extrude a variety of materials, Mater. Des. 30, 1050–1059 (2009) [CrossRef] [Google Scholar]
  27. F. Djavanroodi, M. Ebrahimi, Effect of die channel angle, friction and back pressure in the equal channel angular pressing using 3D finite element simulation, Mater. Sci. Eng.: A 527, 1230–1235 (2010) [CrossRef] [Google Scholar]
  28. B.V. Patil, U. Chakkingal, T.S. Prasanna Kumar, Effect of geometric parameters on strain, strain inhomogeneity and peak pressure in equal channel angular pressing − a study based on 3D finite element analysis, J. Manuf. Process. 17, 88–97 (2015) [CrossRef] [Google Scholar]
  29. K.M. Agarwal, R.K. Tyagi, A. Kapoor, Deformation and strain analysis for grain refinement of materials processed through equal channel angular pressing, Mater. Today: Proc. 21, 1513–1519 (2020) [CrossRef] [Google Scholar]
  30. K. Mohan Agarwal, R.K. Tyagi, A. Dixit, Theoretical analysis of equal channel angular pressing method for grain refinement of metals and alloys, Mater. Today: Proc. 25, 668–673 (2020) [CrossRef] [Google Scholar]
  31. N. Fakhar, M. Sabbaghian, Hot shear deformation constitutive analysis of fine-grained ZK60 Mg alloy sheet fabricated via dual equal channel lateral extrusion and sheet extrusion, Trans. Nonferrous Met. Soc. China 32, 2541–2556 (2022) [CrossRef] [Google Scholar]
  32. X. Sun, D.-Y. Wu, M. Kang, K.T. Ramesh, L.J. Kecskes, Properties and hardening behavior of equal channel angular extrusion processed Mg-Al binary alloys, Mater. Charact. 195, 112514 (2023) [CrossRef] [Google Scholar]
  33. A. Ghosh, M. Ghosh, 3D FEM simulation of Al-Zn-Mg-Cu alloy during multi-pass ECAP with varying processing routes, Mater. Today Commun. 26, 102112 (2021) [CrossRef] [Google Scholar]
  34. M.I. Abd El Aal, 3D FEM simulations and experimental validation of plastic deformation of pure aluminum deformed by ECAP and combination of ECAP and direct extrusion, Trans. Nonferrous Met. Soc. China 27, 1338–1352 (2017) [CrossRef] [Google Scholar]
  35. A.I. Alateyah, M.M.Z. Ahmed, M.O. Alawad, S. Elkatatny, Y. Zedan, A. Nassef, W.H. El-Garaihy, Effect of ECAP die angle on the strain homogeneity, microstructural evolution, crystallographic texture and mechanical properties of pure magnesium: numerical simulation and experimental approach, J. Mater. Res. Technol. 17, 1491–1511 (2022) [CrossRef] [Google Scholar]
  36. Y. Iwahashi, J. Wang, Z. Horita, M. Furukawa, T. Langdon, Principle of equal channel angular pressing for the processing of ultra-fine grained materials[J], Scripta Mater. 35, 143–146 (1996) [CrossRef] [Google Scholar]
  37. M. Sabbaghian, R. Mahmudi, K.S. Shin, A comparative study on the microstructural features and mechanical properties of an Mg-Zn alloy processed by ECAP and SSE, Mater. Sci. Eng.: A 845, 143218 (2022) [CrossRef] [Google Scholar]
  38. T.A. Yilmaz, Y. Totik, G.M. Lule Senoz, B. Bostan, Microstructure evolution and wear properties of ECAP-treated Al-Zn-Mg alloy: effect of route, temperature and number of passes, Mater. Today Commun. 33, 104628 (2022) [CrossRef] [Google Scholar]
  39. S. Xu, G. Zhao, Y. Luan, Y. Guan, Numerical studies on processing routes and deformation mechanism of multi-pass equal channel angular pressing processes, J. Mater. Process. Technol. 176, 251–259 (2006) [CrossRef] [Google Scholar]

Cite this article as: Zhongping Zou, Ruilan Gao, Shubo Xu, Xianmeng Xue, Tingting Li, Guocheng Ren, Deformation mechanism finite element analysis and die geometry optimization of magnesium alloys by equal channel angular processing, Int. J. Simul. Multidisci. Des. Optim. 14, 15 (2023)

All Tables

Table 1

The process parameters for the simulations of the square-section channel of ECAP process.

In the text

All Figures

thumbnail Fig. 1

HCP structure of magnesium alloy.
In the text
thumbnail Fig. 2

Schematic diagram of an ECAP die.
In the text
thumbnail Fig. 3

The relationship between the die corner angle, the die outer arc radius and of the width of the die.
In the text
thumbnail Fig. 4

Sections and nodes selected to observe deformation.
In the text
thumbnail Fig. 5

Effective strain of nodes on three sections of workpiece: (a) Φ = 90°; (b) Φ = 100°; (c) Φ = 110°; (d) Φ = 120°.
In the text
thumbnail Fig. 6

Effective strain of nodes on three sections of workpiece: (a) Ψ = 15°; (b) Ψ = 26°; (c) Ψ = 37°; (d) Ψ = 52°.
In the text
thumbnail Fig. 7

The deformation in the cross-section of workpiece for different corner angle at Φ = 90°: (a) corner angle of Ψ = 15°; (b) corner angle of Ψ = 26°; (c) corner angle of Ψ = 37°; (d) corner angle of Ψ = 52°.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.