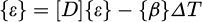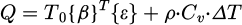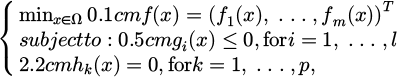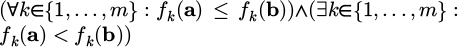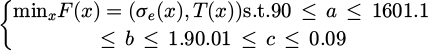| Issue |
Int. J. Simul. Multidisci. Des. Optim.
Volume 14, 2023
|
|
|---|---|---|
| Article Number | 16 | |
| Number of page(s) | 9 | |
| DOI | https://doi.org/10.1051/smdo/2023007 | |
| Published online | 04 December 2023 | |
Research article
Multi-objective optimization of the high electron mobility transistor
1
Centre de Recherche, IRDL CNRS UMR 6027, Université de Bretagne Sud, Lorient, France
2
Laboratory of Computer and Mathematical Process Engineering, ENSA Khouribga, Sultan Moulay Slimane University, Morocco
3
Hassan First University of Settat, FST, LIMII, BP: 577, Route de Casa, Settat, Morocco
4
Normandie University, INSA Rouen, LMN, 76000 Rouen, France
* email: amarabdelhamid20@gmail.com
Received:
6
March
2023
Accepted:
6
July
2023
In this paper, we present a new approach to improve the thermo-mechanical performance of the HEMT (high electron mobility transistor) technology. This study aims to solve two optimization problems. The first one is the optimization of the thermal behavior of the HEMT, through the optimization of its maximum operating temperature which influences the electrical characteristics such as electron mobility, and also influences the mechanical behavior of its structure. While the second problem will be the optimization of the mechanical behavior of the same technology, through the optimization of the stresses distribution that also influence the electrical characteristics and reliability of the HEMT structure. The resolution of these two optimization problems will be done, by the multi-objective optimization approach thanks to numerical tools such as Comsol multiphysics and Matlab software, which allows to solve these two problems simultaneously by taking into consideration the imposed constraints. The results obtained have optimized the thermo-mechanical behavior of the HEMT, which proves the efficiency of this approach to solve complex optimization problems.
Key words: HEMT / FEM / electro-thermo-mechanical / optimization / multi-objective
© A. Amar et al., Published by EDP Sciences, 2023
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The HEMT technology based on GaN (gallium nitride) has been used extensively in mechatronic systems and high-power systems. Thanks to its special structure and electro-thermal characteristics compared to other transistors, the HEMT technology can operate in the exceptional conditions like high temperature, high frequency and high power [1,2]. All these many advantages make the HEMT the best element to use in different fields such as airborne systems, electrical vehicles, satellites, and telecommunications [3,4].
During the operation of the HEMT, it dissipates power in the active zone (the output of the gate next to the drain), this phenomenon causes a rise in temperature within the HEMT due to the self-heating of the component. Whereas majorities of its characteristics, like thermal conductivity and electrons mobility, are a function of temperature, they can be influenced or deteriorated with the temperature rising in the structure [5–7]. That can also generate mechanical degradation in the HEMT structure, and some physical characteristics of the materials are related to the temperature and strain simultaneously. These degradations can have different forms: stresses, displacements, or strains.
Therefore, a modeling and optimization study must be performed to analyze the thermomechanical behavior of the HEMT and improve its performance. In this context, several authors have developed the electrical, thermal, or electrothermal model using the finite element method in order to analyze the electrical and thermal behavior of the HEMT and to study the influence of the operating conditions on the thermal and electrical performance of the component [8–11]. However, some works have dealt with complete modeling (electro-thermo-mechanical) or mechanics only in order to identify the interaction between thermal, electrical, and mechanical variables [2,12–14]. The modeling step allows observing and analyzing the structural failures. On the other hand, an optimization is an approach that aims to improve the performance of systems. It is based on the minimization of an objective function related to the optimization problem. In the literature, we can find several types of optimization. More than one objective function is treated by the multiobjective optimization problem (MOP) and it is not to consist of finding an optimal solution corresponding to each objective function but to find a set of solutions called Pareto-optimal front [15]. Using native MOP techniques is crucial for real-world applications because of the multiplicity of principles involved. The handling of participating variables appropriately is the key to successful optimization. When the objective function for an optimization problem is non-linear and non-differentiable, evolutionary algorithm (EA) techniques are typically used to find the global optimum.
In this paper, we will treat the HEMT technology using a new optimization method. We will develop a complete multiphysics model, which allows simulation of the electro-thermal and the thermo-mechanical behavior. Thanks to the modeling step, we can study the influence of the operating conditions on the HEMT structure behavior, and identify the different parameters that impact the performance of the component. In the next step, we will adjust the multi-objective optimization approach to the HEMT technology. We will couple the finite element model (FEM) using Comsol multiphysics software, to the multi-objective optimization model using Matlab software, which allows us to optimize the HEMT multiphysics behavior by the determination of the optimal variables.
To achieve this objective, our paper will be composed of several parts. For the first time, we will start by describing the HEMT and its applications. In the next, we will detail the multiphysics model of this technology. Then we will present the optimization approach used in this study case. In the last section, the results obtained by the multiobjective method applied to the HEMT will be presented and discussed.
2 Device description
The structure of the HEMT technology is very special, it is composed of different layers of different materials (Fig. 1). The basis of the component construction is represented by the silicon carbide (SiC) layer [2,16,31]. The layer that ensures the tuning of the mesh of the GaN layer and the substrate is called the nucleation layer. One of the most important layers is the GaN layer, which has two-dimensional gas (2DEG) above. Another important layer is the AlGaN layer which creates a heterojunction with the previous layer (GaN). In addition, the HEMT has other layers that provide other functions. To control voltage and current, it has three electrodes, the drain, and source with an ohmic contact and the gate with a Schottky contact [2,17,18]. For our case study, we are interested in the single-finger HEMT. The geometrical dimensions are thAlGaN = 0.03 μm, thGaN = 1.3 μm and thSiC = 100 μm represent the thickness of the AlGaN, GaN layers, and the substrate. And the width of the gate is WGate = 100μm [2].
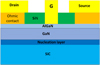 |
Fig. 1 Structure of the HEMT technology. |
3 Multi-physics modeling of HEMT
In this section, we will present a multiphysics modeling of the HEMT technology using the finite element method (FEM). That will be in two parts: firstly, electrothermal modeling and secondly thermo-mechanical modeling. Then, we will present the results of the numerical simulations at the end of this section.
3.1 Electro-thermal modeling
The HEMT technology dissipates power at the active area in the gate output during its operation [19,30]. The dissipated power is related to the current and voltage applied between the component terminals, such as [11]:
where Vds and Ids are respectively the voltage and the current drain-source. We will deal with the heat transfer at the component structure, for studying its electro-thermal behavior. This transfer is globally done by conduction mode, other modes (radiation and convection) are negligible in that they represent just less than 1.5% of the global transfer [2,20,21]. Based on the principal heat exchange mode, the heat equation expression will be as follows [22]:
where:
T: temperature (K),
K: thermal conductivity (W/m/K),
Cp: thermal mass capacity (J/Kg/K),
ρ: density (kg/m3),
Q: dissipated heat (J).
The precedent equation links the dissipated heat with different thermal parameters. In addition, it allows describing the thermal behavior of the component structure, as a function of the operating conditions, especially the dissipated power. To develop the electrothermal model we need the thermal properties of the material of the layer, which we have classified in Table 1. For some material properties, the thermal conductivity is temperature dependent [3,23,24].
We have developed the finite element model using Comsol multiphysics software as a function of boundary conditions. The first condition is the linear dissipated power (Pdiss) in (W/mm) applied in the active area of the HEMT and the second is the reference temperature (Tref) in the substrate.
The results of the numerical simulations for the electrothermal model are presented in Figure 2, and we have compared them with the experimental results. The experimental method used is the Raman micro-spectrometry method [2,25]. In the same figure, we can observe the increase in operating temperature according to the linear dissipated power. The increase follows a non-linear evolution, which can be explained by the non-linearity of some material properties. In addition, it is also observed that the experimental and simulation curves are well correlated. However, the divergence of these curves especially in the cases of very high dissipated power is due to the negligence of the other two modes of thermal exchange, and the nonlinearity of the properties of materials as we have previously mentioned.
Materials thermal properties.
 |
Fig. 2 Evolution of the operating temperature as a function of the dissipated power. |
3.2 Thermo-mechanical modeling
The thermo-mechanical modeling allows studying the thermal behavior impact on the mechanical one of this technology. The temperature increase in the device because of the dissipated power can cause mechanical degradation in its structure. In order to identify this degradation, a thermo-mechanical model will be developed which allows us to link thermal parameters with mechanical ones. The temperature is a very important thermal parameter. The mechanical parameters can have several forms such as displacements, strains, and stresses. Coupling the thermal model with the mechanical one can be assured by the equations of thermo-elasticity. That, the entropy density and the strains vector can be related to other parameters and can be defined by the following expressions [2,22]:
where:
{ϵ} the vector of total strains,
{σ} stress vector,
{α} the vector of thermal expansion coefficients,
Δ T = T − Tref the temperature difference,
[D] the elastic stiffness matrix.
According to the equation (4), entropy is related to different thermal and mechanical parameters like temperature difference, stress, and others. From the thermodynamics law, the entropy density is a function of heat density and can be expressed as follows:
On the other hand, the thermoelastic coefficients vector {β} can be expressed as follows :
And Cv represent the specific heat at constant volume and can be expressed as follows:
The global equations are obtained by combining the precedent equations, and they will be expressed as follows [26]:
These equations allow linking the thermal parameters to the mechanical ones and ensure the thermomechanical coupling. The material's physical properties that we need to build the model are: the Yong modulus E, the Poisson's ratio ν, and the thermal expansion coefficient α. The values of these parameters are classified in the Table 2 [14,27]. We notice that some of the properties of the materials are already integrated into the Comsol material library [28].
Physical properties of materials.
Design variables.
HEMT optimal results.
3.3 Numerical simulation of stresses in the HEMT
The FEM was developed using Comsol software, With thermal and mechanical boundary conditions, the mechanical one has o forms of displacement applied in the SiC layer. This model allowed observing the von Mises stress distribution on the device structure. Based on Figure 3, This distribution is very high in the substrate layer that represents the growing base of the transistor, on both sides of the gate and in the AlGaN layer. These stresses exceed 4 GPa in these critical areas. Therefore, the functioning conditions of the HEMT technology have an important mechanical effect on the critical parts of its structure.
The same finite element model allows observing the stress evolution according to the different applied loads, we have carried out numerical simulations for the various values of the dissipated power, and we have fixed the value of the reference temperature. The numerical results are presented in Figure 4, we observe clearly that the stresses evolve according to the linear dissipated power, with a non-linear evolution. These stresses can reach important values, for the power of 12 W/mm, they can reach a value of 4.5 GPa.
 |
Fig. 3 Distribution of the von Mises stresses. |
4 Multi-objective optimization approach
More than one objective function is treated by the multiobjective optimization problem (MOP) and it is not to consist of finding an optimal solution corresponding to each objective function but to find a set of solutions called the Pareto-optimal front.
Let's consider the following multiobjective optimization problem (MOP):
where f is the vector of concurrent objective functions to optimise, m is the number of objective functions, x = (x1, … , xn) ∈ Ω is the D-dimensional decision space where each decision variable xi is bounded by lower and upper limits xli ≤ xi ≤ xui for i = 1, … , D, gi (x) are l inequality constraints and hk (x) are p equality constraints.
Let us first introduce some basic concepts of the multiobjective optimization [29]:
Pareto dominance: Let a = (a1, ..., an) and b = (b1, ..., bn) be two vectors. The vector a dominates the vector b if and only if a is partially less than b, i.e.:
(denotedbya ≻ b).
Pareto-optimal solution : A solution a ∈ Ω is said to be Pareto-optimal if there is no solution b ∈ Ω which dominates a, i.e.
Pareto-optimal set: The set PS of all Pareto-optimal solutions, as defined by:
Pareto front: The Pareto front, denoted PF, is the image of Pareto optimal set PS in the objective space and is defined as follows:
4.1 Multiobjective optimization based Backtracking Search Algorithm
Backtracking Search Algorithm (BSA) was initially developed for single-objective optimization problems only. In this paper, BSA was extended by making it suitable for handling MOPs. the main development concern the fitness values assigned to individuals in the population. This development with BSA's main strategies and algorithm simplicity allows the benefit from new capacities of exploration of the search space and of the use of an adapted search direction matrix, to obtain good efficiency and preserve the BSA's spirit.
Algorithm 1 gives the proposed pseudocode, where MaxG is the maximum number of generations. It is called BSAMO, integrating the fast non-dominated sorting and the crowding distance of Deb et al. [15], and BSA's mutation and crossover operators presented in [30].
Function P = BSAMO(D, N, m, f (x) , MaxG, xl, xu)
1: Generate the initial population P and the historical population Ph;
2: P : = Find_Non_Dominated_Crowding_Distance (P | f(x));
3: for t = 1 : MaxG, do
4: [Pc, Ph] : = BSA_Operator (P, xl, xu, Ph); // BSA_Operator:
Mutation and Crossover;
5: P : = Find_Non_Dominated_Crowding_Distance ([P;Pc] | f(x));
6: Sort and find the current Pareto optimal solution;
7: end for
In the elaboration of the fast non-dominated sorting procedure, the domination counts np, the number of solutions that dominate the solution p, and the set of solutions that the solution p dominates Sp are calculated for every solution. The first non-dominated front is thus created and initialized. Then, for each solution p with np = 0, each member q of its set Sp is visited, and its domination count is reduced by one. As a result, if for any member, the domination count is equal to zero, we put it in a separate list Q. The second non-dominated front is then created as the union of all individuals belonging to Q. The procedure is repeated for subsequent fronts (F3, F4, etc.) until all individuals are assigned their ranks. The fitness is set to a level number, lower numbers correspond to higher fitness (F1 is the best).
The crowding distance is the average distance between two individuals located on either side of the given particular solution along each objective, and estimating the diversity measure of individuals surrounding a given individual i in the population. Such distance is an estimation of the perimeter of the cuboid formed using the nearest neighbors. This metric represents half of the perimeter of the cuboid encompassing the solution i. The main consideration from the crowding distance is to find the Euclidean distance between each individual in a front based on their m objectives. The computation of the crowding distance, based on the normalized values of objectives, is given by Algorithm 2, where  and
and  are the maximum and minimum values of the mth objective function, respectively. The sum of individual crowding distance values corresponding to each objective gives the overall crowding distance value [30].
are the maximum and minimum values of the mth objective function, respectively. The sum of individual crowding distance values corresponding to each objective gives the overall crowding distance value [30].
1: n = |ℐ| // number of solutions in ℐ;
2: for each i, do
3: set ℐ[i]distance = 0;
4: end for
5: for each objective m, ℐ = sort (ℐ, m) do
6:ℐ[1]distance=ℐ[n]distance=∞
7: for i = 2 to (n − 1) do
8: ℐ[i]distance = ℐ[i]distance+(ℐ[i+1].m-ℐ[i-1].m)/(fmaxm-fminm);
9: end for
10: end for
In this algorithm, ℐ is a non-dominated set, n is the number of elements of ℐ, ℐ[i]m is the mth objective value of the ith individual in ℐ, and sort(ℐ, m) is sorting of the individuals of ℐ according to the mth objective. The theoretical aspect of this algorithm is developed in [30,31].
5 Numerical simulation
5.1 Optimization problem
The implementation of HEMT technology in mechatronic systems can be accompanied by thermal phenomena such as self-heating, or mechanical phenomena such as stresses, deformations or displacements in its structure. All these phenomena can provoke failures of different forms for the HEMT, they can also limit its performances as we have mentioned in the previous parts. Therefore, limiting and controlling the effects of these phenomena is a challenge for developers and researchers in the field of this technology [2]. Especially since these phenomena directly influence its reliability and efficiency. As a result, our optimization problem under deterministic constraints by the multi-objective optimization method is expressed as follows:
where a, b and c are the deterministic design variables, σe (x) and T (x) are respectively the von Mises constraints and the temperature at the structure and F (x) is the objective function to be minimized.
Our optimization process requires the development of a coupling between the finite element model using Comsol multiphysics software and the multi-objective optimization model coded in Matlab software. The flowchart in Figure 5 shows the multi-objective optimization coupling process. The optimization work was entirely automated via a main script written in MATLAB. The script starts the Multi-objective optimization process by generating an initial population using a uniform random distribution function. Then the main script submits multiple sets of decision variables and waits for each individual objective function's values before proceeding further. MATLAB calls Comsol software for changing the input parameters to compute the thermomechanical responses taken as objective values and returns back those values to the optimization process for executing the multi-objective algorithm and displaying the optimal results.
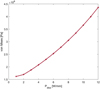 |
Fig. 4 Variation of the von Mises stresses. |
5.2 Results and discussion
In this section, we will present the results of the solution to our optimization problem. This problem is solved by the multi-objective optimization approach, and the objective function was the maximum operating temperature and the von Mises stresses. Concerning the deterministic constraints, we have chosen as deterministic variables three design parameters of the three layers that represent a great impact on the multiphysics behavior of the component. These parameters are the AlGaN, GaN, and SiC(Silicon Carbide) layers. In Table 3, we have classified the initial, maximum, and minimum values that we will use during the resolution of this optimization problem.
The multi-objective optimization in this part is carried out by using BSAMO and NSGA-II algorithms coupled with the FEM that we have developed by Comsol multiphysics software, according to the optimization process presented in Figure 5. The Pareto fronts obtained for both algorithms (BSAMO and NSGA-II), for population size and a maximum number of generations set respectively at 30 and 30, are shown in Figure 6 and the results from Table 3 and marked in bold present a comparison between the best objective functions optimal values found by the two algorithms for the airfoil.
The results from Figure 6 and Table 4 indicate that the expansibility of the Pareto fronts distribution by BSAMO is clearly better than NSGA-II when solving this optimization problem with good quality distribution and approximation. Also for the two multi-physics simulations, it obtains better optimal results for the objective functions.
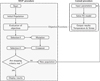 |
Fig. 5 Flowchart of the coupling process. |
 |
Fig. 6 Pareto solutions. |
6 Conclusion
In this paper, we have proposed an approach for improving the thermomechanical performance of the HEMT, using a multi-objective optimization method. The application of this approach is ensured due to the coupling of two models: firstly, the finite element model developed using Comsol multiphysics software, and the second one is the multi-objective optimization model using Matlab software, it is used to minimize two objective functions, the temperature and the von Mises stress with well-determined design variables. The application of this approach to the HEMT technology has allowed the exploration of new parameters of design satisfying a Pareto front that gives a good compromise of minimum values of temperature and von Mises stress. The multi-objective optimization method has shown its efficiency to solve optimization problems compared to the deterministic and classical methods.
References
- M.A. Alim, S. Afrin, A.A. Rezazadeh, C. Gaquiere, Thermal response and correlation between mobility and kink effect in GaN HEMTs, Microelectron Eng. 219, 111 (2020) [Google Scholar]
- A. Amar, B. Radi, H. El Abdelkhalak, Electrothermal reliability of the high electron mobility transistor (Hemt), Appl. Sci. 11, 10720 (2021) [CrossRef] [Google Scholar]
- A. Amar, B. Radi, A. El Hami, La modélisation thermique de transistor a haute puissance de type HEMT, Incertitudes Fiabilité Syst. Multiphys. 3, 1–7 (2019) [Google Scholar]
- A. Amar, B. Radi, A. El Hami, La modélisation thermique de transistor a haute puissance de type HEMT, Incertitudes Fiabilité Syst. Multiphys. 3 (2020) [Google Scholar]
- A. Amar, B. Radi, A. El Hami, Optimisation thermique du transistor à haute mobilité d'électron (HEMT) par la méthode CMA-ES 4 (2020) [Google Scholar]
- A. Amar, B. Radi, A. El Hami, Optimization based on electro-thermo-mechanical modeling of the high electron mobility transistor (HEMT), Int. J. Simul. Multidiscip. De. Optim. 13,2 (2022) [CrossRef] [EDP Sciences] [Google Scholar]
- A. Amar, B. Radi, A. El Hami, Reliability based design optimization applied to the high electron mobility transistor (HEMT), Microelectron. Reliabil. 124, 114299 (2021) [CrossRef] [Google Scholar]
- M.G. Ancona, S.C. Binari, D.J. Meyer, Fully coupled thermoelectromechanical analysis of GaN high electron mobility transistor degradation, J. Appl. Phys. 111, 0–16 (2012) [CrossRef] [Google Scholar]
- R. Aubry, Etude des aspects électrothermiques de la fikière HEMT AlGaN/GaN pour application de puissance hyperfréquence, PhD thesis, L'université des sciences et technologiques de Lille, 2004 [Google Scholar]
- L. Baczkowski, J.C. Jacquet, O. Jardel, Temperature measurements in RF operating conditions of AlGaN/GaN HEMTs using IR microscopy and Raman spectroscopy, Eur. Microwave Week 5, 152–155 (2015) [Google Scholar]
- K.R. Bagnall, E.A. Moore, S.C. Badescu, Simultaneous measurement of temperature, stress, and electric field in GaN HEMTs with micro-Raman spectroscopy, Rev. Sci. Instrum. 88 (2017) [CrossRef] [Google Scholar]
- P.A. Bosman, D. Thierens, The balance between proximity and diversity in multiobjective evolutionary algorithms, IEEE Trans. Evol. Comput. 7, 174–188 (2003) [CrossRef] [Google Scholar]
- S. Cheng, P.C. Chou, Novel packaging design for high-power GaN-on-Si high electron mobility transistors (HEMTs), Int. J. Thermal Sci. 66, 63–70 (2013) [CrossRef] [Google Scholar]
- A. Chvála, R. Szobolovszký, J. Kovác, Advanced characterization techniques and analysis of thermal properties of AlGaN/GaN Multifinger Power HEMTs on SiC substrate supported by three-dimensional simulation, J. Electron. Packag. Trans. ASME 141, 1–7 (2019) [CrossRef] [Google Scholar]
- K. Deb, A. Pratap, S. Agarwal, T. Meyarivan, A fast and elitist multiobjective genetic algorithm: NSGA-II, IEEE Trans. Evol. Comput. 6, 182–197 (2002) [Google Scholar]
- S.K. Dubey, K. Sinha, P.K. Sahu, Characterization of InP-based pseudomorphic HEMT with T-gate, Microsyst. Technol. 26, 2183–2191 (2020) [CrossRef] [Google Scholar]
- C. Dundar, N. Donmezer, Thermal characterization of field plated AlGaN/GaN HEMTs, InterSociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, ITHERM, 2019 May, pp. 755–760 [Google Scholar]
- A. El Hami, D. Delaux, H. Grzeskowiak, Reliability of high-power mechatronic systems 1: aerospace and automotive applications: simulation, modeling and optimization (Elsevier, 2017) [Google Scholar]
- A. El Hami, P. Pougnet, Embedded mechatronic systems 2: analysis of failures, modeling, simulation and optimization, Vol. 2 (Elsevier, 2020) [Google Scholar]
- R. El Maani, B. Radi, A. El Hami, Multiobjective backtracking search algorithm: application to FSI, Struct. Multidiscipl. Optim. 59, 131–151 (2019) [CrossRef] [Google Scholar]
- R. El Maani, S. Elouardi, B. Radi, A. El Hami, Multiobjective aerodynamic shape optimization of NACA0012 airfoil based mesh morphing, Int. J. Simul. Multidiscipl. Des. Optim. 11, 11 (2020) [CrossRef] [EDP Sciences] [Google Scholar]
- M. Florovič, R. Szobolovszký, J. Kováč, Rigorous channel temperature analysis verified for InAlN/AlN/GaN HEMT, Semicond. Sci. Technol. 34 (2019) [Google Scholar]
- J.P. Jones, E. Heller, D. Dorsey, S. Graham, Transient stress characterization of AlGaN/GaN HEMTs due to electrical and thermal effects, Microelectron. Reliabil. 55, 2634 (2015) [CrossRef] [Google Scholar]
- M.A.D. Maur et al., AlGaN/GaN HEMT degradation: an electro-thermo-mechanical simulation, IEEE Trans. Electron Devices 60, 3142–3148 (2013) [CrossRef] [Google Scholar]
- N. Moultif, O. Latry, M. Ndiaye, S-band pulsed-RF operating life test on AlGaN/GaN HEMT devices for radar application, Microelectron. Reliabil. 100, 113434 (2019) [CrossRef] [Google Scholar]
- C. Multiphysics, C. Module, Comsol multiphysics user's guide, Version, COMSOL Multiphys. 5, 3 (2019) [Google Scholar]
- S. Sadek, M. Essaaidi, O. Jardel, InAlN/GaN HEMTs based L-band high-power packaged amplifiers, Int. J. Microwave Wireless Technol. 6, 565 (2014) [CrossRef] [Google Scholar]
- S. Samira, Modeling of enhancement-mode GaN-GIT application, IEEE Trans. Electron Devices 1–7 (2020) [Google Scholar]
- L.E. Stevens, Thermo-piezo-electro-mechanical simulation of AlGaN (aluminum gallium nitride)/GaN (gallium nitride) high electron mobility transistor, 2013 [Google Scholar]
- A.A. Wilson, N.R. Jankowski, F. Nouketcha, R. Tompkins, Kapitza resistance at the two-dimensional electron gas interface, 2019 18th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), 2019, IEEE, pp. 766–771 [CrossRef] [Google Scholar]
- R. Zhang, W.-S. Zhao, W. Yin, Investigation on thermo-mechanical responses in high power multi-finger AlGaN/GaN HEMTs, Microelectron. Reliabil. 54, 575–581 (2014) [CrossRef] [Google Scholar]
Cite this article as: Abdelhamid Amar, Rabii El Maani, Bouchaïb Radi, Abdelkhalak El Hami, Multi-objective optimization of the high electron mobility transistor, Int. J. Simul. Multidisci. Des. Optim. 14, 16 (2023)
All Tables
All Figures
 |
Fig. 1 Structure of the HEMT technology. |
| In the text | |
 |
Fig. 2 Evolution of the operating temperature as a function of the dissipated power. |
| In the text | |
 |
Fig. 3 Distribution of the von Mises stresses. |
| In the text | |
 |
Fig. 4 Variation of the von Mises stresses. |
| In the text | |
 |
Fig. 5 Flowchart of the coupling process. |
| In the text | |
 |
Fig. 6 Pareto solutions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.