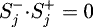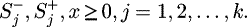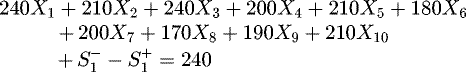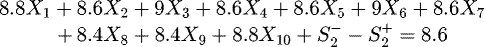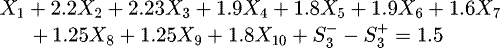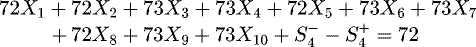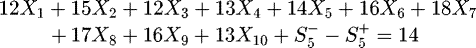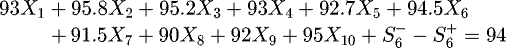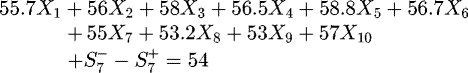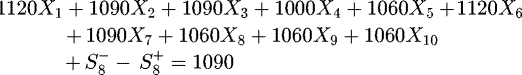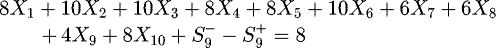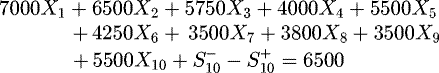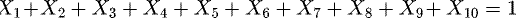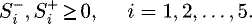| Issue |
Int. J. Simul. Multidisci. Des. Optim.
Volume 12, 2021
Advances in Modeling and Optimization of Manufacturing Processes
|
|
|---|---|---|
| Article Number | 8 | |
| Number of page(s) | 11 | |
| DOI | https://doi.org/10.1051/smdo/2021008 | |
| Published online | 24 June 2021 | |
Research Article
Binary goal programming model for optimizing tire selection using branch and bound algorithm
Assistant Professor, Faculty of Engineering at Helwan, Helwan University
* e-mail: shady_ali@h-eng.helwan.edu.eg
Received:
12
January
2021
Accepted:
13
May
2021
The problem of assessment and adoption of automotive tyre design specifications has not been addressed sufficiently in literature. This is in spite of its significance as a crucial component relevant to design and safety of the automobile. In this paper, a multi-objective optimization model of the tyre design trademark adoption decision is proposed. Multi-attribute or multi-criterion decision making techniques are heuristics providing good solution, but do not guarantee optimum solution. Up to date, there is no optimal yielding method for selection of vehicle tyre manufacturer or trademark based on prespecified design targets. The proposed model is formulated as a binary goal programming model for optimizing tyre trademark design selection decision by adopting an optimal tyre design trademark that best achieve design targets. The model is solved by the branch and bound algorithm. One advantage of the proposed model is flexibility to incorporate multiple design targets, tolerance limits and different constraints. The proposed model can support efficient and effective decision making concerning the adoption of tyre trademark design for new automobile or to re-adopt new design for new road vehicle operating conditions.
Key words: Tyre designs / tyre trade-mark selection / binary goal programming / integer programming / branch and bound (B&B)
© S. Aly, Published by EDP Sciences, 2021
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Tyres are one of the most important parts of a vehicle as they represent the only connection between the automobile and the road surface. Hence, it is essential to adopt a specific tyre manufacturer or trademark such that they enhance the acceleration, braking and handling quality of the automobile vehicle. The fuel efficiency is also improved with good quality tyre. On the other hand, cheap, low quality tyre can give you an unpleasant and bumpy ride and even can jeopardize the safety of the driver. Indeed, tyre is a very crucial component. It has a significance impact on the performance of the vehicle other components as well as on the safety of the automobile on the road. Automobile's designers usually seeks improvement of their design's competitiveness through optimizing design attributes, while minimizing associated costs.
Nowadays', in the market, there is a wide spectrum of tires available for various models and styles of automobiles. Therefore, the consistency and justification of tyre choice decision is an important and a crucial issue. In order to select appropriate tyre design, the automobile manufacturer has to select adequate tyre standard size including: tread width, percentage tread height, tyre radius, wheel diameter, load index and speed rating of the tyre. Additional criteria depending on significance to the design may include, cushioning, dampening, braking torque, rolling resistance, and expected life span [1–3].
An automobile designer has to ensure that the selected tyre manufacturer (i.e., trade-mark) among the available alternatives) complies among the other alternatives with the prospective automobile's desired performance based on availability of pre-specified set of tyre design attributes.
In fact, literature on tyre trade-mark or standardized design specification selection is very rare. Most research on tyre were related to studying the tyre properties on tyre performance. For instance, Ratrout in 2005 [4] & 2006 [5] highlighted that elongation and tensile strength of the tyre are important quality control criteria in vehicles road performance evaluation. A field investigation of eight different brands of tires to understand the reasons for tyre failure was reported in Ratrout [4]. Boodihal et al. [6] further assessed the tyre noise on the road. Other researchers focused on the impact of tyre failure on road accidents and reported a significant impact. Tire blowouts are extremely a safety issue concern. Ratrout [7] reported that close to 13% of road accidents reported are attributed to tire failure. Carcaterra and Roveri [8] introduced a technique for identification of tire grip based on utilizing strain information inside the tire. Using the tire' strain information, relevant characteristics of the tire-road contact can be extracted. Weyssenhoff et al. [9] investigated the characteristics of selected passenger car tires' manufacturing defects. They analysed samples of tires' defects and causes occurred during manufacturing process. Pattanaik and Balu [10] studied the effect of plus size tire on vehicles performance. They aimed to demonstrate how the plus-size pneumatic affects all vehicle's performance as well as its stability. Mousavi & Sandu (2020) [11] developed a theoretical model for the study of the performance of tire on ice. They validated the model using experimental results for three similar tires with different rubber compounds properties. They concluded that the developed model can be used to predict the temperature changes at the contact patch, the tire friction force, the of wet and dry regions' areas, the height of the water film for different ice temperatures, different normal load, etc. He et al. (2021) [12] presented an a laboratory based experimental study of the tire tractive performance on soft soils. They stated that the research findings can be considered groundwork for tire off-road dynamics and the development of traction controllers for vehicles on soft soil. Concerning tire loading performance, Cosseron et al. [13] proposed an optimization technique of the wheel instrumentation, to minimize the uncertainties of the sought parameters during the tire-trim loading identification process. Kang et al. [14] utilized the discrete element method (DEM) to study the performance of discarded off-the-road (OTR) tire chips under compression. Concerning tire speed rating and rolling resistance, Gao et al. [15] presented a technique 3D digital imaging correlation for measuring tire rolling resistance coefficient for high-speed running tire. Gao et al. [16] introduced a modeling and experimentation of tire deformation characteristics as a result of high speed rolling conditions. Research on tire tread depth focused on the impact of tread depth and tread pattern on the tire performance. Particularly, they addressed the influence of tread pattern on tire noise. Concerning the tire noise, Wang [17] presented an analysis, measurement and simulation on automotive tire noise and vibration. They considered tire noise issues from tire structure and from the whole vehicle. Chen et al. (2021) [18] utilized the Bayesian analysis to model and study the influential factors that impact tire − pavement noise. Among the significant findings are that the tire/pavement noise increases with macrotexture depth while decreases with the porosity of the surface material. The porous asphalt pavement attenuates noise more significantly at a higher speed. The noise level increases statistically when the tire load increases, while it decreases as the air temperature increases. Concerning tire grip or traction, Cutini et al. (2020) [19] assessed the performance drawbacks of 17.5 R25 sized industrial winter tires. presents a method for testing winter tires in outdoor test facilities with a focus on traction performance. Mohammadi and Ohadi [20] presented a new approach to design of quiet tires, using multi-objective minimization of generated noise. They focused on designing tires with low-noise level and help manufacturers based upon scientific insights.
Closely related to this research and one of the rare attempt to implement multi-criteria decision making is the work Ateekh-Ur-Rehman & Alkahtani [21], who presented an approach for assessing of automobile tires alternatives taking into account multiple criteria, such as tyre sustainability, tire road performance, environmental issues, tire purchase cost and tire road grip. They stated that the presented approach helps to not only in ranking alternatives but also in establishing the superiority of an alternative over others.
The above literature indicate that the problem of assessing tyre's design specifications selection has not been sufficiently addressed in the literature, except for very few attempts mentioned above and only based on assessing several alternatives, and considering optimizing the decision for specific design target related to the automobile design, and which represent one limitation of reliance on multicriteria decision alone in this selection process and without optimizing the decision to arrive at best solution from the perspective of target design. It is obvious that there is no methodology exists to optimize tyre design selection.
Therefore, based on the above outcome, it is a worthy to have more reliable and efficient a method that optimize the decision of tyre design selection. Tyre trade-mark manufactures offers several tyre design specifications for common tyre design attributes such as: tread depth, max speed, rolling resistance, grip or both wet and dry conditions. The common issue here is which trademarks to select based on some given target design specifications depending on the design of the vehicle and its adequate tyre design. This should be based on the adopting the closest tyre trademark specifications to the target tyre design specification required. However, there is still another selection factor which is the cost of the tyre trademark. This means that optimization is necessary to help adopt the optimal tyre design trademarks offering.
In fact, multi-criterion decision making methods, in spite of wide use in decision making problems, these methods are not sufficient without mathematical programming that help optimizing the final outcome. Instead, this research proposes a binary goal programming optimization model that enables adopting the optimal tyre trademark that has identical or closest design specification that yield the minimum deviation from the required tyre design specifications targets, while minimizing the cost as an important goal. This one major advantage of goal programming approach that help achieve several conflicting goals which optimizing the realization several constraints, such as the cost. Over and above, the proposal of utilizing binary version of goal programming is naturally ensuing from the fact that the decision to whether adopt a specific tyre design trademark is a binary: “Yes” or “No”. The proposed approach is inspired by real case of designing first Arab, Saudi Car, Gazal (Fig. 1).
Therefore, this research presents a binary goal programming (GP) model for optimizing the selection decision of automobile tyre designs. The GP optimization have been utilized before successfully to deal with multi-objective and multi-criterion decision making problems. Chang (2007) [22] presented a binary fuzzy goal programming model and solved it using the integer programming method. Jayaraman et al. (2015) [23] proposed a weighted goal programming model that integrates efficient allocation of resources to simultaneously achieve sustainability related goals. Rubem et al. (2017) [24] proposed weighted goal programming (GP) approaches were to solve the multi-criterion data envelopment analysis (MCDEA) to tackle the issue of lack of discrimination power model. Broz et al. (2019) [25] presented a formulation for the optimal planning of the daily production of sawmills. They solved the problem using a Goal Programming approach allowing different criteria to be weighted. Amin et al. [26] presented combined goal programming and inverse data envelopment analysis (DEA) method for target setting in mergers and applied to banking industries. Ho (2019) [27] presented two methods of multi-objective decision making, Weighted multi-choice goal programming (MCGP) and MINMAX MCGP. The compared the two methods on the manufacturing company's problem of selecting suppliers based on multiple objectives and different weights. They used fuzzy numbers to express goals satisfaction and weights estimation. Al-Husain and Khorramshahgol [28] propose a supply chain (SC) design methodology. They combined the analytical hierarchy process (AHP) with weighted binary goal programming (GP), in a two-stage approach to design a SC. At the initial stage, the AHP used to develop weights for the individual SC drivers. The GP model is used to determine the optimal set of SC-driver decisions for developing the overall satisfactory SC design.
This paper is organized as follows. Section 2 introduces the tyre standards, designations codes that are essential to identify tyre selection criteria and requirements. Section 3 will introduce the common selection attributes of the automobile tyre design trademark. In Section 4, the input data of the tyre design trademarks are introduced. Section 5 presents the basic constituents of the binary goal programming model for the tyre selection optimization problem. In Section 6, the conclusion is presented. in Section 6.
 |
Fig. 1 Gazal automobile design. |
2 Tyre standards and identification codes
Several well-known international tire standards exist and influence the tire design specifications undertaken all over the world. International tire technical standards and regulations includes:
DOT code is an alphanumeric character sequence molded into the sidewall of the tire and allows the identification of the tire and its age. The code is mandated by the U.S. Department of Transportation (49 CFR 574.5 − Tire identification requirements.), but this code is used worldwide.
In the United States, the Office of Vehicle Safety Compliance, a component of the Department of Transportation, is one of the agencies tasked to enforce the Federal Motor Vehicle Safety Standard (FMVSS). Canada has published tire regulations, such as the Motor Vehicle Tire Safety Regulations SOR 95–148.
All tires sold for road use in Europe must carry an E-mark. An (upper case) “E” indicates that the tire is certified to comply with the dimensional, performance and marking requirements of ECE regulation 30.
Automotive tires are designated by an alphanumeric tire code, which is generally engraved or molded into the tire's sidewall. The ISO metric tire code is composed of a string of letters and numbers to indicate various design specifications parameters of the tire including tire sizes, speed rate, tread depth, wet and dry grip grades, etc. (See tire code indications in Fig. 2).
Based on study of tire standards and codes, nine key tyres design specifications were identified, and upon which this research study will consider as key tire selection attributes focus. They are: max speed rating, tread depth, rolling resistance, dry and wet grip or traction, noise pollution, carrying load, long lasting and cushioning.
Sections 3 will define the most significant tire selection attributes or criteria.
 |
Fig. 2 Tire identification codes. |
3 Tyre selection attributes
The selection attributes and of the automobile tyre manufacturers and their ranges of values are defined and explained in this section (See Fig. 3). They are as follows:
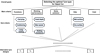 |
Fig. 3 Tyre manufacturers selection attributes. |
3.1 Function (C1)
Involves tyre functionalities related to guaranteeing safety, comfort and durability attributes. The function includes carrying, cushioning and long lasting:
3.1.1 Carrying (C11)
Measures the ability of the tyre to support vehicle load during acceleration and braking. Normally the tyre can carry about 50 times its weight.
Mostly, the maximum load the tyre can carry ranges from 800 to 1250 kg.
3.1.2 Cushioning (C12)
The ability of the tyre to absorb the shocks due to the obstacles, surface roughness and irregularities confronted by the car on the road. The cushioning is expressed qualitatively from very poor to very good cushioning degree, and can quantitatively expressed between 0 and 10, respectively, with center values for five grade levels, as indicated in the Table 1.
3.1.3 Lasting (C13)
The ability of the tyre to keep their optimum working performance level for millions of wheel revolutions. The tyre wear is affected by its use conditions: load, speed, state of road surface, state of vehicle, and driving style.
The tyre lasting ranges from 1 to 2.25 years for most known tyre trademarks.
3.2 Working performance (C2)
The performance of the tyre is affected my multiple factors. They are defined below.
3.2.1 Max speed (C21)
Tyre speed rating is usually denoted by letters of alphabets from A to Z. as the speed increases, and has a corresponding kilometers/hours values.
The speed rating in Kilo-meters per hours (km/h) has been studied for about ten trade marks, where the maximum speed the tyre can reach without damage have been decoded and found to be within the range 180–270 km/h.
3.2.2 Tread depth (C22)
Tread patterns in general is responsible for the performance of your car in different weather conditions. They are responsible for channeling the water away when you are driving through a water-logged area. The depth of tread is very significant safety factor of the tyre, since it affects the stopping distance in wet, and in gripping when cornering. The legal tread depth limit is 1.6 mm, but for greater safety in wet condition, the tyre is recommended to be changed at 3 mm.
Usually, the tread depth of the manufactured tyre ranges from 7 to 9 mm, and it is desirable to have maximum tread depth.
3.2.3 Rolling resistance (C23)
Rolling resistance is defined as a measurement of how easily (or not) a tyre rolls down the road. The higher rolling resistance of a tyre, the greater the power requirements to propel in motion, which in turn leads to larger levels of fuel consumption.
Expressed in percentage (% of resistance), a range from 10% to 20% is defined and used by the tyre manufacturers to express the degree of rolling resistance. Typically, a minimum rolling resistance is preferred.
3.3 Noise pollution (C3)
Tyre noise is produced by the tyre while running on a ground surface. Every tyre pattern has a particular level of tyre noise. For instance, the tyre noise level of rib tyre is much lower than that produced by lug or block tyre. Cars with light load have a lower noise level than that of heavy load, etc.
The tyre manufacturer usually expresses the tyre noise in terms of a percentage, and for common tyre manufacturers, it ranges from 68 to 76 decibel (dB). It is desirable to have minimum noise level.
3.4 Grip (C4)
The grip or traction criterion or tyre property is very essential in braking and cornering. A grip of tyre is important for a car to turn or advance. If tyre grip does not exist, then the cars would just spin in a one place. In fact, grip is synonymous with safety. The grip properties of car tyre in dry surfaces are different from grip on wet surface.
3.4.1 Grip on dry surface (C41)
Grip on dry surface has two aspects for which forces of grip differ:
Micro roughness (a few angstroms) brings into play molecular forces of grip, and occurs on smooth surfaces.
Macro roughness (a few microns to a few millimeters) brings into play very significant forces of grip.
Tyre grip on dry surface is expressed in term of % of tyre performance. Typically, higher percentage are preferred. The tyre trademarks grip on dry surfaces ranges from 88% to 96%.
3.4.2 Grip on wet surface (C42)
Grip on wet surface has two aspects for which forces of grip differ:
Visco-planting is due presence of a residual film of water between the road surface and the tyre, where water level is less than 0.5 mm. In this case, grip tends to be zero and sliding cannot be stopped.
Aqua-planting is the progressive loss of contact with the ground on account of the formation of a sheet of water between the tyre and the ground, where the water level is greater than 0.5 mm, and as a result of speed of the vehicle.
Tyre grip on wet surface is expressed also in term of % of tyre performance. Typically, higher percentage of tyre performance on we surface is preferred. The tyre trademarks grip on wet surfaces ranges from 50% to 60%.
3.5 Cost (C5)
The tyre cost represents the tyre purchase price and all necessary processing and installation expenditures. Tyre cost specified for the four wheels ranges from 1800 to 9000 Egyptian pound.
The above attributes and properties are relevant to the tyre selection, and this research, it is sought to present a model that achieve the following aims:
Optimize the values of the above attributes, properties and/or judgment criteria in such a way that the target values of the above criteria are achieved as goals.
Handle multiple goals, concerning the optimum levels of technical attributes, while minimizing the associated cost as resulting outcome of the selection achieving Provision for handling trade-off between benefit-based criteria and cost-based criteria.
Handle the associated vagueness inherent with assessing the qualitative subset of the criteria.
The problem now can be stated as follows:
“Given a set of tyre manufacturers trade-marks alternatives A = {a1, a2, …, ai, .., am}, and the given the selection attributes C = {c1, c2, …, cj, .., ck}, it is required to select the optimum tyre manufacturer, that achieve a set of pre-specified target attributes values simultaneously, where the desirability is to achieve a target attribute value is defined either as approximately equal (=), approximately greater than or equal (≥) or approximately less than or equal (≤)”.
In the next section, the input data of the tyre selection optimization problem are defined.
4 Tyre designs data
The desired tyre size is 255/55 R20 110V, with maximum speed equal to 240 km/h, however, the lower limit for the maximum speed is 200 km/h. The collected input data [21] about tyre selection attributes include the measured key attributes values for nine attributes, defined in previous sections. The studied data are for ten well-known tyre manufacturers. Table 2 shows the mean attribute values for 9 attributes and for the ten tyre manufacturers. Table 3 gives the average tyre cost for the size 255/55 R20 110V.
The target design values or goals of each tire Selection attribute of the Gazal automobile tires are indicated in Table 4 below.
Next section, the goal programming model of the tyre manufacturer selection optimization is presented.
Cushioning grade and corresponding quantified value.
Tyre selection attribute values for 10 tyre manufacturers.
Average tyre cost for the size 255/55 R20 110V.
Goals for tyre selection attribute.
5 Binary goal programming model for tyre selection optimization
5.1 Goal programming model
In this section, the goal programming model is presented. The goal programing commonly known with the goal values, that are the right-hand sides of the defined goals inequalities. The simple additive or weighted sum goal programming model is defined as for k number of goals, Gj(x), with deviational variables:  :
: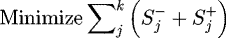
where: gj represents the target level of the j-th goal.
In fact, the utilization of goal programming in tyre design trademark selection offers several advantages. One of these advantages is its ability to handle realistic conflicts in goals influencing the decision process. Also, goal programming enables use of deviational variables for suiting different requirements of vehicle designs, while through design tolerance limits validity can still be guaranteed. Further, the problem of tyre design trademark optimization is more conveniently modeled using binary variables, the proposal of utilizing binary version of goal programming is naturally ensuing from the fact that the decision to whether adopt a specific tyre design trademark is a binary: “Yes” or “No”. Therefore, the binary goal programming modeling of the tyre design trademark selection is considered adequate, based on the nature of decision problem's variables conflicting goals, constraints, etc.
Now, the branch and bound approach that is widely used for solving binary integer program is computationally efficient option for optimizing the tyre design election decision.
Next section reviews the basic steps of the branch and bound algorithm.
5.2 The branch and bound algorithm
Branch and bound (B&B) techniques have proven very successful in many applications due to its high capability to reduce the search space and exhibit a high computational efficiency. B&B algorithms have been implemented extensively in many applications in the literature. Due to its computational efficiency, its utilization continues widely. Among recent application is the development of a combinatorial Branch and bound for the common Knapsack problem [29]. Gmys et al. (2020) [30] developed a B&B algorithm for optimizing the permutation flow-shop scheduling problem, with make span objective. Theurich et al. [31] applied a branch and bound approach to the scheduling of tamping actions in railway. They modeled the problem as is a vehicle routing optimization. Becker et al. (2018) [32] addressed the tire noise optimization problem. They presented a mixed integer linear program for solving the non-linear tire noise optimization using branch and cut approach.
The algorithmic steps is stated as follows:
Initialization: Set an initial lower bound Z* = −∞, for a maximization problem (Z* = +∞, for a minimization problem), on the optimum objective value of integer. Set i = 0.
Step 1. (Fathoming/bounding). Select a linear program (LPi), the next subproblem to be examined. Solve LPi, and fathom it using one of three conditions:
The optimal objective function's value of LPi (i.e., Zi) cannot yield a better value than the current lower/upper bound (i.e., Zi ≤ Z* in case of max. and Zi ≥ Z*, in case of minimization).
LPi yields a better feasible integer solution than the current lower bound/upper bound.
LPi has no feasible solution.
Two outcomes can arise:
If LPi is fathomed and a better solution is found, update the lower/upper bound. If all subproblems have been fathomed, stop; the optimum ILP is associated with the current finite lower/upper bound. If no finite lower bound exists, the problem has no feasible solution. Else, set i = i + 1, and repeat step 1.
If LPi is not fathomed, go to step 2 for branching.
Step 2. (Branching). Select one of the integer variables Xj, whose optimum value Xj* in the LPi solution is not integral. Eliminate the region [Xj*] < Xj < [Xj*] + 1 (where [µ] defines the largest integer ≤µ) by creating two LP subproblems that correspond to:
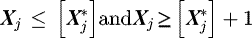
Set i = i + 1, and go to step 1.
5.3 Formulating and solving the tyre manufacturer selection optimization
The following is the definition of the decision variable, goal inequalities, constraints and the deviational variables. Then the final complete goal programming model for tyre trade-mark selection optimization will be formulated as follows: −
5.3.1 Defining decision variables
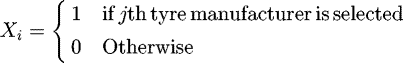 where: I = 1,2,…,10. The index 1 refers to tyre manufacturer “Toyo”, and so on. It should be noted that the cost attribute is the 10th index.
where: I = 1,2,…,10. The index 1 refers to tyre manufacturer “Toyo”, and so on. It should be noted that the cost attribute is the 10th index.
5.3.2 Formulating goal inequalities
The tyre selection goals are expressed in form of inequalities as follows:
Goal 1: Attain the target Maximum speed goal:
240 X1 + 210 X2 + 240 X3 + 200 X4 + 210 X5 + 180 X6 + 200 X7 + 170 X8 + 190 X9 + 210 X10 ≥ 240
Goal 2: Attain the target Tread depth goal:
8.8 X1 + 8.6 X2 + 9 X3 + 8.6 X4 + 8.6 X5 + 9 X6 + 8.6 X7 + 8.4 X8 + 8.4 X9 + 8.8 X10 ≥ 8.6
Goal 3: Attain the target Long Lasting goal:
1.5 X1 + 2.2 X2 + 2.23 X3 + 1.9 X4 + 1.8 X5 + 1.9 X6 + 1.6 X7 + 1.25 X8 + 1.25 X9 + 1.8 X10 ≥ 1.5
Goal 4: Attain the target Noise Pollution goal:
72 X1 + 72 X2 + 73 X3 + 73 X4 + 72 X5 + 73 X6 + 73 X7 + 72 X8 + 73 X9 + 73 X10 ≤ 72
Goal 5: Attain the target Rolling Resistance goal:
12 X1 + 15 X2 + 12 X3 + 13 X4 + 14 X5 + 16 X6 + 18 X7 + 17 X8 + 16 X9 + 13 X10 ≤ 14
Goal 6: Attain the target Dry surface goal:
93 X1 + 95.8 X2 + 95.2 X3 + 93 X4 + 92.7 X5 + 94.5 X6 + 91.5 X7 + 90 X8 + 92 X9 + 95 X10 ≥ 94
Goal 7: Attain the target Wet surface goal:
55.7 X1 + 56 X2 + 58 X3 + 56.5 X4 + 58.8 X5 + 56.7 X6 + 55 X7 + 53.2 X8 + 53 X9 + 57 X10 ≥ 54
Goal 8: Attain the target Carrying load goal:
1120 X1 + 1090 X2 + 1090 X3 + 1000 X4 + 1060 X5 + 1120 X6 + 1090 X7 + 1060 X8 + 1060 X9 + 1060 X10 ≥ 1090
Goal 9: Attain the target Cushioning rate goal:
8 X1 + 10 X2 + 10 X3 + 8 X4 + 8 X5 + 10 X6 + 6 X7 + 6 X8 + 4 X9 + 8 X10 ≥ 8
Goal 10: Attain the target Cost limit goal:
7000 X1 + 6500 X2 + 5750 X3 + 4000 X4 + 5500 X5 + 4250 X6 + 3500 X7 + 3800 X8 + 3500 X9 + 5500 X10 ≤ 6500.
5.3.2.1 Constraints
Constraint 1: The goal programming optimization model must yield only one tyre manufacturer best satisfying all goals: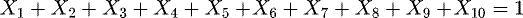
Constraint 2: The decision variables possible values: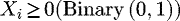
5.3.3 Introducing deviational variables
The goal programming model is formulated essentially by defining deviational variables that defines magnitudes of realizations of individual goals for each selection attributes. Then solved by minimizing the model, while minimizing the magnitudes of these deviation, and considering all other logical constraints, as indicated below.
Objective function:

5.3.4 The branch and bound solution of the binary goal programming model for tyre manufacturer selection optimization
The B&B solution of the integer programs is applied to the above binary goal programming formulation of tyre selection optimization model. The B&B tree is illustrated in Figure 4.
As shown in Figure 4, the B&B solution procedure is followed. The solution of the first node yields objective value Z = 1.26, representing the measure of overall deviations from goals attainments, and unfeasible value of the variable X1 is unfeasible because it is non-integer. This requires further branching. The solution procedure continues until finding an integral value for the objective function, that is to be set as an upper bound. Solutions branches are fathomed either they are integral solution, or they lead to no feasible solution. This occurred at node 3, with an objective value equal 51. The final optimal solution occurred at node or iteration 10, with an objective value equal 49.5. The solution variables values are:
Z* = 49.5
X1 = 0, X2 = 0, X3 = 0, X4 = 0, X5 = 0, X6 = 0, X7 = 1, X8 = 0, X9 = 0, X10 = 0.
(Integral solution).
The final optimal solution results are obtained and are shown below.
The optimal solution is found after 10 iterations, with an objective value equal z = 49.5 and the optimal tyre alternative selected is “T07” (X7 = 1).
-
The detailed results on the model deviational variables are illustrated in Table 5, below.
Table 5B&B solution results for binary goal program of the tyre selection optimization.
Table 5 shows the values of the deviational variables' values for each goal tyre trademark alternatives expressed as selection variables with values ether 0 or 1, based on either selected or not. The tables yields as well the deviational. It clear from Table 5, that the optimal decision is to adopt the T07 tyre manufacturer trademark, as it has the lowest overall possible deviations from the target design values.
The implementing the B&B yielded the following results, based on the deviational values on the goals:
The optimal solution attained through applying the B&B algorithm to the tire selection goal programming model is validated against the lower and upper bound limits according to attribute type case (i.e., either maximization or minimization, respectively). In spite of the existing deviations in the values of the goals which is usually the nature of the goal programming model, it is obvious from Table 6 that all deviations are within lower or upper limits or tolerance, which is acceptable.
 |
Fig. 4 B&B tree for tire selection optimization. |
B&B optimal solution for the tyre selection validated against the tire specification tolerance limits.
6 Conclusion
A binary goal programming model is used to model and solve the problem of tyre design trademark selection optimization. Due to the lack of methodologies to select tyre design trademarks manufacturer, given pre-specified target design values attributes, the proposed solution methodology that yields an optimal tyre selection solution represent a great contribution to this research area. The proposed methodology has an obvious advantage over the multi-criterion decision making methods in that it is guaranteed to yield the optimal solution, especially in case of conflicting goals. The disadvantages of multi-criterion decision making are that they have no means to handle or compromise conflicts in goals, design tolerance limits and slight deviations in design from target goals' values. Goal programming approach is also suited when the target design slightly differs from the offered alternative's design attributes, and that slight deviations from the target design levels are permitted with a prespecified tolerance limits.
In this research, we have applied the binary goal programming model to optimize the tyre design trademark selection decision of the Saudi Gazal car. the model has been solved by the B&B solution algorithm. The obtained optimal solutions include the identification of the optimal design trademark. The solution has been validated using the tyre design tolerance limits, since all the slight deviations of the goal program were inside the design tolerance limit.
The presented methodology is transparent and displays the deviation from target design specifications, where it is difficult to satisfy conflicting objectives simultaneously, and it is not common to find a specific tyre manufacturer design exactly equal to the tyre target design attributes. Finally, the presented methodology is practical and computationally efficient.
7 Implications and influences
The presented article will pave the road towards several subsequent research. It has introduced a structured analysis and building blocks of research prototype for optimization of the tyre designs selection. It has structured the design criteria, built the goals based on their values and eventually formulate the problem logically into a binary multi-objective goal programming optimization model, which is solved efficiently using the branch and bound algorithm.
This novel research necessarily will compensate for the scarcity of contributions to this important design element of the civil automobiles. Due to the lack of treatment and approaches for tyee design optimization, the proposed article is particularly valuable in its scientific contribution and future implications and influences. The interested researchers have now starting point to launch new research under varying requirements and constraints. In the other hand, practitioners of course have a reliable methodology to manage and optimize the tyre design adoption decision.
References
- B. Rodgers, W. Waddell, Tire engineering science and technology of rubber, Science and Technology of Rubber (Elsevier, 2005) [Google Scholar]
- M.J.L. Boada et al., Neuralempirical tire model based on recursive lazy learning under combined longitudinal and lateral slip conditions, Int. J. Automotive Technol. 12, 821–829 (2011) [CrossRef] [Google Scholar]
- R.S. Vieira, L.C. Nicolazzi, N. Roqueiro, Four-wheel vehicle kinematic and geometric constraints for definition of tire slip angle, Int. J. Automotive Technol. 13, 553–562 (2012) [CrossRef] [Google Scholar]
- N.T. Ratrout, Tire condition and drivers practice in maintaining tires in Saudi Arabia, Accid. Anal. Prevention 37, 201206 (2005) [CrossRef] [Google Scholar]
- N.T. Rarout, I.A. Mahmoud, Adequacy of the tensile/elongation test as a quality control criterion for vehicle tires, Polymer Test. 25, 588–596 (2006) [CrossRef] [Google Scholar]
- M.A. Boodihal et al., Development of tire/road noise assessment methodology in India, Case Stud. Constr. Mater. 1, 115–124 (2014) [Google Scholar]
- N.T. Ratrout, Evaluation of passenger car tire fgailure in Saudi Arabia, Arab. J. Sci. Eng. 36, 749–760 (2011) [CrossRef] [Google Scholar]
- A. Carcaterra, N. Roveri, Tire grip identification based on strain information: theory and simulations, Mech. Syst. Signal Process. 41, 564–580 (2013) [CrossRef] [Google Scholar]
- A. Weyssenhoff et al., Characteristics and investigation of selected manufacturing defects of passenger car tires, in: 13th International Scientific Conference on Sustainable, Modern and Safe Transport (TRANSCOM 2019), High Tatras , May 29–31, 2019, Novy Smokovec − Grand Hotel Bellevue, Slovak Republic [Google Scholar]
- P.P. Pattanaik, V. Balu, Plus size tire: effect on the performance of the vehicle, Mater. Today: Proc., available online 28 April 2021 [Google Scholar]
- H. Mousavi, C. Sandu, Tire-ice model development for the simulation of rubber compounds effect on tire performance, J. Terramech. 91, 97–115 (2013) [CrossRef] [Google Scholar]
- R. He, C. Sandu, M.N. Shenvi, H. Mousavi, J. Carrillo, J.E. Osorio, Laboratory experimental study of tire tractive performance on soft soil: towing mode, traction mode, and multi-pass effect, J. Terramech. 95, 33–58 (2021) [CrossRef] [Google Scholar]
- K. Cosseron et al., Optimized gauging for tire–rim loading identification, Eur. J. Mech.A/Solids 87, 104192 (2021) [CrossRef] [Google Scholar]
- C. Kang, S. Huang, A. Bayat, Compressibility characteristics of TDA from OTR (off-the-road) tires: a numerical approach, Transport. Geotech. 29, 100561 (2021) [CrossRef] [Google Scholar]
- X. Gao, Y. Zhuang, S. Liu, High-speed 3D digital image correlation for measuring tire rolling resistance coefficient, Measurement 171, 108830 (2021) [CrossRef] [Google Scholar]
- X. Gao et al., Modeling and experimental study of tire deformation characteristics under high-speed rolling condition, Polymer Test. 107052 (2021) [CrossRef] [Google Scholar]
- X. Wang, Automotive Tire Noise and Vibrations, 1st edn., Analysis, Measurement and Simulation, (Butterworth-Heinemann, (2020) [Google Scholar]
- L. Chen, L. Cong, Y. Dong, G. Yang, B. Tang, X. Wang, H. Gong, Investigation of influential factors of tire/pavement noise: a multilevel Bayesian analysis of full-scale track testing data, Constr. Build. Mater. 270, 121484 (2021) [CrossRef] [Google Scholar]
- M. Cutini, M. Brambilla, P. Toscano, C. Bisaglia, G. Abbati, G. Meloro, Evaluation of drawbar performance of winter tyres for special purpose vehicles, J. Terramech. 87, 29–36 (2020) [CrossRef] [Google Scholar]
- S. Mohammadi, A. Ohadi, A novel approach to design quiet tires, based on multi-objective minimization of generated noise, Appl. Acoustics 175, 107825 (2021) [CrossRef] [Google Scholar]
- A.-U. Rehman, M. Alkahtani, Automobile tire assessment: a multi-criteria approach, Eng. Technol. Appl. Sci. Res. 7, 1363–1368 (2017) [CrossRef] [Google Scholar]
- C.-T. Chang, Binary fuzzy goal programming , Eur. J. Operat. Res. 180, 29–37 (2007) [CrossRef] [Google Scholar]
- R. Jayaraman, C. Colapinto, D. Torre, T. Malik, Multi-criteria model for sustainable development using goal programming applied to the United Arab Emirates, Energy Policy 87, 447–454 (2015) [CrossRef] [Google Scholar]
- A.P. dos Santos Rubem, J.C.C.B. Soares de Mello, L.A. Meza, A goal programming approach to solve the multiple criteria DEA model, Eur. J. Oper. Res. 260, 134–139 (2017) [CrossRef] [Google Scholar]
- D. Broz, N. Vanzetti, G. Corsano, J.M. Montagna, Goal programming application for the decision support in the daily production planning of sawmills, Forest Policy Econ. 102, 29–40 (2019) [CrossRef] [Google Scholar]
- G.R. Amin, S. Al-Muharrami, M. Toloo, Combined goal programming and inverse DEA method for target setting in mergers, Expert Syst. Appl. 115, 412–417 (2019) [CrossRef] [Google Scholar]
- H.-P. Ho, The supplier selection problem of a manufacturing company using the weighted multi-choice goal programming and MINMAX multi-choice goal programming , Appl. Math. Modell. 75, 819–836 (2019) [CrossRef] [Google Scholar]
- R. Al-Husain, R. Khorramshahgol, Incorporating analytical hierarchy process and goal programming to design responsive and efficient supply chains, Oper. Res. Perspect. 7 (2020) [Google Scholar]
- S. Coniglio, F. Furini, P.S. Segundo, A new combinatorial branch-and-bound algorithm for the Knapsack Problem with Conflicts, Eur. J. Oper. Res. 289, 435–455 (2021) [CrossRef] [Google Scholar]
- J. Gmys, M. Mezmaz, N. Melab, D. Tuyttens, A computationally efficient Branch-and-Bound algorithm for the permutation flow-shop scheduling problem, Eur. J. Oper. Res. 284, 814–833 (2020) [CrossRef] [Google Scholar]
- F. Theurich, A. Fischer, G. Scheithauer, A branch-and-bound approach for a Vehicle Routing Problem with Customer Costs, EURO J. Comput. Optimiz. 9, 100003 (2021) [CrossRef] [Google Scholar]
- M. Becker, N. Ginoux, S. Martin, Z. Roka, Tire Noise Optimization Problem: A Mixed Integer Linear Program Approach, CoRR abs/1809.05058 (2018) [Google Scholar]
Cite this article as: Shady Aly, Binary goal programming model for optimizing tire selection using branch and bound algorithm, Int. J. Simul. Multidisci. Des. Optim. 12, 8 (2021)
All Tables
B&B optimal solution for the tyre selection validated against the tire specification tolerance limits.
All Figures
 |
Fig. 1 Gazal automobile design. |
| In the text | |
 |
Fig. 2 Tire identification codes. |
| In the text | |
 |
Fig. 3 Tyre manufacturers selection attributes. |
| In the text | |
 |
Fig. 4 B&B tree for tire selection optimization. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.