| Issue |
Int. J. Simul. Multisci. Des. Optim.
Volume 5, 2014
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 14 | |
| DOI | https://doi.org/10.1051/smdo/2014001 | |
| Published online | 14 March 2014 | |
Article
Evolutionary numerical simulation approach for design optimization of gas turbine blade cooling channels
Department of Industrial Engineering and Management Systems, University of Central Florida, Orlando, Florida
32816, USA
* e-mail: raju@ucf.edu
Received:
10
November
2013
Accepted:
13
January
2014
Gas turbine blade cooling system design is a multidisciplinary, iterative and often tedious task involving complex relationships among multiple design objectives. Typical blade design requires a broad range of expertise in the materials, structural, heat transfer, and cost optimization disciplines. The multiple objectives involved are often conflicting and must be solved simultaneously with equal importance. The traditional approaches researchers scalarize the multiple objectives into a single objective using a weight vector, thus transforming the original multiple objective problem into a single objective problem. This research addresses the shortcomings of existing traditional approaches of the optimization of blade cooling configuration design.
Key words: Multiobjective / Optimization / Evolutionary / Numerical simulation / Gas turbine / Blade cooling channel / Ribs
© N.R. Nagaiah, C.D. Geiger, Published by EDP Sciences, 2014
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Electricity is expected to remain the fastest growing form of worldwide end-use energy through 2030, as it has been for several decades. Gas turbines have been considered energy workhorses and are at the heart of almost all of the world’s electricity generating systems. Gas turbines are also used extensively for aircraft propulsion and other industrial applications. A gas turbine, also called a combustion turbine, is a type of combustion engine with a complex operating mechanism, and is known to operate in harsh environments that include extremely high temperature and pressure levels. The design of the modern gas turbine requires interdisciplinary knowledge of aerodynamics, thermodynamics, heat transfer, mechanical systems, material science and manufacturing technology. In addition, a designer of turbine engines must balance the conflicting requirements of heat transfer against those of aerodynamics, materials, stress, manufacturability and costs. In general they are subjected to significant thermo-mechanical stresses that affect the durability and reliability of its components and, in turn, the turbine itself. Achieving high reliability and thermal efficiency of gas turbines is of continuing concern and motivates engineers and researchers to study and improve turbine efficiency and turbine reliability. Increased thermal efficiency and power output require that turbines operate at high inlet temperatures. However, the increase in operating temperature requires high level of cooling system design, specifically blade internal cooling system design.
In this paper a new evolutionary numerical simulation approach for multiobjective design optimization is proposed and studied. To overcome the drawback of subjectively selecting weights to transform the multiple objective design problems into a single objective problem. A two design performance objectives and a set of design decision variables that influence the performance objectives are studied. This proposed approach automatically generates the most appropriate blade cooling channel design specifications that simultaneously optimize the two design objectives.
1.1 The working principle of gas turbines
The simplest and most common gas turbine is an in-line axial flow turbine, as shown in Figure 1. A gas turbine operates by guiding incoming air into the compressor, which in turn, compresses and delivers highly-pressurized air into the combustor section of the engine. This is the mainstream air flow. The combustor burns the injected fuel using the compressed air delivered from the compressor. The mainstream air flow (referred to as hot gas) is a combustion mix of air, fuel and unburned hydrocarbons, and it can reach temperatures as high as 1700 °C and can produce high pressure variations [1, 2]. The hot gas enters a series of turbine stages, where a stage is composed of a set of vanes and a set of blades. The hot gas expands towards atmospheric (or ambient) pressure in each stage, and this gas expansion runs the turbine to generate output shaft power. This shaft power is used to drive the compressor, and it is also used to power the generator. In case of aircraft gas turbine the shaft power runs propeller to generate thrust and exhaust is diverted to nozzle to generate secondary thrust required to propel aircraft.
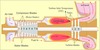 |
Figure 1. Cutaway view of typical industrial gas turbine engine (obtained from Britannica Encyclopedia, 1999). |
1.2 The gas turbine cooling system
The turbine engine parameter of greatest influence on core power and thermal efficiency is the turbine inlet temperature (TIT). To meet the demand requirements of power plants, such as increased thermal efficiency and increased power output, the owners of the gas turbines operate them at high inlet temperatures. During the last 30 years, the turbine inlet temperature for gas turbines has steadily increased (1200 °C–1700 °C) in order to improve thermal efficiency of the turbine. On the other hand, the allowable material temperature for the gas turbine hot gas path components has increased on a much slower rate. The historic increase in TIT, as shown in Figure 2, is a result of an attempt by gas turbine manufacturers to simultaneously increase the thermal efficiency and the specific core power per unit mass of air flow. The ideal Brayton Cycle curve, which is the performance theoretically obtainable with ideal components throughout the gas turbine engine, indicates a steady increase in specific core power until the Hydrocarbon Stoichiometric Limit is reached, which is the maximum temperature limit attained by burning fuel 100%. All existing gas turbine engine systems fall below this ideal curve. However, they follow the same general trend as this curve, from the very first gas turbine engines designed by Von Ohain (1939) and Whittle (1937) to more recent developments. Over this time span, there has been a several-fold increase in efficiency. However, there have also been very large increases in turbine inlet temperature.
 |
Figure 2. Historical trend of improving the core performance by increasing turbine rotor inlet temperature (Koff 1991; Reprinted with permission of the AIAA) |
One of the critical turbine components of hot gas path in gas turbine is the set of first-stage blades mounted on the rotor in the turbine section, as shown in Figure 1 and in Section 4 of Figure 3. Turbine blades, in general, are subjected to high centrifugal forces due to their rotary motion and are vulnerable to high instances of failure compared to other turbine components in the hot gas path. Increasing the TIT is the primary contributor to creating the harsh operating environment for these critical components. In addition, as the TIT increases, the heat transferred to the turbine blade material also increases the probability of blade failure due to thermal stresses, load on the blades and ceramic thermal barrier coating that protects the blades.
 |
Figure 3. Sectional view of an industrial power plant gas turbine (Courtesy of Siemens). |
In an effort to achieve the high levels of blade durability, the effective cooling of gas turbine components has received increasing attention in recent years. This has caused the rapid development of various methods to protect the gas turbine components. One such method is to cool these components using the highly-pressurized, compressed air of the mainstream flow that is diverted prior to the combustor section of the engine [3–5]. In essence, the turbine components in the hot gas path are cooled by a fraction of the compressed air (i.e., a secondary air flow) that is extracted by a cooling supply system from the compressor section of the engine (indicated by the dotted arrows in Figure 4). This secondary air flow of relatively cold and compressed air is called coolant, or cooling air. It is important to note that this extraction can reduce the thermal efficiency and power output of the turbine engine.
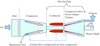 |
Figure 4. Schematic drawing of a gas turbine cooling supply system. |
Figure 5 shows cooling techniques commonly used for first-stage turbine blades with three major internal cooling zones – the leading edge (Zone 1), pressure and suction surfaces (Zone 2), and the blade tip region (Zone 3). The leading edge is cooled by both jet impingement and film cooling. The middle portion of the blade is cooled by serpentine rib-roughened internal cooling passages. The rib-roughened internal cooling passages cause turbulence in the coolant as the coolant passes over and around the ribs (or turbulators). The turbulent air removes a fraction of the heat conducted in Zone 2 from the blade (see Figure 5). The cooling air exits through the cooling holes in Zones 1, 2 and 3 forming a thin, cool, insulating blanket along the external surface of the turbine blade. The cooling effectiveness (ϕ) of these turbine blade cooling techniques depends on two parameters – the mass flow rate (ṁ) and the flow velocity (u) of the coolant. These two parameters greatly depend on the rib configuration in the serpentine internal cooling passages.
The mass flow rate ṁ of the coolant is usually measured as a percentage of the mainstream flow. Figure 6 shows that cooling effectiveness increases rapidly with a small percentage of coolant, but then the growth of the cooling effectiveness slows. To increase further cooling, a large amount of cooling air and/or different cooling techniques must be used. Since the cooling air is extracted from the compressor section of the engine, it represents a direct loss of engine efficiency due to a reduced amount of mainstream flow [2]. Figure 6 also shows that improvement in blade design can significantly increase the cooling effectiveness of the coolant at the same percentage of coolant flow. Despite the recent developments in internal cooling system technology, it is difficult to cool the blades significantly beyond an average cooling effectiveness of 0.50 (as shown in Figure 6). Thus, there is a need to explore further cooling passage configurations that directly impact a blade’s cooling effectiveness.
 |
Figure 6. Cooling effectiveness of different blade cooling design vs. cooling air flow (Moustapha et al. [2]). |
This research investigation focuses on optimizing the design configuration of the internal cooling passage of a turbine blade in order to enhance the cooling so that the desired cooling effectiveness is achieved. In general, the relationship among most of the critical components and internal subsystems in gas turbines are complicated, and the performance objectives of the turbine engine sometimes conflict. For example, the efficiency of gas turbines increases as TIT increases. However, operating at high temperatures decreases the life of the gas turbine engine and increases its operating costs. These conflicting objectives necessitate turbine blade design decisions that must consider trade-offs between the objectives. The optimization of the design configuration of the blade internal cooling passage gives rise to a multiobjective design optimization problem, where the two conflicting objectives are to: (1) maximize the cooling effectiveness, represented by the surrogate term heat transfer coefficient (h), to increase the blade life and reliability of the engine, and (2) minimize the pressure drop (Δp) in the cooling passage. The minimization of the pressure drop is important in that, enough pressure must be retained in the cooling passage for satisfactory ejection of the coolant flow. If there is insufficient pressure in the cooling air flow, the exit velocity of the coolant will be lower than that of the mainstream flow, and it will disturb the mainstream air flow. This disturbance is called mixing loss and can contribute to the loss of engine efficiency. Thus, minimization of pressure drop inside the cooling passage is an important objective for designers to consider.
2 Previous related literature
Over the last 50 years, there is a wide array of existing research concerning gas turbine blade cooling techniques. Researchers use analytical, computational and experimental methods to improve cooling techniques for gas turbine. Recent monographs focusing entirely on the gas turbine heat transfer and associated cooling technology is provided by Han et al. [3, 4] and Goldstein [6]. The use of multiobjective optimization in heat transfer problems is a relatively new area of focus and has been the point of interest only in recent years. In particular, the last few years have seen a sharp increase of heat transfer related optimization using evolutionary algorithms (EAs). Gosselin et al. [7] review multiobjective optimization using genetic algorithms, the more popular representative of the family of EAs, in heat transfer problems.
One of the well-known methods to improve the heat transfer (i.e., enhance material cooling) in a flow passage is to roughen the surfaces with turbulators (called ribs) in the blade’s internal cooling passages so that the surface area increases and enhances cooling. Gas turbine researchers study different design configurations of ribs in blade internal cooling passages to enhance the cooling process [8]. However, the use of rib turbulators poses other risks such as a decrease in coolant air flow pressure and a decrease in the velocity of coolant flow. Thus, a design optimization process capable of addressing multiple design objectives simultaneously can be a suitable tool in such conditions. The application of multiobjective design optimization to internal cooling passages not only helps enhance the blade cooling, but it can eventually be used in other areas such as heat exchanger/heat sink design, where cooling passages need to be optimized.
The optimization of cooling passage is extensively studied by Kim and Kim [9], who consider the optimization of internal cooling passages with straight rectangular ribs [10], V-shaped ribs [11] and the angle of the ribs [13]. They identify the values of geometric design variables with the objective function defined as a linear function of heat transfer coefficient and friction drag coefficient (pressure drop). They suggest that using a numerical approach presents a reliable way of designing optimized heat transfer surfaces. It is important to note that the two objectives considered in their study are heat transfer coefficient and pressure drop. However, these two objectives are combined to form a composite function using a vector of weights. The selection of the weights is based on designer’s experience, which could lead to errors in optimization if the factors are not carefully selected.
In summary, due to the complex nature of the flow and heat transfer phenomena involved in cooling passage design, only few attempts have been made in applying multiobjective optimization techniques to the design of turbine blade cooling passages. The limited studies consider two objective functions and convert the two objectives to a single composite objective function. However, no existing research simultaneously considers two objectives independently to optimize the design. The present work investigates a multiobjective design optimization method integrating evolutionary algorithms and numerical simulation to find a set of Pareto optima for the rib design in the internal cooling passage of the blade.
3 Proposed multiobjective design optimization framework
The overall goal of this research is to investigate and propose an approach that optimizes the gas turbine blade internal cooling channel design to enhance turbulent convective heat transfer while considering multiple design objectives simultaneously. The specific objectives of this research are to: (1) design a multiobjective procedure for the heat transfer optimization problem; (2) integrate a commercially-available simulation package used to build computational fluid dynamics (CFD) models for the analysis of the flow field and associated heat transfer of different design configurations of gas turbine blade cooling channels; and (3) automate the design optimization framework. Further the specific tasks aim of this research is to automate the process of finding the rib design for the cooling passage of a gas turbine blade that simultaneously maximizes the cooling effectiveness (i.e., the heat transfer coefficient h) increasing the blade life and reliability of the engine, and minimizes the pressure drop Δp increasing the engine efficiency. Due to symmetric nature of cooling passage and also to minimize the computational effort, only a periodic segment of cooling passage is selected in this study. Furthermore, this segment is simplified to a two-dimensional geometry with ribs on the bottom and top walls, as shown in Figure 7. It is the position and the shape of these ribs along the two walls that are to be optimized. The shape of the ribs depends on critical design variables. The radii (R 1 and R 2) of ribs 1 and 2 (in the periodic segment), and fillet radii (R 3, R 4, R 5 and R 6) between ribs and wall surface are considered as critical design variables that influence the values of objectives. Ribs induce separation and reattachment of flow to enhance the heat transfer by creating turbulent mixing. The heat transfer is greater at the reattachment locations, but it is low at the locations where flow separation takes place due to ribs. The flow separation and reattachment phenomenon is influenced by radii of the ribs.
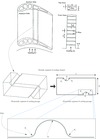 |
Figure 7. Selection of 2D periodic segment of the gas turbine blade cooling passage and design variables. |
The increase in radii R 1 and R 2 increases size of the ribs, surface area and turbulent mixing inside the cooling channel to enhance the heat transfer from blade to cooling air flow. However, an increase in rib size increases the drop in air flow pressure. Fillet radii decreases pressure drop and at the same time increases heat transfer rate by creating smooth surface contact between ribs and blade wall (refer to Figure 7 for an enlarged view of cooling channel ribs and fillets). Therefore, variations in these specifications can change the heat transfer coefficient h, and the pressure drop Δp.
The proposed optimization conceptual framework for gas turbine blade internal cooling passage design optimization is illustrated in Figure 8. In general, the framework is comprised mainly of an optimizer component and an evaluation component. The optimizer component iteratively generates multiple candidate rib configuration designs. Evaluation of the candidate designs are performed using numerical simulation, and the simulation can be viewed as a black box with: (1) an input interface that accepts and translates new design specifications and (2) an output interface that communicates objective function values to the optimizer component. The simulation component in this research uses computational fluid dynamics (CFD) numerical simulation. Based on the candidate design evaluation results, the optimizer utilizes these results to generate the next set of candidate designs through the perturbation of the evaluated designs. This cycle continues until the termination criteria are met. The next sections provide more details of the main design optimization procedure components therein.
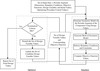 |
Figure 8. Overview of the proposed framework for mechanical component multiobjective design optimization. |
3.1 Solution evaluation component
For the specific design problem under study, the solution evaluation component or simulator evaluates the objective function values, heat transfer coefficient h and pressure drop Δp for a set of candidate design variable values generated by optimizer. In the present study, the radii (R 1 and R 2) of ribs 1 and 2, and fillet radii (R 3, R 4, R 5 and R 6) between ribs and wall surface are considered as critical design variables (refer to Figure 7). To obtain the objective function values for a given rib configuration, the coolant flow and heat transfer problem is solved for the periodic segment by numerical simulation. To solve the turbulent flow and heat transfer problem and to obtain the values for the objective functions, four main steps are performed: (1) generate computational model of 2D periodic segment of cooling channel using design variable values, (2) generate the mesh, (3) enforce the initial and boundary conditions for the geometric model and (4) solve flow and heat transfer governing equations. Figure 9 shows a pictorial view of process involved while solving a computational model for objective functions.
 |
Figure 9. Pictorial overview of the steps involved in solving computational model for objective function values. |
3.2 Optimizer component
Evolutionary Algorithms (EAs) are appropriate choice for solving multiobjective optimization problems. The dramatic increase in computational power and at the same time decrease in computational cost showing upward trend of using EAs to solve multiobjective optimization problems [12]. EAs are population-based optimization algorithms capable of finding multiple solutions in its final population that optimizes each objective simultaneously. Briefly, an EA-based optimization process starts with a randomly-generated initial population of size N individual solutions. The representation of the individual solution is given by binary strings, where each string is the binary representation of design variable values. Each set of binary strings in the population of individuals is evaluated using the simulator to find the corresponding fitness value (i.e., objective function value). A new population of individuals is created using three genetic operators: reproduction, crossover and mutation. The new population of individuals is then passed to the Simulation component for evaluation. This procedure continues to cycle until a termination criterion is met (in this study, a maximum number of iterations, called generations). The elitist Non-Dominated Sorting Genetic Algorithm II (NSGA II) proposed by Deb et al. [14], is currently one of the most popular EAs used to solve complex and real-world multiobjective optimization problems. Some of the salient features of NSGA II are its fast elitist sorting method that involves a combined pool of both the parent and child populations and provides diverse population using an autonomous crowding distance method. NSGA II introduces elitism by comparing the current population of candidate solutions with the previously found best nondominated solutions. In NSGA II, the selection procedure uses two processes: (1) Nondominated ranking and (2) crowding distance assignment. Figure 10 shows process flowchart for NSGA II for better understanding of the crowding distance and nondomination rank assignment process. A more detailed description about evolutionary algorithms and NSGA II can be found in Deb et al. [14, 15].
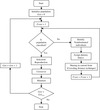 |
Figure 10. A flowchart of the working logic of NSGA II. |
3.2.1 Reproduction (or selection) operator
The primary objective of the reproduction operator is to copy the better performing candidate solutions and discard the poor performing solutions in the population, while maintaining the population size. This is achieved by performing the following tasks:
-
Identify the better performing solutions in a population based on their fitness values.
-
Make multiple copies of the better performing solutions to create the mating pool.
-
Discard poor performing solutions from the population so that the copies of the better performing solutions can be placed in the population.
3.2.2 The crossover operator
A crossover operator, also referred to as the recombination operator, is applied next to the candidate solutions of the mating pool. The crossover operator exchanges information between selected solution pairs (called parent solutions) with a probability of occurrence c. The simulated binary crossover (referred to in the literature as SBX) operator introduced by Deb and Agarwal [16] is performed in this algorithm.
3.2.3 The mutation operator
The crossover operator is primarily responsible for the intensification of the search and the mutation operator allows for diversification of the search to prevent the search process from becoming trapped at a local optimum. After crossover, the newly-generated solutions undergo a mutation operation, where operator changes a 1 to 0, and vice versa, with a mutation probability of occurrence m. The polynomial mutation operator introduced by Deb and Goyal [17] is employed by NSGA II in which the probability distribution is polynomial.
4 Optimization and results
In this research, the four steps of solution evaluation are performed using numerical Multiphysics modeling and simulation software COMSOL. In addition, the Non-dominated Sorting Genetic Algorithm II (NSGA II) proposed by Deb et al. [14] is used as the optimizer component. However, the impetus and success of this research investigation is not necessarily predicated upon using these specific approaches.
4.1 Design variables and input parameters
Recall that six design variables R 1 and R 2 (radii of Ribs 1 and 2, respectively) and fillet radii R 3, R 4, R 5, and R 6 are considered in this research investigation. Thus, results show only 2D rib shapes based on the radii of the ribs and fillet radii of the ribs in the cooling channel. Various parameters and variables are used in both the COMSOL numerical simulation and NSGA II. The parameters and range of initial values of the variables are now summarized. In COMSOL, the computational domain is selected and defined (Figure 11). The value ranges of the design variables R 1 through R 6 are given in Table 1. These ranges are approximated based on experimental results by Han et al. [3]. Next, Flow Physics is used to reflect the realistic conditions of internal cooling passage flow to correctly simulate the characteristics of the fluid flow. Here, compressed air (coolant) with non-isothermal and turbulent flow physics is used. Table 2 shows the material properties (density, dynamic viscosity) of air at atmospheric temperature and pressure, and these properties are imposed through the Graphical User Interface (GUI) of COMSOL. For simplicity the inlet boundary conditions are assumed to be constant boundary conditions. This study did not considered the effect on the inlet boundary conditions due to the change in ribs configuration at each simulation.
 |
Figure 11. Cooling channel with design variables R 1, R 2, R 3, R 4, R 5, and R 6. |
Design variables and value ranges (meters).
Initial subdomain conditions used for the COMSOL numerical simulation.
Table 3 summarizes initial boundary conditions used to solve objective functions in the COMSOL simulation environment. The cooling channel Inlet Flow (Condition 1) is subjected to a temperature (T) and velocity (u) to create necessary turbulence in the flow. Conditions 2 and 3 are wall boundaries, where fluid velocity is zero, and it is maintained at constant temperature, larger than that of the coolant. At the Outlet Flow Condition 4 indicating fluid departure, typically a relative pressure and convective heat flux is imposed. The boundary conditions are used as initial conditions to solve the governing equations iteratively to predict approximate fluid flow and heat transfer properties inside the cooling passage.
Initial boundary conditions used for the CFD simulation.
A pilot study has been conducted to determine the effect of evolutionary algorithms control parameters on different problems. Table 4 lists suggested MOEA control parameters used in this research investigation. The population size, N, is the number of candidate design solutions at each generation. A small population size can limit the capability of exploration of the search space and inhibits the purpose of crossover operations. Conversely, use of large population size can be computationally-expensive. For this study, a population size of N = 50 is used. The maximum number of generations, Gen max, denotes the number of generations (i.e., iterations) when to terminate the MOEA and to report the best set of design solutions so far. From the pilot study it is observed that convergence of solutions to optimal front at Gen max = 100 generations. In EAs, the creation of new solution is carried out by crossover operator. The crossover probability, c, defines how often crossover is performed. A low crossover probability decreases the speed of convergence due to lower exploration rate. On the other hand, a high probability may contribute to premature convergence. In general, the recommended range of c is between 0.60 and 0.95. Likewise, the mutation probability, m, denotes how often parts of an individual solution undergoes random perturbations. It introduces diversity into the population and should be a small value to avoid the algorithm from becoming a random search. In general, the recommended range of m is between 0 and 0.20. From the pilot study c = 0.90 (or, 90%) and m = 0.10 (or, 10%) shown better convergence rate.
NSGA-II input control parameters.
4.2 Discussion of the results
The heat transfer coefficient h is computed and summed along the top and bottom walls of periodic segment of the cooling passage using the boundary integration method. Pressure drop ∆p is obtained by computing the difference between inlet and outlet air flow pressures using the boundary integration method. The optimization framework is executed for population size N = 50 and maximum generations Gen max = 100 generations.
4.2.1 Single objective functions optimization
The goal in single objective optimization is to converge to the (global) optimum. Single-objective problems either minimize or maximize the objective function value depending upon the problem type attempting to reach single optimum value. In cooling channel design optimization, the heat transfer coefficient (h) is selected as an objective function because of its importance in blade cooling. The objective here is to maximize the value of h varying design variable values. The results of optimization of h for 2, 4 and 6 design variables are presented below.
Figure 12a shows graphical representation of single-objective optimization results for two design variables. The y-axis represents objective function, heat transfer coefficient (h), which needs to be maximized, whereas the x-axis represents number of generations (Gen max). The objective function (h) value at each generation is average of 50 objective function values (Pop) in that generation and it is compared with highest value of h in the same generation (Figure 12a). It is observed that the convergence of objective function h to global optimal value is linear and rapidly converge within the first few generations (five generations). In other words, the convergence rate slows and remains almost constant after 5th generation. To save computational time, one could stop the optimization process just after the 5th generation and report results. The best value of h found in this case is 15.4253 W/m2 K (over an average of 50 design specifications in the population). Similarly, the initial h value is 13.3949 W/m2 K (over an average of 50 design specifications in the population). As a result, a 15.15% increase in heat transfer coefficient or cooling effectiveness (directly proportional to HTC) is achieved.
 |
Figure 12. Convergence behavior of single objective to the (global) optimum. |
Next from Figure 12b, it is evident that the convergence rate in the case of four design variables is slow and appears to take more generations than the two design variable problem. The average global optimal value of h found in this case is 16.2793 W/m2 K (over an average of 50 design specifications in the population). Similarly, the average initial h value is 13.7239 W/m2 K (over an average of 50 design specifications in the population). A 18.62% increase in the heat transfer coefficient is achieved. By introducing the fillet radii as design variables, the four design variable problem resulted in 5.53% more cooling effectiveness than two design variable problem.
Similarly from Figure 12c, again it is evident that the convergence rate in case of six design variables further slows down compared to both the four and two design variable problem. The average global optimal value of h found in this case is 17.8476 W/m2 K (over an average of 50 design specifications in the population). Similarly, the average initial h value is 13.9687 W/m2 K (over an average of 50 design specifications in the population). An average a 27.75% increase in heat transfer coefficient is achieved. By introducing the additional fillet radii as design variables, the six design variable problem results in 15.70% more cooling effectiveness than the two design variable problem and 9.63% more cooling effectiveness than the four design variable problem.
4.2.2 Multiple (two) objective optimization
In the single-objective optimization problem, it is seen that the solution converges to one solution. Therefore, one can easily chose the final design specifications to use without ambiguity. But, when more than one objective functions are considered simultaneously for optimization and a Pareto-based optimization approach as proposed in this research, there exists a number of trade-off, or compromise, solutions. Without any further information, no solution from the set of compromise solutions can be said to be better than any other in the set. Thus, in multiobjective optimization, an effort must be made in finding the set of trade-off optimal solutions by considering all objectives to be equally important. Thus, it can be conjectured that there are two goals in a multiobjective optimization. First, set of solutions that is as close to the Pareto-optimal front as possible must be identified. Second, the set of solutions must be as diverse as possible. After a set of such trade-off solutions are found, a user can then use higher-level preference information to make a choice. The above such trade-off solutions are obtained a multiobjective optimization involves two search spaces instead of one. In single-objective optimization, there is only one search space – the decision variable space. However, in multiobjective optimization, there exists an associated space called objective, or criteria, space. Section below presents results of cooling channel design considering two objectives – heat transfer coefficient (h) and coolant pressure drop (Δp).
Figure 13 shows Pareto optimal frontier for two objectives with two, four, and six design variables in Figures 13a, 13b, and 13c, respectively. For example, Figure 13a shows the initial solution (Gen max = 0 generation) and the efficient frontier after 100 generations (Gen max = 100). The x-axis represents pressure drop ∆p, which is to be minimized. The y-axis represents heat transfer coefficient h, which is to be maximized. Note that the heat transfer coefficient objective function value is multiplied by −1 to convert it to an objective for minimization by the duality principle. After 100 generations, the solutions converge to the true Pareto optimal front with diverse set of solutions. The Pareto optimal front for the two objectives four design variables (Figure 13b) and two objectives six design variables (Figure 13c) suggest that the solutions are not converging to a smooth and uniform Pareto frontier as shown in the two-variable case. This is because the solution space of the problem increases exponentially with the increase in the number of decision variables. Therefore, more search iterations (i.e., generations) with an efficient search strategy (i.e., fine-tuning the search control parameters such as crossover c and mutation m) is required to explore more promising regions.
 |
Figure 13. Pareto optimal frontier for two objectives at the initial generation and at Gen max = 100 generations. |
The interpretation of the turbine blade cooling passage designs along the Pareto front can be seen in Figure 14, which is the set of Pareto optima at N = 50 and Gen max = 100. Figure 14 highlights three of the 50 design solutions along the Pareto frontier. Each of the three highlighted design solutions is shown with its corresponding temperature distribution color plot image of the periodic segment of the blade internal cooling passage. At the entrance (the left side boundary) of each plot, an inlet temperature of the coolant is applied. The top and bottom wall surfaces are maintained at a constant temperature. From the color plot, it can be concluded that the temperature of the incoming cool air (dark blue) increases because it is picking up heat from the surfaces (i.e., top and bottom) because of the turbulence caused by the ribs while flowing through the cooling passage. In Figure 14, it can be seen that tradeoff Solution 1 (Design 1) has smaller rib radii seen in the temperature distribution color plot image. The values of the radii R 1 and R 2 design variables are given in the inside table (for illustration purpose two main design variables rib radii R 1 and R 2 selected here). Solution 1 has minimal pressure drop (Δp = 0.1485 N/m2) and a low heat transfer coefficient (h = 11.09 W/m2 K). The temperature distribution color plot image for tradeoff Solution 3 (Design 3) shows larger ribs with a high pressure drop (Δp = 0.5783 N/m2) and a high heat transfer coefficient (h = 15.42 W/m2 K). The tradeoff Solution 2 (Design 2) shows a combination of large and small ribs with moderate pressure drop (Δp = 0.295 N/m2) and heat transfer coefficient (h = 13.82 W/m2 K).
 |
Figure 14. Specifications of gas turbine blade internal cooling channel ribs for three selected design solutions after 100 generations. |
5 Summary and future work
The main objective of this research is to propose a multiobjective design optimization for mechanical component design, specifically gas turbine blade internal cooling passages. The proposed optimization framework is built by integrating multiobjective evolutionary algorithms and computational fluid dynamics numerical simulation. In this study, the MOEA NSGA-II and the multiphysics numerical simulation software COMSOL is used. The results from the proposed multiobjective design optimization show the promise of the proposed approach to be used for the automated optimization of the rib designs inside a 2D cooling channel of a gas turbine blade. Even further, this research shows the promise of the proposed simulation multiobjective optimization approach to any mechanical component design optimization process.
The proposed approach is demonstrated for a 2D geometry with up to six design variables and two objectives considered. The next steps of this research effort include an enhancement on the work described in this paper. First, a third, relevant and very practical objective will be considered – the minimization of the material consumption in cooling passage design and blade manufacturing. Material consumption is a surrogate for material cost. Second, additional design variables that allow for more complex rib design geometries will be introduced. Finally, an intelligent approach to cluster Pareto optimal solutions can aid a decision-maker in reducing the design options thereby reducing the time to identify the best design option that satisfies the designer preferences.
References
- Boyce MP. 2006. Gas Turbine Engineering Handbook, 3rd edn. Gulf Professional Publications: Boston. [Google Scholar]
- Moustapha H, Zelesky MF, Baines NC, Japikse D. 2003. Axial and radial turbines. Concepts ETI Inc. [Google Scholar]
- Han JC, Dutta S, Ekkad S. 2001. Gas turbine heat transfer and cooling technology, 1st edn. Taylor & Francis: New York. [Google Scholar]
- Han JC. 2004. Recent studies in turbine blade cooling. International Journal of Rotating Machinery, 10(6), 443–457. [Google Scholar]
- Logan E. 2003. Handbook of Turbo Machinery, 2nd edn. CRC Press: New York. [CrossRef] [Google Scholar]
- Goldstein RJ. 2001. Heat Transfer in Gas Turbine Systems. Annals of the New York Academy of Sciences: New York. [Google Scholar]
- Gosselin L, Maxime G, François MP. 2009. Review of utilization of genetic algorithms in heat transfer problems. International Journal of Heat and Mass Transfer, 52, 2169–2188. [CrossRef] [Google Scholar]
- Ligrani PM, Oliveira MM, Blaskovich T. 2003. Comparison of heat transfer augmentation techniques. AIAA Journal, 41, 337–362. [CrossRef] [Google Scholar]
- Kim KY, Kim HM. 2002. Shape optimization of rib-roughened surface to enhance turbulent heat transfer. International Journal of Heat & Mass Transfer, 45, 2719–2727. [CrossRef] [Google Scholar]
- Kim HM, Kim KY. 2004. Design optimization of rib-roughened channel to enhance turbulent heat transfer. International Journal of Heat and Mass Transfer, 47, 5159–5168. [CrossRef] [Google Scholar]
- Kim KY, Lee YM. 2007. Design optimization of internal cooling passage with V-shaped ribs. Numerical Heat Transfer: Part A: Applications, 51, 1103–1118. [CrossRef] [Google Scholar]
- Deb K. 2007. Current trends in evolutionary multiobjective optimization. International Journal for Simulation and Multidisciplinary Design Optimization, 1(1), 1–8. [CrossRef] [EDP Sciences] [Google Scholar]
- Kim KY, Kim HM. 2004. Optimization of the three-dimensional angled ribs with RANS analysis of turbulent heat transfer. Proceedings from the ASME Turbo Expo: Vienna, Austria. [Google Scholar]
- Deb K, Agrawal, S, Pratap, A, Meyarivan, T. 2002. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II, IEEE Transactions on Evolutionary Computation, 6(2), 182–197. [Google Scholar]
- Deb K. 2001. Multi-Objective Optimization using Evolutionary Algorithms, 1st edn. John Wiley & Sons: New York. [Google Scholar]
- Deb K, Agarwal, RB. 1995. Simulated binary crossover for continuous search space. Complex System, 9, 115–148. [Google Scholar]
- Deb K, Goyal M. 1996. A combined genetic adaptive search (GeneAS) for engineering design. Computer Science and Informatics, 26(4), 30–45. [Google Scholar]
Cite this article as: Nagaiah NR & Geiger CD: Evolutionary numerical simulation approach for design optimization of gas turbine blade cooling channels. Int. J. Simul. Multisci. Des. Optim., 2014, 5, A22.
All Tables
All Figures
 |
Figure 1. Cutaway view of typical industrial gas turbine engine (obtained from Britannica Encyclopedia, 1999). |
| In the text | |
 |
Figure 2. Historical trend of improving the core performance by increasing turbine rotor inlet temperature (Koff 1991; Reprinted with permission of the AIAA) |
| In the text | |
 |
Figure 3. Sectional view of an industrial power plant gas turbine (Courtesy of Siemens). |
| In the text | |
 |
Figure 4. Schematic drawing of a gas turbine cooling supply system. |
| In the text | |
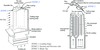 |
Figure 5. The schematic of a modern gas turbine blade with common cooling techniques [4]. |
| In the text | |
 |
Figure 6. Cooling effectiveness of different blade cooling design vs. cooling air flow (Moustapha et al. [2]). |
| In the text | |
 |
Figure 7. Selection of 2D periodic segment of the gas turbine blade cooling passage and design variables. |
| In the text | |
 |
Figure 8. Overview of the proposed framework for mechanical component multiobjective design optimization. |
| In the text | |
 |
Figure 9. Pictorial overview of the steps involved in solving computational model for objective function values. |
| In the text | |
 |
Figure 10. A flowchart of the working logic of NSGA II. |
| In the text | |
 |
Figure 11. Cooling channel with design variables R 1, R 2, R 3, R 4, R 5, and R 6. |
| In the text | |
 |
Figure 12. Convergence behavior of single objective to the (global) optimum. |
| In the text | |
 |
Figure 13. Pareto optimal frontier for two objectives at the initial generation and at Gen max = 100 generations. |
| In the text | |
 |
Figure 14. Specifications of gas turbine blade internal cooling channel ribs for three selected design solutions after 100 generations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




