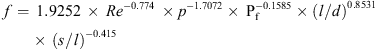| 期号 |
Int. J. Simul. Multidisci. Des. Optim.
卷号 8, 2017
|
|
|---|---|---|
| 文献编号 | A3 | |
| 页数 | 8 | |
| DOI | https://doi.org/10.1051/smdo/2016011 | |
| 网上发表时间 | 2017年1月23日 | |
Research Article
Performing multiobjective optimization on perforated plate matrix heat exchanger surfaces using genetic algorithm
Department of Mechanical Engineering, College of Engineering Trivandrum, Thiruvananthapuram, Kerala
695 016, India
* e-mail: anishkjohn@gmail.com
Received:
18
March
2016
Accepted:
15
November
2016
Matrix Heat Exchanger is having wide spread applications in cryogenics and aerospace, where high effectiveness and compactness is essential. This can be achieved by providing high thermal conductive plates and low thermal conductive spacers alternately. These perforated plate matrix heat exchangers have near to 100% efficiency due to low longitudinal heat transfer. The heat transfer and flow friction characteristics of a perforated plate matrix heat exchanger can be represented using Colburn factor and friction factor. In this paper, dimensionless parameters like Reynolds number (Re), porosity (p), perforation perimeter factor (P f), plate thickness to pore diameter ratio (l/d) and spacer thickness to plate thickness ratio (s/l) have been optimized for maximum Colburn factor and minimum friction factor using genetic algorithm. Two algorithms, one for single objective and the other for multi-objective problems, which are believed to be more efficient, are described. The algorithms coded with MATLAB, is used to perform multi-objective optimization on perforated plate matrix heat exchanger surfaces. The results show promising results.
Key words: Matrix Heat Exchanger / Colburn factor / friction factor / Optimization / Genetic Algorithm / Perforated plate
© A.K. John and K. Krishnakumar, published by EDP Sciences, 2017
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Introduction
The need for small size and light weight heat exchanger in all varieties of powered vehicles from automobiles to space crafts, as well as in a multitude of applications has resulted in the development of many heat transfer surfaces that are much more compact than can be practically realized with circular tubes. Heat exchangers are among the most vital components of any cryogenic refrigeration/liquefaction system and for these applications, heat exchangers should possess very high effectiveness. Determining the basic heat transfer and flow friction characteristics of heat transfer surfaces will help to understand the basic mechanisms involved for the development of matrix heat exchanger. Rationally optimized heat exchanger design, the development of new surfaces of superior characteristics and the development of methods of fabrications of compact surfaces for high temperature services can be obtained after the experimental analysis of different compact heat exchanger surfaces. The performance of refrigerators, liquefiers and separation units is strongly dependent on the effectiveness of the heat exchangers used. If the effectiveness of the heat exchanger is below a certain critical value (<85%) [1] most cryogenic processes would cease to function. A decrease in heat exchanger effectiveness from 97% to 95% reduces the liquefaction by 12% [2]. The low values of attainable coefficient of performance (COP) [3] and the resulting high cost of refrigeration make it economically sensible to use a more effective and expensive heat transfer equipment. Apart from having a high effectiveness, cryogenic heat exchangers also need to be very compact, i.e. they must accommodate a large amount of surface area in a small volume. This helps in controlling heat exchange with the surroundings by reducing exposed surface area. Besides, a small mass means a smaller cooling load and a faster cooling time for refrigerators. This requirement is particularly important for small refrigerators operating at very low temperature. The requirement to attain high effectiveness and high degree of compactness together in one unit led to the invention of matrix heat exchangers [4].
The performance of matrix heat exchangers (MHE) can be analyzed using Colburn factor (j) and friction factor (f). Heat transfer data for MHE is presented in the form of Colburn factor (j) vs. Reynolds number (Re) and flow friction data in the form of friction factor (f) vs. Reynolds number (Re).
Perforated plate matrix heat exchangers (MHE) essentially consist of a stack of perforated plates made of high thermal conductivity material alternating with spacers made of low thermal conductivity material. The stack of alternate high and low thermal conductivity materials is bonded to form a monolithic block. A schematic diagram of perforated plate MHE is shown as Figure 1. The gaps in between the plates ensure uniform flow distribution (by continuous reheadering) and create turbulence which enhances heat transfer. Small perforations (diameter ranging from 1.5 mm to <0.4 mm) are made into the plates so that a large heat transfer coefficient and high surface area density (up to 6000 m2/m3) is achieved. The ratio of the plate thickness (length of the hole in the plate) to the diameter of the hole is on the order of 0.75, therefore, the thermal and hydrodynamic boundary layers do not become fully developed within the perforations, which results in high heat transfer coefficients and correspondingly high friction factors [5]. The flow within the small holes in the perforated plate is generally laminar. Due to their small hydraulic diameter and the low density of gases, the surfaces are usually operated in the Reynolds number range 500 < Re < 1500 [6]. The spacers, being of low thermal conductivity material, also help in reducing axial conduction and consequent deterioration of performance. The spacers perform multiple roles such as reducing the longitudinal heat conduction through the walls, reducing the flow maldistribution by reheadering the flow in each spacer, interrupting the boundary layer and thus enhancing the heat transfer coefficients.
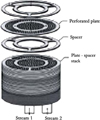 |
Figure 1. Perforated plate matrix heat exchanger. |
Literature review
Ozkol and Komurgov [7] optimized the design of the best-fitting heat exchanger in energy-converting systems using a genetic algorithm. In order to obtain the optimum heat exchanger, the geometry, the Number of Heat Transfer Units (NTU), and the pressure drop (dP) are considered to be the requirements to be satisfied. Gut and Pinto presented an optimization method for configuration selection for heat exchangers [8, 9]. Vargas and Bejan optimized heat exchangers using entropy-generation techniques [10, 11]. Most of these studies focus mainly on the physics of the fluid flow, and a complete analysis including dimensions of the body and cost is rare. Xie et al. [6] shows successful application of a genetic algorithm for thermal design and optimization of fin-and-tube heat exchangers. A generalized procedure has been developed to carry out the design and an optimization to find the minimum weight or annual cost of the heat exchangers, respectively, based on the Log-Mean Temperature Difference (LMTD) and the genetic algorithm technique. Genetic Algorithms (GAs) in thermal engineering are now generally using for solving real-world problems [12]. Prediction of the fin-tube heat exchanger performance [13], optimization of plate-fin heat exchangers [7, 14, 15], optimization of the geometry of cross-wavy and cross-corrugated primary surface recuperators [16, 17] are standing examples for strong ability of GA’s search and combined optimization. Correlations obtained from experimental data, were used to estimate the performance of compact heat exchanger using GAs [18, 19]. Multiobjective optimization algorithms are employed by Cavazzuti and Corticelli [20] to the maximization of the heat transfer and the minimization of the pressure drop for Re = 1000 and Pr = 0.74. Collaborative design software can be used in conjunction with computational fluid dynamics (CFD) in order to find optimum surfaces for compact heat exchangers. Hilbert et al. [13] optimize the shape of the blade in a tube-bank heat exchanger using a multi-objective genetic algorithm. Foli et al. [21] employ multiobjective evolutionary algorithms together with CFD simulations in order to optimize the shape of the separator between the hot and the cold stream in a micro heat exchanger. Nobile et al. [22] perform a multiobjective shape optimization of two dimensional periodic wavy channels using genetic algorithm. A similar work is presented by Manzan et al. [23]. Certainly, the optimized heat exchanger design can not only reduce the capital and running cost, but also achieve the purpose of energy savings. However, the traditional method is time consuming, and does not guarantee an optimal solution. Many researchers, reviewed in [24], applied the Genetic Algorithm (GA) [25] for designing the heat exchanger. The results outperformed the traditional method.
Methodology
The single blow transient test experiments [26] were carried out in an open circuit wind tunnel particularly designed for measuring the heat transfer and flow friction characteristics of different perforated plate matrix heat exchanger surfaces. A varying input was provided at the inlet section and the exit temperature response curve was obtained. The maximum slope of this curve was calculated and the corresponding time at the maximum slope was noted. Based on the maximum slope and time at which maximum slope occurs method, the NTU values were obtained. The exit temperature response is used for the experimental determination of NTU and longitudinal heat conduction factor, λ. The corresponding Colburn factor (j) was calculated from NTU and the basic performance data for a perforated plate matrix heat exchanger surface are often shown as curves of the Colburn factor (j = St Pr2/3) and the Fanning friction factor (f), plotted vs. Reynolds number (Re).
The effects of porosity, shape, pore diameter, thickness of plate and spacer thickness were examined using the experiments. The correlations for j and f are obtained by regression analysis in terms of dimensionless parameters like Reynolds number (Re), porosity (p), perforation perimeter factor (P f), plate thickness to pore diameter ratio (l/d) and spacer thickness to plate thickness ratio (s/l).
The correlations are as follows:
The objective functions in the proposed model of optimization are based on these correlations. For optimization of perforated plate matrix heat exchanger, the design variables are Reynolds number (Re), porosity (p), perforation perimeter factor (P f), plate thickness to pore diameter ratio (l/d) and spacer thickness to plate thickness ratio (s/l) so that j should be maximized and f should be minimized. The aim is to develop a fast and efficient multi-objective optimization technique by using GA (Genetic Algorithm) method, in order to solve multi-objective optimization problems with constraints. Also a hybrid approach is also suggested and studied. MATLAB shall be used to code the algorithm.
Genetic algorithm
Genetic algorithms are a part of evolutionary computing, which is a rapidly growing area of artificial intelligence. Idea of evolutionary computing was introduced in the 1960s by I. Rechenberg in his work “Evolution strategies” [27]. Genetic Algorithms (GAs) were invented by John Holland and published in a book “Adaption in Natural and Artificial Systems” in 1975 [28]. In 1992 John Koza has used genetic algorithm to LISP evolve programs to perform certain tasks and called his method “genetic programming” (GP) (Figure 2) [29].
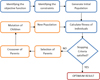 |
Figure 2. Flow chart showing the steps involved in genetic algorithm. |
A Genetic Algorithm (GA) is a search technique that mimics the process of natural selection. This heuristic search technique is routinely used to generate useful solutions to optimization and search problems. Genetic algorithms belong to the larger class of evolutionary algorithms (EA), which generate solutions to optimization problems using techniques inspired by natural evolution, such as inheritance, mutation, selection, and crossover. Algorithm is started with a set of solutions called population. Solutions from one population are taken and used to form a new population. Solutions which are selected to form new solutions (offspring) are selected according to their fitness – the more suitable they are the more chances they have to reproduce. This is repeated until some condition (number of populations or improvement of the best solution) is satisfied.
The steps involved in genetic algorithm are as follows:
-
Start Generate random population of n chromosomes (suitable solutions for the problem)
-
Fitness Evaluate the fitness f(x) of each chromosome x in the population
-
New population Create a new population by repeating next steps until the new population is complete
-
Selection Select two parent chromosomes from a population according to their fitness
-
Crossover With a crossover probability cross over the parents to form a new offspring (children)
-
Mutation With a mutation probability mutate new offspring at each locus
-
Accepting Place new offspring in a new population
-
-
Replace Use new generated population for a further run of algorithm
-
Test If the end condition is satisfied, stop, and return the best solution in current population
-
Loop Go to step 2.
Objective functions and constraints
The objective function for j is
The generalization for function provided in genetic algorithm is for minimization of a problem. Therefore, another function g(x) should be provided such that g(x) = −f(x) to make the objective function for the maximization problem.
The constraints are chosen in this problem so that the optimized value will be inclusive in the experimentation values. The single blow transient test experiments are conducted in the laminar region where the characteristic dimension is pore diameter. Perforation perimeter factor is the ratio of perimeter length of the perforation to the plate thickness. All the constraints provided for both j and f are linear bounds.
The objective function for f is
The solution of this problem will give two optimum conditions: one which is having maximum j and other which is having minimum f value. The exact solution we required is one optimum condition which satisfies both objective functions. Therefore we are performing a multi-objective optimization using genetic algorithm. A hybrid scheme is used to find an optimal Pareto front for multiobjective problem.
Genetic operators
Each population of randomly selected solution of the problem is represented as genes in genetic algorithm. Joining genes create a binary bit string of values, denoting each member of population called chromosome. A chromosome evolves through iterations, called generation. A fitness or objective function is required, after representation. A selection of parents for reproduction and recombination for creating offspring is essential during the run. These aspects are called GA operators. A selection or reproduction operator during reproduction phase of GA selects parents from population which they create offspring by recombination comprising next generation. The main objective of selection operator is to keep and duplicate the fit solutions and eliminate the poor chromosomes, while keeping the size of population constant and some schemes are tournament selection, proportionate selection, ranking selection, Roulette Wheel Selection (RWS) and Stochastic Universal Selection (SUS). This operator cannot create new chromosomes to the initial population, it only make copies of good solutions. In reproduction phase, the two parents nominated by selection operator recombine to create one or more offspring with crossover or mutation operators. The main concept of different crossover operators is selecting two strings of solution (chromosomes) from the mating pool of selection operator and exchanging some portion of these two strings from randomly selected points. Single point cross over is one basic type of this operator for binary GA. A mutation operator is applied to individual solutions after cross over operator which a gene is randomly changed in a string with a small probability to create a new chromosome. This operator maintain the diversity of the population and increase the possibility of not losing any potential solution and find the global optimal, while cross over operator is a technique of rapid exploration of search space. The selection operator selects and maintains the good solutions; while crossover recombines the fit solutions to create a fitter offspring and mutation operator randomly alter a gene or genes in a string to hopefully find a better string.
Solution using genetic algorithm
MATLAB Optimization Toolbox 6.3 is used for optimization of perforated plate matrix heat exchanger surfaces to obtain maximum j and minimum f. Multi-objective genetic algorithm function “gamultiobj” in Global Optimization Toolbox can be used to solve multi-objective optimization problem in several variables. The multiobjective genetic algorithm (gamultiobj) uses a set of operators that are applied to the population set (points in the design space) which is under consideration. The initial population is generated randomly by default. The next generation of the population is computed using the non-dominated rank and a distance measure of the individuals in the current generation. A non-dominated rank is assigned to each individual using the relative fitness. One individual dominates another and have low non-dominated rank, if it is better in at least one objective and not worse in all objectives. The distance measure of an individual is used to compare individuals with equal rank by measuring the distance from other individuals with the same rank. The default distance measure function, DistanceMeasureFcn (function that computes distance measure of individuals) with option of @distancecrowding, is used to calculate the distance measure of an individual in this work.
The multiobjective GA function gamultiobj uses a controlled elitist genetic algorithm. An elitist GA always favors individuals with better fitness value (rank) whereas, a controlled elitist GA also favors individuals that can help increase the diversity of the population even if they have a lower fitness value. It is very important to maintain the diversity of population for convergence to an optimal Pareto front. An optimal Pareto front for our multiobjective problem is found by a hybrid scheme. Gamultiobj can reach the region near an optimal Pareto front relatively quickly, but it can take many function evaluations to achieve convergence. General technique used to get near an optimum front is to run gamultiobj for a small number of generations. Then the solution from gamultiobj is used as an initial point for fgoalattain, hybrid optimization solver that is faster and more efficient for a local search. Fgoalattain solves the goal attainment problem, which is formulation for minimizing a multiobjective optimization problem. The hybrid functionality in multiobjective function gamultiobj, the hybrid solver will start at all the points on the Pareto front returned by gamultiobj. But in single objective GA, the hybrid function starts at the best point returned by GA. The new individuals returned by the hybrid solver are combined with the existing population and a new Pareto front is obtained. Gamultiobj estimates the pseudo weights (required input for fgoalattain) for each point on the Pareto front and runs the hybrid solver starting from each point on the pareto front.
Results and discussion
Single objective optimization is applied on both objective functions (maximize j and minimize f) independently using genetic algorithm. The genetic algorithm uses constraint dependent mutation, stochastic uniform selection, heuristic crossover and forward migration. The single objective optimization maximizes j when the parameters Re = 50, p = 0.2, P f = 25, l/d = 0.6 and s/l = 0.5 and minimize f at Re = 1200, p = 0.4, P f = 25, l/d = 0.2 and s/l = 2 (Figure 3).
 |
Figure 3. Effect of population on an objective function. |
The best population size for optimization sets on 22 as j value maximizes at 0.145102. Best fitness plot for both j and f are plotted. The minimum value for f obtained is 0.00434364 (Figures 4 and 5).
 |
Figure 4. Best fitness plot on single objective optimization for j. |
 |
Figure 5. Best fitness plot on single objective optimization for f. |
There is no single solution to a multiobjective optimization problem. From single objective optimization, an optimal solution is obtained for each objective function. The goal of the multiobjective genetic optimization using genetic algorithm is to find a set of solutions in a range that lies between the optimal solutions of single objective optimization. The set of solutions with a good spread is known as Pareto front. All solutions on the Pareto front are optimal. The Pareto front is shown in the plots 6–8. The population size is 100. The multi objective genetic algorithm uses tournament selection with size of 4, constraint dependent mutation and heuristic crossover.
If the Pareto fronts obtained by gamultiobj alone and that obtained by using the gamultiobj with hybrid function are close, we can compare them using the spread and the average distance measures. The average distance of the solutions on the Pareto front can be improved by using a hybrid function called fgoalattain. The spread is a measure of the change in two fronts and that can be higher when hybrid function is used. This indicates that the front has changed considerably from that obtained by gamultiobj with no hybrid function.
Using the hybrid function will result in an optimal Pareto front but we may lose the diversity of the solution because fgoalattain does not try to preserve the diversity. This can be indicated by a higher value of the average distance measure and the spread of the front. We can further improve the average distance measure of the solutions and the spread of the Pareto front by running gamultiobj again with the final population returned in the last run without the hybrid function (Figures 6–8).
 |
Figure 6. Pareto front plot obtained from gamultiobj function alone. |
 |
Figure 7. Pareto front plot obtained from gamultiobj function and hybrid approach. |
 |
Figure 8. Optimal Pareto front. |
Conclusion
From the paper, the following conclusions are arrived.
-
Dimensionless parameters like Reynolds number, porosity, perforation perimeter factor, plate thickness to pore diameter ratio and spacer thickness to plate thickness ratio have been optimized for maximum Colburn factor and minimum friction factor using genetic algorithm.
-
Single objective genetic algorithm optimization shows maximum design value obtained for j is 0.145101 when the parameters Re = 50, p = 0.2, P f = 25, l/d = 0.6 and s/l = 0.5.
-
Single objective genetic algorithm optimization shows minimum design value obtained for f is 0.00434 when the parameters Re = 1200, p = 0.4, P f = 25, l/d = 0.2 and s/l = 2.
-
Multi objective genetic algorithm optimization plots the Pareto front without hybrid approach and with hybrid approach are found to be close.
-
Optimal Pareto front is obtained for multiobjective optimization using genetic algorithm.
References
- Barron R. 1985. Cryogenic Systems. Oxford University Press. [Google Scholar]
- Atrey MD. 1998. Thermodynamic analysis of Collins helium liquefaction cycle. Cryogenics, 38, 1199–1206. [CrossRef] [Google Scholar]
- Moon WJ, Lee PY, Jin YW, Hong ES, Chang MH. 2007. Cryogenic Refrigeration Cycle for Re-Liquefaction of LNG Boil-Off Gas, in Cryocoolers 14, International Cryocooler Conference Proceedings, Boulder. [Google Scholar]
- McMahon H, Bowen R, Bleyle GJr. 1950. A perforated plate heat exchanger. Trans ASME, 72, 623–632. [Google Scholar]
- Webb RL. 1987. Enhancement of Single-phase Heat Transfer. Kakac S, Shah RK, Bergles AE, Editors. Wiley: New York. [Google Scholar]
- Xie G, Wang Q, Sunden B. 2008. Application of a genetic algorithm for thermal design of fin-and-tube heat exchangers. Heat Transfer Engineering, 29(7), 597–607. [CrossRef] [Google Scholar]
- Ozkol I, Komurgoz G. 2005. Determination of the optimum geometry of the heat exchanger body via a genetic algorithm. Numerical Heat Transfer, Part A, 48, 283–296. [CrossRef] [Google Scholar]
- Amon CH, Mikic BB. 1991. Spectral element simulations of unsteady forced convective heat transfer: application to compact heat exchanger geometries. Numerical Heat Transfer, 19(1), 1–19. [CrossRef] [Google Scholar]
- Gut JAW, Pinto JM. 2004. Optimal configuration design for plate heat exchangers. International Journal of Heat and Mass Transfer, 47, 4833–4848. [CrossRef] [Google Scholar]
- Vargas JVC, Bejan A. 2001. Thermodynamic optimization of finned crossflow heat exchangers for aircraft environmental control systems. International Journal of Heat and Fluid Flow, 22, 657–665. [CrossRef] [Google Scholar]
- Bejan A. 2001. Thermodynamic optimization of geometry in engineering flow systems. Exergy An International Journal, 4, 269–277. [CrossRef] [Google Scholar]
- Sen M, Yang KT. 2000. Applications of artificial neural networks and genetic algorithms in thermal engineering, in The CRC Handbook of Thermal Engineering. Kreith F, Editor. CRC Press: Boca Raton, FL. p. 620–661. [Google Scholar]
- Hilbert R, Janiga G, Baron R, Thévenin D. 2006. Multi-objective shape optimization of a heat exchanger using parallel genetic algorithms. International Journal of Heat and Mass Transfer, 49, 2567–2577. [CrossRef] [Google Scholar]
- Pacheco-Vega A, Sen M, Yang KT, McClain RL. 1998. Genetic Algorithms-based Predictions of Fin-Tube Heat Exchanger Performance. Proceedings of 11th International Heat Transfer Conference, August 23–28, Kyongju, Korea, Vol. 6, pp. 137–142. [Google Scholar]
- Xie GN, Wang QW. 2006. Geometrical optimization of plate-fin heat exchanger using genetic algorithms. Proceedings of the Chinese Society for Electrical Engineering, 26(7), 53–57 (in Chinese). [Google Scholar]
- Mishra M, Das PK, Sarangi S. 2004. Optimum design of crossflow plate-fin heat exchangers through genetic algorithm. International Journal of Heat Exchangers, 5(2), 379–401. [Google Scholar]
- Liang HX, Xie GN, Zeng M, Wang QW, Feng ZP. 2005. Application Genetic Algorithm to Optimization Recuperator in Micro-Turbine The 2nd International Symposium on Thermal Science and Engineering, October 23–25, Beijing, China. [Google Scholar]
- Wang QW, Liang HX, Xie GN, Zeng M, Luo LQ, Feng ZP. 2007. Genetic algorithm optimization for primary surfaces recuperator of microturbine. ASME Journal of Engineering for Gas Turbines and Power, 129, 436–442. [CrossRef] [Google Scholar]
- Pacheco-Vega A, Sen M, Yang KT, McClain RL. 2001. Correlations of fin-tube heat exchanger performance data using genetic algorithms simulated annealing and interval methods. Proceedings of ASME the Heat Transfer Division, November 11–16, New York, USA, vol. 369–5, p. 143–151. [Google Scholar]
- Cavazzuti M, Corticelli MA. 2008. Optimization of heat exchanger enhanced surfaces through multiobjective genetic algorithms. Numerical Heat Transfer, Part A, 54, 603–624. [CrossRef] [Google Scholar]
- Foli K, Okabe T, Olhofer M, Jin Y, Sendhoff B. 2006. Optimization of micro heat exchanger: CFD, analytical approach and multi-objective evolutionary algorithms. International Journal of Heat and Mass Transfer, 49, 1090–1099. [CrossRef] [Google Scholar]
- Nobile E, Pinto F, Rizzetto G. 2006. Geometric parameterization and multi-objective shape optimization of convective periodic channels. Numerical Heat Transfer B, 50, 425–453. [CrossRef] [Google Scholar]
- Manzan M, Nobile E, Pieri S, Pinto F. 2008. Multi-objective optimization for problems involving convective heat transfer, in Optimization and Computational Fluid Dynamics, Chap. 8. Thévenin D, Janiga G, Editor. Springer-Verlag: Berlin. [Google Scholar]
- Gosselin L, Tye-Gingras M, Mathieu-Potvin F. 2009. Review of utilization of genetic algorithms in heat transfer problems. International Journal of Heat and Mass Transfer, 52, 2169–2188. [CrossRef] [Google Scholar]
- Goldberg DE. 1989. Genetic algorithms in search, optimization, and machine learning. Addison-Wesley Longman Publishing Co.: Boston, USA. [Google Scholar]
- Krishnakumar K, Venkatarathnam G. 2007. On the use of time at maximum slope in determining the heat transfer coefficients in complex surfaces using the single blow transient test method. International Journal of Heat Exchangers, VII, 31–44. [Google Scholar]
- Rechenberg I. 1965. Evolutionsstrategie: Optimierung Technischer Systeme nach Prinzipien der Biologischen Evolution. Frommann−Holzboog: Stuttgart. [Google Scholar]
- Holland JH. 1975. Adaptation in Natural and Artificial Systems, 2nd edition. University of Michigan Press. [Google Scholar]
- Koza JR. 1992. Genetic Programming: On the Programming of Computers by Means of Natural Selection. MIT Press. [Google Scholar]
Cite this article as: John AK & Krishnakumar K: Performing multiobjective optimization on perforated plate matrix heat exchanger surfaces using genetic algorithm. Int. J. Simul. Multisci. Des. Optim., 2017, 8, A3.
All Figures
 |
Figure 1. Perforated plate matrix heat exchanger. |
| In the text | |
 |
Figure 2. Flow chart showing the steps involved in genetic algorithm. |
| In the text | |
 |
Figure 3. Effect of population on an objective function. |
| In the text | |
 |
Figure 4. Best fitness plot on single objective optimization for j. |
| In the text | |
 |
Figure 5. Best fitness plot on single objective optimization for f. |
| In the text | |
 |
Figure 6. Pareto front plot obtained from gamultiobj function alone. |
| In the text | |
 |
Figure 7. Pareto front plot obtained from gamultiobj function and hybrid approach. |
| In the text | |
 |
Figure 8. Optimal Pareto front. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.