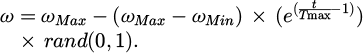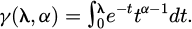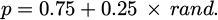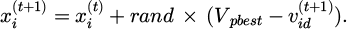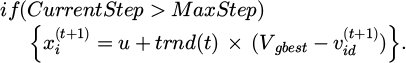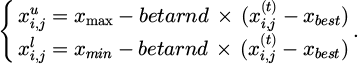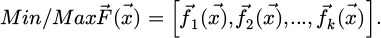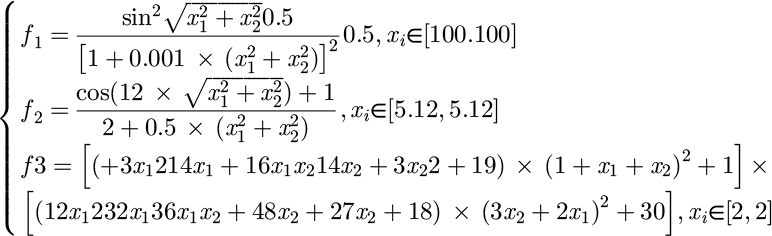| Issue |
Int. J. Simul. Multidisci. Des. Optim.
Volume 15, 2024
|
|
|---|---|---|
| Article Number | 3 | |
| Number of page(s) | 12 | |
| DOI | https://doi.org/10.1051/smdo/2024001 | |
| Published online | 15 March 2024 | |
Research article
Modeling and simulation of complex emergency dispatch based on BIPSO
School Computer and Communication Engineering, Nanjing Tech University Pujiang Institute, Nanjing, 210000, China
* e-mail: sunzm666@outlook.com
Received:
14
December
2023
Accepted:
8
February
2024
In emergency task scheduling, this study proposes a complex model for emergency scheduling. It is based on the particle swarm algorithm and improves upon the traditional version. Additionally, the study recommends the use of the binary particle swarm optimization algorithm (PSO). The study proposes applying the multi-objective task scheduling-particle swarm optimization algorithm (MOTS-PSO) to the complex emergency scheduling model by combining it with the multi-objective function. Compared to other algorithms, the proposed improved algorithm exhibited the lowest average number of iterations, which consistently fell within the range of 130, and achieved a 100% success rate for optimization searches on the majority of functions. When compared with other models, the proposed research model demonstrated superior performance, exhibiting the lowest total scheduling cost, total execution time, and data transfer time of 280 and 900, respectively, for the task quantity of 5000. Furthermore, the proposed model exhibited the lowest maximum execution cost for a single node, which remained within the range of 0.45S. The outcomes of the experiments demonstrate that the proposed research model adequately satisfies the requirements for complex scheduling and its simulability has been confirmed.
Key words: Particle swarm / optimization / contingency scheduling / scheduling cost / execution time
© Z. Sun and C. Huang, Published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
In contemporary society, the occurrence of emergencies and contingencies is on the rise, necessitating the implementation of corresponding emergency relief measures. In emergency situations, the efficient realization of task scheduling work is integral to emergency rescue efforts. As such, the successful completion of the contingency scheduling (CS) task is directly linked to the effectiveness of disaster rescue and reduction in loss. Most of the dispatching work has traditionally relied on human resources. But as society has advanced and developed, CS jobs have grown increasingly difficult and complex. This development has put forward higher requirements for CS personnel. Additionally, the face of increasingly diverse and complex emergencies and contingencies demands constant innovation and improvement of CS tasks. The application of modern information technology has increased the possibilities for CS tasks due to advances in science and technology [1,2]. Most current task scheduling employs particle algorithms, but they can suffer from issues such as a tendency to get trapped in local optimization during search for optimization [3–5]. The study enhances the conventional particle swarm optimization (PSO) and proposes a multi-objective scheduling approach to establish the model. MOTS-PSO model can achieve more accurate scheduling, reduce scheduling cost and realize scheduling tasks in complex emergency scheduling. The research is structured into four main parts. The first part summarizes PSO and task scheduling research by domestic and foreign scholars and analyzes the results. The second part constructs and analyzes the proposed model, introducing improvement methods for the model. The third section involves validating the effectiveness of the comparison experiments in relation to their actual application. The fourth section serves to summarize the experimental results, identify research limitations, and propose future directions for research.
2 Related works
The growing use of PSO is driving advances in medicine, the chemical industry, and other fields. This has sparked growth in a number of industries. An enhanced salp algorithm based on PSO was proposed by Dagal I and other academics to track the solar system's greatest power point. The study utilized photovoltaic solar panels with input voltages and currents that were monitored using PSO algorithm. The outcomes indicated that the efficiency of the proposed algorithm of the study reached 99.99%, 99.63% and 99.24% respectively when compared with other methods [6]. Zhang scholars proposed an assessment method incorporating PSO algorithm for rock bursts that can easily occur in mining. The study used impact pressure data to establish a BP regression model, while optimizing the connection weights in combination with the PSO algorithm. The outcomes indicated that the method proposed by the study, compared with the standard BP method to improve the accuracy by 15%, verifying that the method had accuracy and overall applicability [7]. Bi and other scholars proposed a PSO synthesized improvement method for PSO in response to problems such as low search efficiency. The method combined dynamic adaptive PSO with ecds-PSO algorithm, discarded the particle velocity, and simplified the overall second-order difference equation into a first-order difference equation. Results of experiments indicated that the proposed method improved the algorithm accuracy while enhancing the efficiency of the algorithm [8]. Liu and other scholars in the field of materials proposed a hybrid algorithm based on a two-population evolutionary strategy. The algorithm combined with PSO algorithm and used the information sharing mechanism to achieve co-evolution, which increased the diversity of individuals. The study's suggested method was shown to have the best resilience and optimization seeking abilities when compared to other algorithms, according to evaluation results [9]. Abadi MQ H and other scholars proposed the HSSAGA model to address the scheduling problem of medical personnel during the COVID-19 epidemic. This model utilized the Salp group algorithm to solve the scheduling and assignment problems of nurses. Experimental results demonstrated that the proposed algorithm outperforms the most advanced algorithm [10]. Dagal I et al. proposed the SSPSO algorithm for the independent battery charging system. This algorithm utilized a hybrid series salp particle optimization algorithm to achieve maximum power point tracking. Simulation results demonstrated that the proposed algorithm is highly efficient, with an average tracking efficiency of 99.99% [11]. Chalh et al. proposed a new method for MPPT based on Gull optimization algorithm to solve the problem of using the maximum power point tracking controller. The method utilized fewer operators and modified parameters. The performance of this method was compared to other methods in an 80W photovoltaic system, and the experimental results confirmed its effectiveness [12]. Ibrahim A L W and other scholars proposed an SSA-PSO method to solve problems with DC bus capacitors. The method used a hybrid salp group algorithm and PSO, along with an intelligent synovial controller, to eliminate instability in DC bus voltage. Simulation results demonstrated the method's effectiveness in output power extraction and current harmonic reduction [13].
In the realm of task scheduling, numerous scholars have researched using optimization algorithms, including deep learning and genetic algorithms [14–16]. Rigo and other scholars designed a task scheduling branch pricing algorithm for satellite scheduling tasks. The algorithm incorporated a dynamic programming algorithm to decompose the task and apply it to large-scale tasks in extended time. Comparing the proposed algorithm of the study with other algorithms, the algorithm was able to plan more complex tasks in an optimal manner within a reasonable time [17]. A recursive search artificial bee colony technique was proposed by Gao and other researchers to solve the scheduling optimization problem of concurrent testing activities. The study obtained a series of implied sequences during the search process, and searched for the scheduling plan with minimum completion time through the implied sequences. The study's suggested algorithm was able to accomplish the goal of creating efficient tests in the least amount of time, according to the trial findings, which were compared with other approaches [18]. For robotic work cells, Xidias and colleagues introduced a scheduling approach based on a genetic algorithm and an adaptive neuro-fuzzy system for motion planning and job scheduling issues. The method planned both collision-free motion and optimal path time, combining a geometric approach with an adaptive neuro-fuzzy system to configure the manipulator. Tests revealed that the suggested approach could identify the ideal manipulator setups and demand point sequences more quickly [19]. Natarajan and other scholars proposed a scheduling method based on ant colony algorithm (ACA) in the field of cloud computing. The method combined with load balancing and uses ACA technique for cloud load balancing task. Experiments were carried out to compare the research proposed method with alternative approaches. The findings of the experiments showed that the research proposed method reduced the execution time and operational cost while improving the efficacy of the ACA in cloud load balancing [20].
In summary, while some scholars have made progress in PSO and task scheduling research, there is currently insufficient research in the field of CS. The issue of premature convergence arises when implementing traditional particle swarm scheduling. This paper investigates the enhancement of the particle swarm algorithm. The paper innovatively improves the PSO algorithm for complex emergency scheduling, enhancing the algorithm's accuracy and better meeting scheduling requirements.
3 Complex CS modeling based on PSO
Facing the complex task CS, the study is based on PSO and improves it. Then combined with the multi-objective task function, the multi-task goal scheduling strategy is proposed to be applied to the complex CS model.
3.1 Particle swarm task scheduling algorithm
The deployment and implementation of tasks in complex situations require several technical supports, including the most important one is the task scheduling technique. Task scheduling is a combinatorial optimization problem, and the result of task scheduling is related to the efficiency of the whole task implementation, which has a very crucial role in the task processing in emergency situations [21]. Task scheduling is to establish an appropriate order of task implementation within a certain time frame according to the emergency of the task. The parameters of the model to achieve the best performance are selected. The principle of task scheduling is shown in Figure 1.
Figure 1 shows the schematic diagram of task scheduling. After the user submits the task, the big data network will analyze and process the task according to the execution time and specifics of the task, integrate the analysis results, and distribute the results to each user. Heuristic optimization techniques, such as genetic algorithms, ACAs, firefly algorithms, and PSO, have been employed a lot in recent years to tackle scheduling difficulties. PSO is selected for the study to solve scheduling problems in complex situations due to its advantages such as high efficiency and fast convergence, fewer parameters and easy implementation [22–24]. PSO has several advantages, including few algorithm parameters and simple implementation for processing scheduling tasks. Additionally, PSO has a good effect in dealing with discretization problems, which is important since most of the data in task scheduling schemes are discretized data information. Therefore, this paper has chosen PSO as a task scheduling strategy to study. The core idea of PSO can be summarized as follows: assume that there exists a search space with particle population size N and spatial dimension n dimensions, the n-dimensional vector of particle i velocity is denoted Vi = {vi1, vi2, ..., vin}, and the n dimensional position vector is denoted Xi = {xi1, xi2, ..., xin}. During the search process, the i th generation particle searches for two kinds of optimal position information, one is pbest, for the local optimal position searched by the particle within the population. The other is gbest, for the global optimal position searched by the particle in the whole particle population. Denoting the vector Pi = {Pi1, Pi2, ..., Pin} as the local optimal solution and the vector Gbesti = {Gbesti1, Gbesti2, ..., Gbestin} as the global optimal solution, the way of updating the velocity of the particle of the i th generation at the moment of t +1 is expressed as equation (1).
In equation (1), ω denotes the inertia weights during the iteration process, r1, r2 denotes two random numbers taking values between [0,1], and c1, c2 denotes the learning factor, which is the acceleration factor of the particle in flight. The way of updating the position of the particle in the ith generation at the moment of t +1 is expressed as equation (2).
The variation of the task scheduling scheme can be realized by using equation (2). After realizing the iterative process, the PSO records the global optimal position, which is the result of this task scheduling. During the task scheduling process, the position vector Xi = {xi1, xi2, ..., xin} of PSO is equivalent to the corresponding task scheduling scheme. The process of PSO is shown in Figure 2.
The PSO flowchart is displayed in Figure 2. The swarm's information exchange allows PSO to identify the best solution through the structure as illustrated, and during the iteration phase, all particles migrate to the global optimal particle position. Standard particle swarms are generally used in solving continuous problems such as function optimization, and three-stage coding is used for task scheduling, in which individuals are generated as shown in Figure 3.
Figure 3 shows the schematic diagram of individual generation. As shown in the figure, the individual generation approach is also divided into three parts; all individuals in the population follow a grouping strategy for learning, which updates the three codes of the individuals in turn.
 |
Fig. 1 Task scheduling schematic. |
 |
Fig. 2 Particle swarm algorithm flowchart. |
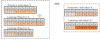 |
Fig. 3 Individual generation schematic. |
3.2 Optimization and improvement of CS strategies
PSO will have problems such as premature convergence, optimal solution traps and imbalance between local and global search when performing task scheduling, to address the above problems, the study proposes an improved PSO (BIPSO). BIPSO is improved from five aspects such as adaptive inertia weights, dynamic learning factors, flower pollination algorithm, firefly algorithm mixing, and boundary processing, and the impact effects of the improved approach are shown in Figure 4 Shown.
Figure 4 displays the impact of the five enhancements on the algorithm. The PSO's inertia weight ω influences the particles' search capability throughout the optimization process. When utilizing inertia weight ω >1, particle flight speed in multidimensional space increases gradually over time until maximum velocity is reached, resulting in a more dispersed particle population. Conversely, when employing inertia weight 0 < ω ≤ 1, particle flight speed decreases. A greater value of ω supports global exploration, while a lesser value of ω bolsters local exploitation ability. Initially, global space exploration necessitates a higher ω to increase species diversity, while later on, a lower ω is required for local search ability. The study employs a nonlinear decreasing function to enhance inertia weights, and the upgraded adaptive inertia weights are denoted as equation (3).
In equation (3), t denotes the iterations of the algorithm, T max denotes the maximum iterations of the algorithm, and ωMax = 0.9, ωMin = 0.4.
Changes to the adaptive weights can make the inertia weights shrink continuously through iterations. The learning factor reflects the information interaction between the populations, c1, c2 regulates the flight of particles towards the individual empirically optimal population and the global empirically optimal population, respectively. Typically, the learning factors c1, c2 change over time, and this change is realized using the gamma function, which is expressed as equation (4).
In equation (4), it is possible to make the learning factor c1 progressively smaller and the learning factor c2 progressively larger during the iteration process. The improvement scheme for the PSO learning factor is expressed as equation (5).
In equation (5), NumItr represents the maximum number of iterations, cmax = 2.5, cmin = 0.5, λ = 0.1. The flower pollination method is a heuristic swarm intelligence algorithm that includes two processes: self-pollination and heteroflower pollination. The processes of self-pollination and heteroflower pollination are comparable to the local and global search processes, respectively, and the probability p = 0.8 maintains a balance between both. The local optimal solution will eventually be reached by the traditional PSO since it does not handle global and local searches in a balanced manner. Therefore, the search mechanism is switched using the flower pollination algorithm, and the switching probability B is expressed as in equation (6).
Equation (6) can be used to balance the PSO's local and global searches, which increases PSO's convergence accuracy while also accelerating PSO's convergence and assisting particles in leaving the local optimal solution. At this point, the location of the improved global search is expressed as equation (7).
In equation (7), L(λ) represents the Levy flight function in the flower pollination algorithm, ε represents a random number in the range between 0 and 1, Vpbest represents the locally optimal velocity value in the particle search process, and Vgbest represents the globally optimal velocity value in the particle search process. PSO may fall into the local optimal state unable to jump out in the late iteration, at this time combined with the firefly algorithm for improvement. The two types of the new local search position update approach are as follows: in the first, the local search position update is expressed in equation (8) when the “elite solution” proves to be superior than the global optimal solution.
In equation (8), u denotes an “elite solution”, and rand denotes a random number whose values satisfy the standard normal state distribution. When the firefly technique is used, it can result in “storage” and assist particles in leaving the local optimal solution and reexamining it. Equation represents the local search position update when the “elite solution” is the cause of the current solution (9).
In equation (9), the local search position can be updated when the elite solution is weaker than the current solution. In the particle swarm iteration process, a detection value MaxStep is set to determine whether the number of iterations in which the PSO optimal solution does not change exceeds MaxStep. Equation (10) represents the method that assists the algorithm in breaking out of the local optimal solution.
In equation (10), trnd(t) denotes t distribution. If the number of iterations in which the PSO optimal solution does not change exceeds MaxStep, the particle is caught in a local optimal trap, and the position vector is initialized with the “optimal solution” stored by the firefly algorithm. Particle swarms often cross the boundary in flight, and the particle swarm boundary problem needs to be handled. The conventional processing method involves replacing the particle position value with the established boundary value when it exceeds the limit. However, it is not easy to discern the impact of particle optimization since the general boundary value lacks the characteristics of the ideal solution. The study adopts a suitable boundary variation method to process the particle positions, and the particle positions are re-initialized according to equation (11).
In equation (11), 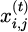 is the current position of the particle, xbest is the optimal value of the particle position during the iteration process, and betrand represents the beta distribution function. In task scheduling problems, multi-objective optimization problems are very common, and the multi-objective problem is defined as equation (12).
is the current position of the particle, xbest is the optimal value of the particle position during the iteration process, and betrand represents the beta distribution function. In task scheduling problems, multi-objective optimization problems are very common, and the multi-objective problem is defined as equation (12).
In equation (12), 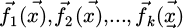 represents each objective function to be optimized and
represents each objective function to be optimized and  represents the vector of decision variables. Multiple objective functions must be considered while solving a multi-objective problem. In order to handle the multi-objective task scheduling problem in conjunction with the emergency scenario, a multi-objective task scheduling-particle swarm optimization algorithm (MOTS-PSO) is presented and used to the sophisticated computer science model. The task scheduling strategy flow is shown in Figure 5.
represents the vector of decision variables. Multiple objective functions must be considered while solving a multi-objective problem. In order to handle the multi-objective task scheduling problem in conjunction with the emergency scenario, a multi-objective task scheduling-particle swarm optimization algorithm (MOTS-PSO) is presented and used to the sophisticated computer science model. The task scheduling strategy flow is shown in Figure 5.
Figure 5 shows the MOTS-PSO process, where tasks are scheduled and processed based on the policy flow. For the validation of the algorithm and the model, nine basis functions are selected as in equations (13)–(15).
See equation (13) below
Equation (13) for three low-dimensional functions, where i=1,2, functions f1 and f2 obtain the global optimum min(f(x))= -1 at x={0,0}, and function f3 obtains the global optimum min(f(x)=3 at x ={0,1}. Functions f4, f5, and f6 are denoted as equation (14).
Equation (14) for three peak one-dimensional functions, where i=1,2,..n. Functions f4, f5, and f6 obtain the global optimum value min(f(x))=0 at x={0,0,..,0}. Functions f7, f8, and f9 are denoted as equation (15).
Equation (15) for three peak multidimensional functions, where i = 1,2,..n. Functions f7, f8, and f9 obtain the globally optimal value min(f(x)) = 0 at x = {0,0,..,0}.
 |
Fig. 4 Impact of changes in improvement methods on the algorithm. |
 |
Fig. 5 MOTS-PSO process. |
4 Performance study of complex CS models
The study investigates the performance of the proposed complex CS model by first experimentally comparing the optimization of the proposed BIPSO algorithm to verify its effectiveness. After that, the simulability of the strategies in the model is verified in different scenarios.
4.1 Analysis of improved PSO performance
The computer configuration used for the experiments was Windows 10 operating system, Intel Core i7-8750H processor, and 16G RAM, the deep learning framework version was Pytorch 1.10, and Python version was 3.7. In this configuration the standard PSO, linearly decreasing inertia weight PSO (LPSO) was selected to compare with the research proposed BIPSO. The parameters of the model to achieve the best performance are selected. Table 1 displays the parameter settings for every algorithm.
Table 1 displays the basic parameter settings for each of the three algorithms. Although the linearly declining mechanism of inertia weights introduced by LPSO improves global search capabilities in the late search, it also has drawbacks such as randomness and a shift in search efficiency with particle count. According to the above settings f1, f6 and f9 are selected as test functions, the MSError of the average convergence value is 0.02. The convergence effect of the average value is shown in Figure 6.
The average convergence outcomes of the three techniques for various functions are displayed in Figure 6. The convergence plot of the f1 function is displayed in Figure 6a, where it is evident that the BIPSO method converges considerably faster than both LPSO and PSO, leading to a convergence in the vicinity of −1 after 100 iterations. Figure 6b shows the convergence plot of the f6 function, where all three functions converge to lower values as the iterations increases, with BIPSO converging the fastest and showing the best convergence accuracy. Figure 6c shows the convergence plot of the f9 function, BIPSO stays at a lower value after convergence and finally converges to about 3, while PSO and LPSO converge to a higher value. f1 is a low-dimensional function, f6 is a high-dimensional single-peak function, and f9 is a high-dimensional multiple-peak function, so BIPSO outperforms LPSO and PSO in terms of convergence speed and accuracy in either low-dimensional or high-dimensional functions. And the convergence time of BIPSO is shorter. f1–f9 is selected as the test function, and f6 is a high-dimensional single-peak function, and f9 is a high-dimensional multiple-peak function. f1–f9 as test functions, the average convergence algebra of the three algorithms is shown in Figure 7.
The average convergence algebra results of various techniques on the functions under test are displayed in Figure 7. The figure shows that the BIPSO function has the lowest number of convergence generations among the different functions, while the LPSO and PSO functions have a higher number of convergence generations. In terms of low dimensional functions, the BIPSO convergence algebra takes only 30 generations, while the LPSO and PSO iterations take up to 242 generations each. The BIPSO function's convergence algebra remains within 20 generations in the high-dimensional single-peak function, while the LPSO iteration reaches up to 175 generations and the PSO iteration algebra reaches up to 200 generations. In the high-dimensional multi-peak function, the number of convergence generations of BIPSO increases with the complexity of the function and stays within 130 generations. The number of convergence generations of PSO and LPSO mostly stays around 300 generations, with the maximum PSO iterations reaching 452 generations and the maximum number of LPSO iterations reaching 315 generations. More generations indicate that the algorithm operates slower, and BIPSO has the fastest operation speed compared to PSO and LPSO. Figure 8 displays the optimization outcomes of the three techniques on the f1–f9 test function.
The optimization outcomes of several techniques on the test functions are displayed in Figure 8. From the figure, in the low-dimensional function, the success rate of BIPSO optimization is 100%, while the success rate of LPSO and PSO is much lower than that of BIPSO, and the success rate of LPSO optimization is higher than that of PSO. In the high-dimensional single-peak function, the success rate of BIPSO optimization is 86.35% on the f5 function, and the success rate of BIPSO optimization is 100% on the f4 and f6. BIPSO and PSO have the largest difference in optimization success rates, with PSO staying around 50% and LPSO staying around 70%. In the peak multidimensional function, BIPSO's merit search success rate decreases, but remains higher than LPSO and PSO, with the merit search success rate remaining above 66%. The PSO merit seeking success rate stays around 40%, while the LPSO merit seeking success rate stays around 50%. From the above experimental results, BIPSO outperforms PSO and LPSO in terms of convergence speed, convergence accuracy, and success rate of optimization search, which indicates that the improvements proposed by the study are effective. The convergence speed of the algorithm is improved by using adaptive inertia weights and dynamic learning factors. Additionally, the convergence accuracy is further enhanced by utilizing the flower pollination algorithm. Finally, the search efficiency is increased by incorporating the firefly algorithm, which helps to avoid getting trapped in local optima.
Parameter settings for each algorithm.
 |
Fig. 6 Mean convergence results of the three algorithms in different functions. |
 |
Fig. 7 Average convergence algebra results of different algorithms on test functions. |
 |
Fig. 8 Optimization results of different algorithms on test functions. |
4.2 Scheduling model performance analysis
In order to verify the effectiveness of the suggested MOTS-PSO scheduling approach, MOPSO is chosen to be compared with FA. The parameters of the model to achieve the best performance are selected. Table 2 displays the three algorithms' parameter configurations.
The three scheduling methods' parameter sets are displayed in Table 2. The Multi-objective PSO technique simulates the behavior of bird flocks in nature to solve multi-objective optimization problems and accomplish efficient search across many function spaces. The firstfly technique (FA) is a heuristic optimization technique that mimics the mutual attraction behavior of fireflies to find the ideal solution to a given problem. The study sets up two experimental scenarios to validate the experimental performance in various settings. Scenario 1 is a small-scale task scenario where 10 task sequences are added at a time and the number of scheduling is between 10 and 100. Scenario 2 is a large-scale task scenario in which 100 task sequences are added each time and the number of scheduling is from 1000 to 5000. The results of different scheduling algorithms in Scene 1 are shown in Figure 9.
Figure 9 shows the comparative results of different algorithms in terms of total scheduling cost, total execution and data transfer time, and maximum execution cost of a single node in small-scale tasks. From the figure, in small-scale task scenarios, the results of the research proposed MOTS-PSO are better than MOPSO with FA in several metrics. In the total cost of task scheduling, the total cost of MOTS-PSO scheduling stays around 6, while MOPSO with FA stays around 7 and MOTS-PSO has the least total cost. The total execution and data transmission time stays low as the tasks rises, hovering around 18 for MOTS-PSO and higher at roughly 20 for MOPSO & FA. In the comparison of maximum execution cost of single node, MOTS-PSO has lower values compared to the other two algorithms and basically stays around 0.25 s, while FA stays around 0.3 s and MOPSO stays around 0.35 s. Overall, in small-scale task execution, the proposed MOTS-PSO is optimal among the three scheduling schemes, with the least execution cost as well as the shortest execution time. In scenario 2, the results of different scheduling algorithms are shown in Figure 10.
Figure 10 shows a comparison of the effect of different algorithms in terms of total cost of scheduling, total execution and data transfer time, and maximum execution cost of a single node in large-scale tasks. When there are 1000 tasks, the differences between the algorithms are not as noticeable in terms of the overall cost of task scheduling; nonetheless, the total cost of scheduling various algorithms increases when the number of tasks increases significantly. When processing multiple tasks, there are limitations to consider, such as memory and processor capacity. For instance, when the MOTS-PSO algorithm processes a task sequence of 5000, the calculation time is 0.45 s. When the number of tasks is 5000, the total cost of MOTS-PSO scheduling is the least and stays around 280, while the total cost of FA scheduling stays around 340 and MOPSO stays around 360. In the total comparison of total execution time and total data transfer time, MOTS-PSO outperforms the other two algorithms, as the sequence of tasks increases from 1000 to 5000, the MOTS-PSO time consumption increases from 200 to around 900. Whereas FA increases from 200 to 1100, MOPSO time consumption is the most, increasing from 200 to 1200. In single node maximum execution cost, as the task sequence increases, the MOTS-PSO execution cost also increases from the initial 0.45 s and finally smoothes out to 0.45 s, while the FA execution cost increases from 0.42 s to 0.7 s, and the MOPSO execution cost increases from 0.55 s to 0.72 s. Thus, in large-scale task scheduling, the study proposes algorithms that outperform the other two algorithms.
Parameter settings for each algorithm.
 |
Fig. 9 Comparison of the effect of different algorithms on the total cost of scheduling, total execution and data transfer time, and the maximum execution cost of a single node in a small-scale task. |
 |
Fig. 10 Comparison of the effect of different algorithms on the total cost of scheduling, the total execution and data transfer time, and the maximum execution cost of a single node in large-scale tasks. |
5 Conclusion
The study proposed an emergency scheduling model based on particle swarm algorithm for scheduling problems in complex situations. The study introduced the Bounded Inertia Particle Swarm Algorithm which builds on the traditional PSO. The study presented a strategy for scheduling multiple tasks in emergency situations that involves addressing various objectives simultaneously. The study compared the performance of the BIPSO algorithm proposed herein against LPSO and traditional PSO algorithms. The BIPSO algorithm performed better than the other two algorithms across various dimensional functions, according to the results. On average, the BIPSO algorithm required the fewest iterations to converge within 130 generations. The BIPSO algorithm is a highly effective optimization method with a search success rate of 100% for more than half of the functions, surpassing the success rate of the other two algorithms for the remaining functions. In large-scale tasks, MOTS-PSO outperformed the other two algorithms in terms of total scheduling cost, total execution and data transfer time, and single-node maximum execution cost metrics, which were 280, 900, and 0.45 s respectively for a task number of 5000. The study findings suggested that the MOTS-PSO proposed is capable of meeting the demands of complex emergency scheduling, but also highlight certain limitations. The methodology optimized inertia weights and learning factors separately without assessing the potential synergies between the two parameters. The relationship between these two crucial characteristics can be explored in more research to increase the algorithm's accuracy even further.
Funding
The research is supported by Study on scheduling optimization of multi-level response for multi-region epidemic prevention and control in cloud environment (njpj2022-1-27).
Conflict of interest disclosure
The authors have no competing interests to declare that are relevant to the content of this article.
Authors contributions
Zimei Sun analyzed the data and Chengning Huang helped with the constructive discussion. Zimei Sun. and Chengning Huang made great contributions to manuscript preparation. All authors read and approved the final manuscript.
References
- J. Békési, G. Dósa, G. Galambos, A first fit type algorithm for the coupled task scheduling problem with unit execution time and two exact delays, Eur. J. Oper. Res. 297, 844–852 (2022) [CrossRef] [Google Scholar]
- H. Nishikawa, K. Shimada, I. Taniguchi, H. Tomiyama, Mouldable fork-join task scheduling techniques with inter and intra-task communications, Int. J. Embed. Syst. 15, 69–81 (2022) [CrossRef] [Google Scholar]
- Y.W. Ti, S.K. Chen, W.C. Wang, A hierarchical particle swarm optimisation algorithm for cloud computing environment, Int. J. Inf. Comput. Secur. 18, 12–26 (2022) [Google Scholar]
- Y.J. Chiu, B. Li, S.R. Jian, S.Y. Lien, J.M. Yi, Improved particle swarm optimization algorithm for photovoltaic system under local shading, J. Chin. Inst. Eng. 45, 632–643 (2022) [CrossRef] [Google Scholar]
- W. Zhang, Y. Ran, G. Zhang, Y. Shao, Optimal allocation of product reliability using novel multi-population particle swarm optimization algorithm, Proc. Inst. Mech. Eng., Part C: J. Mech. Eng. Sci. 236, 4565–4576 (2022) [CrossRef] [Google Scholar]
- I. Dagal, B. Akın, E. Akboy, Improved salp swarm algorithm based on particle swarm optimization for maximum power point tracking of optimal photovoltaic systems, Int. J. Energy Res. 46, 8742–8759 (2022) [CrossRef] [Google Scholar]
- M. Zhang, Prediction of rockburst hazard based on particle swarm algorithm and neural network, Neural Comput. Appl. 34, 2649–2659 (2022) [CrossRef] [Google Scholar]
- Y. Bi, A. Lam, H. Quan, C. Wang, A comprehensively improved particle swarm optimization algorithm to guarantee particle activity, Russ. Phys. J. 64, 866–875 (2021) [CrossRef] [Google Scholar]
- H. Liu, S. Duan, H. Luo, A hybrid engineering algorithm of the seeker algorithm and particle swarm optimization, Mater. Test. 64, 1051–1089 (2022) [CrossRef] [Google Scholar]
- M.Q.H. Abadi, S. Rahmati, A. Sharifi, M. Ahmadi, HSSAGA: designation and scheduling of nurses for taking care of COVID-19 patients using novel method of hybrid salp swarm algorithm and genetic algorithm, Appl. Soft Comput. 108, 107449 (2021) [CrossRef] [Google Scholar]
- I. Dagal, B. Akın, E. Akboy, A novel hybrid series salp particle Swarm optimization (SSPSO) for standalone battery charging applications, Ain Shams Eng. J. 13, 101747 (2022) [CrossRef] [Google Scholar]
- A. Chalh, R. Chaibi, A.E. Hammoumi, S. Motahhir, A.E. Ghzizal, M. Al-Dhaifallah, A novel MPPT design based on the seagull optimization algorithm for photovoltaic systems operating under partial shading, Sci. Rep. 12, 21804 (2022) [CrossRef] [Google Scholar]
- A.L.W. Ibrahim, F. Zhijian, H.M.H. Farh, I. Dagal, A.A. Al-Shamma'a, A.M. Al-Shaalan, Hybrid SSA-PSO based intelligent direct sliding-mode control for extracting maximum photovoltaic output power and regulating the DC-bus voltage, Int. J. Hydrog. Energy 51, 348–370 (2024) [CrossRef] [Google Scholar]
- Y. Guo, Z. Mustafaoglu, D. Koundal, Spam detection using bidirectional transformers and machine learning classifier algorithms, J. Comput. Cognit. Eng. 2, 5–9 (2022) [CrossRef] [Google Scholar]
- M.K. Marichelvam, M. Geetha, Solving industrial multiprocessor task scheduling problems using an improved monkey search algorithm, Int. J. Oper. Res. 41, 135–149 (2021) [CrossRef] [MathSciNet] [Google Scholar]
- J. Yu, M. Wang, Y. JH, S.M.S Arefzadeh, A new approach for task managing in the fog-based medical cyber-physical systems using a hybrid algorithm, Circuit World 49, 294–304 (2023) [CrossRef] [Google Scholar]
- C.A. Rigo, L.O. Seman, E. Camponogara, E. Morsch Filho, E.A. Bezerra, P. Munari, A branch-and-price algorithm for nanosatellite task scheduling to improve mission quality-of-service, Eur. J. Oper. Res. 303, 168–183 (2022) [CrossRef] [Google Scholar]
- J. Gao, X. Zhu, R. Zhang, Optimization of parallel test task scheduling with constraint satisfaction, J. Supercomput. 79, 7206–7227 (2023) [CrossRef] [Google Scholar]
- E. Xidias, V. Moulianitis, P. Azariadis, Optimal robot task scheduling based on adaptive neuro-fuzzy system and genetic algorithms, Int. J. Adv. Manuf. Technol. 115, 927–939 (2021) [CrossRef] [Google Scholar]
- Y. Natarajan, S. Kannan, G. Dhiman, Task scheduling in cloud using aco, Recent Adv. Comput. Sci. Commun. (Formerly: Recent Patents on Computer Science), 15, 348–353 (2022) [Google Scholar]
- T. Bezdan, M. Zivkovic, N. Bacanin, I. Strumberger, E. Tuba, M. Tuba, Multi-objective task scheduling in cloud computing environment by hybridized bat algorithm, J. Intell. Fuzzy Syst. 42, 411–423 (2022) [Google Scholar]
- L. Wang, P. Zheng, Y. Ji, X. Chen, Multi-objective optimization of a Stirling cooler using particle swarm optimization algorithm, Sci. Technol. Built Environ. 28, 379–390 (2022) [CrossRef] [Google Scholar]
- J. Zhang, Y. Yang, An optimisation of 3D printing parameters of nanocomposites based on improved particle swarm optimisation algorithm, Int. J. Microstruct. Mater. Prop. 16, 266–277 (2023) [Google Scholar]
- Y.W. Chen, Dynamic interception point guidance algorithm based on particle swarm optimization, Meas. Control. 55, 983–995 (2022) [CrossRef] [Google Scholar]
Cite this article as: Zimei Sun, Chengning Huang, Modeling and simulation of complex emergency dispatch based on BIPSO, Int. J. Simul. Multidisci. Des. Optim. 15, 3 (2024)
All Tables
All Figures
 |
Fig. 1 Task scheduling schematic. |
| In the text | |
 |
Fig. 2 Particle swarm algorithm flowchart. |
| In the text | |
 |
Fig. 3 Individual generation schematic. |
| In the text | |
 |
Fig. 4 Impact of changes in improvement methods on the algorithm. |
| In the text | |
 |
Fig. 5 MOTS-PSO process. |
| In the text | |
 |
Fig. 6 Mean convergence results of the three algorithms in different functions. |
| In the text | |
 |
Fig. 7 Average convergence algebra results of different algorithms on test functions. |
| In the text | |
 |
Fig. 8 Optimization results of different algorithms on test functions. |
| In the text | |
 |
Fig. 9 Comparison of the effect of different algorithms on the total cost of scheduling, total execution and data transfer time, and the maximum execution cost of a single node in a small-scale task. |
| In the text | |
 |
Fig. 10 Comparison of the effect of different algorithms on the total cost of scheduling, the total execution and data transfer time, and the maximum execution cost of a single node in large-scale tasks. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.