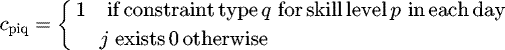| Issue |
Int. J. Simul. Multidisci. Des. Optim.
Volume 11, 2020
|
|
|---|---|---|
| Article Number | 10 | |
| Number of page(s) | 10 | |
| DOI | https://doi.org/10.1051/smdo/2020002 | |
| Published online | 24 July 2020 | |
Research Article
A tabu search approach with embedded nurse preferences for solving nurse rostering problem
1
Department of Decision Science, School of Quantitative Sciences, Universiti Utara Malaysia, 06010 Sintok, Kedah, Malaysia
2
Computer Science Department BINUS Graduate Program, Bina Nusantara University, Jakarta, 11480, Indonesia
* e-mail: syariza@uum.edu.my
Received:
20
October
2019
Accepted:
11
May
2020
This paper presents an intelligent tabu search (TS) approach for solving a complex real-world nurse rostering problem (NRP). Previous study has suggested that improvement on neighborhoods and smart intensification of a TS could produce faster and fitted solution. In order to enhance the TS, this paper introduces an improvement to the neighborhoods and explores on the neighborhoods exploitations of TS to solve the NRP. The methodology consists of two phases: initialization and neighborhood. The semi-random initialization is employed for finding a good initial solution during the initialization phase which avoids the violation of hard constraints, while the neighborhood phase is established for further improving the solution quality with a special representation and innovative neighborhood generations within TS algorithm. The aim is to move sample points towards a high-quality solution while avoiding local optima by utilising a calculated force value. It is observed that the enhancement strategy could improve the solution quality of the constructed roster. It is concluded that the TS with enhancements approach is able to assign effective and efficient shift duties for the NRP especially when related with real-world working regulations and nurses preferences.
Key words: Nurse rostering problem / heuristics / nurse preference / tabu search / initial solution / neighborhood generation
© R. Ramli et al., published by EDP Sciences, 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Personnel scheduling exists in various fields, such as, healthcare, transportation, education, and sports [1]. Nurse scheduling problem (NRP) is considered as this type of problem where it focuses on the allocation of nurses to execute nursing services per shift per day in certain duration of time subject to a set of constraints. The constraints are defined by working regulations and nurses preferences and are usually very hard to satisfy especially for the real-world large scale of NRPs. It is known that through an efficient scheduling activity, nursing services and hospital operations can lead to an effective working condition and contribute to a higher quality of services [2].
NRP belongs to combinatorial optimization problem, which is classified to be NP-hard [3]. In solving real cases, it is known that NRP is very difficult to solve due to its problem size, complexity and highly constrained task. It is possible that no feasible solutions to such NRP would exist because of the large number of constraints that the scheduling attempts to satisfy. For this reason, the constraints are divided into two; hard and soft. The hard constraint must always be adhered to produce feasible solution. On the other hand, the soft constraint may be violated but need to be satisfied as much as possible to be of good quality scheduling. Examples of hard constraint within NRP are mandatory workdays constraints, ordering constraints and night shift constraints. Meanwhile, individual nurse preferences and special requests from the nurses are considered as soft constraints.
A wide variety of methodologies and models have been recognized to deal with different problem circumstances within the NRPs during the years. These include mathematical programming [4,5], constraint programming [6], constraint satisfaction [7] and meta-heuristics such as tabu search [8], simulated annealing [9], genetic algorithm [10], bee algorithm [11], hyper-heuristic [12], particle swarm optimization [13], harmony search algorithm [14], variable neighborhood search [15] and also its hybridization [16]. Nevertheless, most of the recent works on the NRPs attempted on various meta-heuristics approaches due to the search procedures that can escape from local optima and solve the NRP instance in an acceptable time limit. For a recent review on population based approaches for physician scheduling see [17].
Among the meta-heuristic approaches which give the best feasible solution and has proven to be very efficient on a variety of problems is the Tabu Search (TS) [18,19]. The TS is a very efficient technique in dealing with various combinatorial problems, which can be adopted for single or multi-objective problems. It has been recognized successfully in solving many practical optimization problems [19,20]. [18] defined that the most important distinguishing property of the TS is as the exploitation of adaptive form of memory. These take the form of short-term memory strategies (i.e., tabu list and aspiration criteria) and long-term memory strategies (e.g., intensification and diversification). The TS is quite established because of its solution quality and its efficient algorithm [21]. Various cases that were explored, among others, consist of control mechanism for the tabu tenure of TS, objective function with the automatic control mechanism based on weight, and the enlargement of the search neighborhood [20].
In a previous study, [22] employed hybrid TS approach to NRP in Belgian hospitals. The TS associated with specific problem solving heuristics has shown to contribute better quality rosters. In another study, [21] effectively produced roster for a large hospital using variant of TS that oscillates between searching the feasible cover and improved the preference cost. Besides, the study incorporated different neighborhood, candidate lists and tabu list. The tabu lists used are called as short nurse tabu list and day-night tabu list that prevent cycle during the search. A large neighborhood related with chain moves is introduced to ensure that the search visit many local optima. [2] used a hyper-heuristic method incorporated with tabu search as high-level heuristics and a number of low-level heuristics that oppose each other based on the rules motivated by reinforcement learning principal for solving NRP. A tabu list of heuristics is introduced to avoid certain heuristics from being chosen at certain times during the search. Study by [16] optimized the initial solutions using a local search with a 2-opt neighborhood and a tabu search. Their method compared very favorably with a constrained programming approach. The best neighborhood solution is selected as the next iterate. At each iteration, the method searches for the best candidate in some neighborhoods of the current solution. In order to avoid cycles, the algorithm keeps a dynamical list of prohibited moves and at some point, migrates to a solution that is worse than the current solution.
Several studies have been carried out previously to solve NRP but there is no one solution technique that can be considered as the best [23]. As an effort, some of the recent works [10,24] attempted to solve NRP by using various search techniques, including TS with its efficiency and success as discussed earlier. However, the work by [8] suggested that improvement on neighborhoods and smart intensification could produce faster and more fitted output. Hence, it has motivated the work in this paper, which strived to explore on the improvement of the neighborhoods for the NRP and thus, suggests a promising solution approach. It discusses how exploitations on the neighborhoods in relation to TS approach are taken advantage to solve the NRP. Moreover, this study also introduced a semi-random initialization method to initiate a solution. The advantage of using this method is that it avoids the violation of hard constraints whereas in other initialization method such as greedy initialization, it cannot guarantee the hard constraints compliance.
A description on the real world NRP and the TS approach are explained in Section 2 and Section 3. Section 4 provides the implementation and analysis of the results. Finally, the conclusion is provided in Section 5 with some future directions.
2 The real-world NRP
This study focuses on a case study that has been examined by [25] in a general hospital in Malaysia. The aim is to generate a two weeks nurse schedule and at the same time focusing on producing a good quality roster. The number of nurses considered in this study is 39, which is a large ward at a Malaysian general hospital. There are three different shift types in a day: morning (M), evening (E) and night (N) shifts. The M and E shifts are regular shifts, which carry seven or eight hours of nursing duties. The N shift can be varied with equal to or longer hours than the M or the E shifts. For instance, the M shift can start from 7.00 am to 2.00 pm, the E shift can start from 2.00 pm to 9.00 pm, and the N shift can be from 9.00 pm to 7.00 am.
Each nurse can be assigned to only one shift per day and normally the overtime shift is not allowed. In this environment, it is possible that there is no official allocation of rest or meal breaks during work shifts. Subsequently, nurses can take their meals in their units only and within that shift hours depending on allowable situations. Due to this restriction, this study will not consider the meal breaks allocation. The objective of this study is to develop a nurse roster that satisfies the nurses preferences as much as possible hence, the job satisfaction among the nurses is increased.
The following rules are considered as hard constraints and must always be met to generate feasible and acceptable roster.
-
Each nurse cannot work more than k consecutive days.
-
Assign each week a weekly off-day.
-
Avoidance of working shift patterns that might adversely affect nurses health.
-
Minimum nurse skill level required for each working shift.
-
Each nurse takes on only one working shift.
-
Minimum number of night shifts.
-
Every nurse is not permitted to work night shifts followed by morning shifts or evening shifts.
-
The roster must follow the biological clock. For example, night shift should follow after evening shift and evening shift should follow after morning shift.
In order to evaluate the quality of the obtained schedule, the following soft constraints are considered:
-
The nurse preferences for longer off days.
-
Avoid assigning a morning shift or evening shift followed by a night shift.
-
Avoid isolated working shifts or off days.
-
A balanced number of mornings, evening and night shifts must be made available to all the nurses through the coverage over the assignment of nurses in different shifts in a day in each skill level.
Details of further descriptions of the constraints are discussed below.
Mandatory workdays constraints. The fulltime nurses must get one day off per week. Therefore, they need to work six days in a week. Other special days off also occurred that followed after the existence of N shifts.
-
Covering constraints. The required number of nurses for each shift and for each skill level in a day has to be met. This is really a hard constraint and a unit would operate inefficiently without it.
-
Work stretch constraints. In the nurses personal schedules, consecutive work days must not exceed certain maximum days and must not be less than the minimum days limit. If this constraint is violated, the maximum work stretch will exhaust the nurses and the minimum work stretch will create uneasiness and reluctance on their part to go to work.
-
Ordering constraints. The quality of the schedule is reflected by the assigning of the shifts in a particular order. Therefore, the nurses well-being can be assured. The sequence of shifts in a day is in the order of M → E → N. It means M must occur before E and E must occur before N. The reversed sequence is forbidden because to respect the monotonic or circadian rhythm rule.
-
Pre-assigned constraints. Three N shifts start the assigned shifts in cyclic order. Then two nights off (NO) days are assigned following the three night shifts, as shown in Figure 1. Note that a nurse must have a day off after working for three consecutive night shifts [16]. This pre-assigned constraint is in staggered and rotation manner. Therefore, every nurse gets an equal number of N shifts, in such a way that they are equitably distributed throughout the planning horizon.

Figure 1 The allocation of N and NO.
-
Split days off constraints. Split days off is defined when any two off days are separated by a single working day. This formation is forbidden and needs to be avoided because it promotes negative effects on the nurses, such as feelings of unfairness, laziness and absenteeism [25].
There are several specifications that are considered in this study such as the design of shifts, types of off days and category of nurses.
-
Design of shifts. The N shifts has assigned in cyclic order in the beginning of the scheduling process, so the M and E work stretches are assigned together, followed by this assigning process. Therefore, it must observe the distributions of M and E shifts across a scheduling period. The M and E shifts are expected to be equivalent for each nurse.
-
Types of off days. Three types of off days are: night off day (NO), weekly off day (WO) and, public off day (PO). The two NO is automatically followed by the three N shifts for every cyclic order. WO is one day off weekly for each nurse. Other types can be PO (holidays), which generally are distributed in a year or some special occasion holidays. It shows that consecutive days off are much preferred by every nurse whenever possible.
-
Categories of nurses. The ward represents a typical scheduling problem evident in many large hospitals throughout Malaysia, including privately operated and teaching hospitals. The ward is determined to improve the quality of services provided through the increase in the number of higher skill grade staff and the freezing of lower skill grade staff intake. Therefore, the whole staff nurses are re-categorized into experienced and less experienced sub-groups or also known as senior and junior level [25].
3 Tabu search architecture
As a meta-heuristic approach, the TS technique consists of building blocks which are identified as neighborhoods, short term memory (embodied in the tabu list), long term memory and aspiration criteria [20]. [18] defined that the most important distinguishing property of the TS is the exploitation of adaptive form of memory. These take the form of short-term memory strategies (i.e., tabu list and aspiration criteria) and long-term memory strategies (e.g., intensification and diversification). This section explains on the solution representation, initialization strategy, fitness evaluation, neighbourhood generation and tabu search approach.
3.1 Solution representation
The construction of the nurse schedule is a two-dimensional matrix configure, in which the rows represent the nurse personal schedules (n i ) and the columns represent the days (d j ) in the scheduling period as presented in Figure 2. The row is divided into two levels; consisting of the junior and senior levels. The number of nurses can be adjusted. The dimensions of the matrix depend on the number of nurses and the number of days. The elements assigned in the matrix cells are representation of working shifts and the appropriate off days.
 |
Figure 2 The solution encoding and representation. |
3.2 Initialization of solution
In this paper, a semi random initialization is introduced to get a high-quality initial solution to maximize the satisfaction of nurse preferences. The semi-random initialization start is to give the nurses exactly the schedules they want. This indicates the nurses assigned to work in their rotations and any shifts that they requested. Therefore, it can improve the job satisfaction among the nurses and it can also meet the hospitals requirements. All these allocations are based on the hard constraints as discussed earlier in Section 2. To generate that initial solution, some heuristics were used to develop flexible and reliable solutions relevant to an actual hospital situation.
Firstly, the three N shifts start with the assignment in cyclic order. Then the assignment of two NO days follows the three N shifts. Next, one WO day is assigned randomly for every week. Assign in front of the WO day with one PO day for every two weeks. Therefore, it can generate longer consecutive days off such that it fulfils nurse preferences.
The other working shifts are M and E shifts which are assigned together for each row in the schedule. They fill up the empty cells randomly with M and E work stretches based on circadian rules obtained from a list. This is also depending on the available cell blocks and work stretch constraints [25]. Every nurse is assigned the working shifts with satisfying working shift type [16]. The patterns of M and E shifts must satisfy the nurses preferences. Furthermore, the numbers of M and E shifts are also equivalent for every nurse.
The advantage of using this method is that it avoids the violation of hard constraints whereas in other initialization method such as greedy initialization, it cannot guarantee that the hard constraints are not violated. Next, the fitness evaluation is used to evaluate the completed nurse schedule, as discussed in the following subsection. The components count, record and give penalty values or weights to the respective violations. The initial schedule considered the hard violations and the weights are given to the soft violation that occurs in the solution.
3.3 Fitness evaluation
The penalty levels set depend on the aspiration of the whole workable schedule. However, this aspiration level can be appropriately determined through the schedulers vast experience (e.g. the head nurse). The objective function can be presented in two aspects in which the targeted hard requirements and soft preference constraints violation are merged. The function can be viewed as the vertical and horizontal checks of a schedule [25]. The general objective function for the schedule f(s) is shown in equation (1), and the weight penalty constraint type q is w
q
with the number of constraints violation for type q in the schedule, where s becomes: (1)
C
q
(s) is the overall function in equation (2). The function in equation (2) is embedded in equation (1). The number of constraints violation for type p in the schedule is zero, c
q
(s) = 0 if there is no violation constraint type q. The description of function in equation (2) is given as follows:
(1)
C
q
(s) is the overall function in equation (2). The function in equation (2) is embedded in equation (1). The number of constraints violation for type p in the schedule is zero, c
q
(s) = 0 if there is no violation constraint type q. The description of function in equation (2) is given as follows:
Parameter:
I = number of nurses;
P = number of skill levels;
J = number of days in the scheduling period;
Q = number of constraint types;
M = number of possible shifts patterns;
w pim = weight or penalty cost for the relative decision variable b pim;
w pjq = weight or penalty cost for the relative constraint c pjq;
w iq = weight or penalty cost for the relative constraint c iq;
Objective functions:
The fitness function is reflected in the following three objectives as follows:
Objective 1: To minimize the imbalances of coverage over the assignment of nurses in different shifts in a day in each skill level. In other words, to maximize the number of nurses assigned to each shift (nurse coverage) in each skill level.
Objective 2: To minimize the nurses dislike (negative preferences) over shifts arrangement.
Objective 3: To minimize the deviation in the number of different shifts arrangement for each nurse. In other word, to ensure equitable shifts distribution.
Hence, the overall objective function Z s of a solution s is the sum of three sub-functions as follows:
Based on the intuitive judgment by [25], the relative penalty costs are chosen in such a way that they reflect the relative importance of dissatisfying different kinds of constraint. The idea is that, the higher penalty cost, the higher is the pressure for the TS operator to remove the constraint, or even discards the affected individual.
The first objective is to minimize the imbalances of coverage over the assignment of nurses in different shifts in a day in each skill level. The penalty values, w pim are to evaluate the relative decision variable of b pim where the violation of each decision variable is given a value of 100.
The second objective of the algorithm is to minimize the number of hard and soft constraint violations for each nurse. The penalty values, w pjq are to evaluate constraints for every row (nurse) and are given in Table 1. The total number of the M and E shifts in a personal roster of the nurses (the rows) should roughly be equivalent. Moreover, the days off are strongly preferred to be consecutive in the arrangement.
The third objective of the algorithm is to minimize the number of hard and soft constraint violations for each day, as shown in Table 2. The penalty values, w iq to evaluate constraints for every column (day). There must be at least 3 nurses assigned for each shift type, for each nurse skill level on each day. Hence, the high penalty is given if there is less shift type in each day.
Evaluation constraints for every row.
Evaluation constraints for every column.
3.4 Neighborhood generation
This study introduced a special neighborhood generation method in the TS algorithm, which is specific to the NRP. Two ways of neighborhood generation process were introduced which are the nurse skill level swap, W(l) and shift pattern swap, W(p).
3.4.1 Nurses skill level swap
The first method is by swapping a row in junior skill level with a row in senior skill level, which at the same time does not violate night shift constraint. A row represent a particular nurse roster throughout the scheduling period of two weeks, as shown in Figure 3.
Nurse skill level swap, W(l) is done by swapping a row in junior skill level with a row in senior skill level, which at the same time does not violate the night shift constraint, a row represent a particular nurse roster throughout the scheduling period of two weeks. This is based on assignment of at least three nurses for each shift type, for each nurse skill level on each day. The nurse skill level consists of both the senior level and junior level. The possible problem which occurs in the two weeks of NRP is not enough shift types for the nurse skill level.
There must be at least three nurses for every shift type (morning, evening and night) in each day. The problem occurs because the assigning work days and off days are in row by row, considering the hard and soft constraints. The night shift type is enough for each day because the three night shifts are assigned in cyclic order. The other types of work days such as the morning and evening shifts are not enough for a few days, mainly for the senior nurse level only because the number of senior nurse level is smaller than the number of junior nurse level.
In order to execute enough shift types for the senior nurse level, swapping the arrangement of work days and off days is done. The swapping is done between the senior nurse level with the senior nurse level and both nurses have the same cyclic night shift order, as shown in Figure 3.
 |
Figure 3 The possible representation of solution W(l) for a partial solution. |
3.4.2 Shift pattern swap
The second way is shift pattern swap. In this swapping method we exchange shift patterns with equivalent length. The shifts types involve in the pattern are only M and E shifts, as shown in Figure 4. The moves may be equivalent to the total number of morning and evening shifts.
Next, choose the best neighbor with the minimum total penalty. The unwanted schedule in the iteration will keep in the empty tabu list. The length of tabu tenure is six. Therefore, the sequence of unwanted schedule saves for a while (short term memory) by first in and first out (FIFO) keeping process [26,27]. Then, the unwanted schedule will keep in the garbage if the tabu list is full. The unwanted schedule in the tabu list can be used to the next iteration if it is better in terms of the objective function value compared to the current schedule. This process is called aspiration criterion.
The morning and evening shifts are assigned together in the schedule. The pattern of shift pattern swap W(p) is based on the nurse preferences. In this swapping method we exchange shift patterns with equivalent length. The shifts types involve in the pattern are only M and E shifts. The problem occurs because there are many available patterns of morning and evening shifts which are assigned to a null cell in the initial schedule. The total number of morning and evening shifts in a few personal rosters is not roughly equivalent. The way to execute this problem is by moving between the two patterns of morning and evening shifts that is the same number of morning and evening shift blocks and different personal roster, as shown in Figure 5. The moves may be equivalent to the total number of morning and evening shifts.
All the hard and soft constraints are considered at all moves (neighborhood). The number of shift types (morning, evening and night) may be roughly balanced in each personal roster (nurse) and in each day.
 |
Figure 4 The possible representation of solution W(p) for a partial solution. |
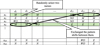 |
Figure 5 The possible representation of solution W(p) for a partial solution. |
3.5 Tabu list
Figure 6 shows the process of tabu list in the TS algorithm. Once the iteration started, a sequence of several schedules was generated by the neighborhood process. Then, the next iteration was continued by generating the best schedule from the current neighborhood process. The empty tabu list, t will keep the unwanted schedule in the iteration. The length of suggested list (tabu tenure) is six lists [26,27]. Therefore, the sequence of unwanted schedule was saved a while (short term memory) by first in and first out (FIFO) keeping processes. Then, the unwanted schedule will keep in the garbage if the tabu list is full. The unwanted schedule in the tabu list can be used to the next iteration if it is better compared to the current schedule, and this process is called the aspiration criterion.
 |
Figure 6 The proposed tabu search algorithm for nurse rostering problem. |
3.6 Aspiration criterion
Figure 6 shows the process of aspiration criterion in the TS algorithm. The aspiration criterion process is started once the iteration process is set. This process begins with choosing the minimum unwanted schedule in the tabu list ( ). Then, compare the minimum unwanted schedule (
). Then, compare the minimum unwanted schedule ( ) with the current best schedule (minA
i
). If the unwanted schedule in the tabu list is better than the current best schedule (
) with the current best schedule (minA
i
). If the unwanted schedule in the tabu list is better than the current best schedule (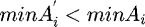 ), the
), the 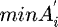 schedule is be chosen to create the neighborhood process and vice versa. This procedure is adopted from [20].
schedule is be chosen to create the neighborhood process and vice versa. This procedure is adopted from [20].
4 Implementation and result
The TS model is tested for 30 samples of different initial schedules. This model searches for the best feasible solution based on objective function. The operation stopped until there is no more improvement to the current local optimum schedule, after several consecutive iterations. The best so far schedule sample in the experiment is shown in Figure 7. The initial solution is improved through the neighborhood generation process for a number of iterations. The initial solution, 1230 is improved to the best solution grand total penalty is 1040. Figure 8 shows the grand total penalty from starting initial solution (1230) to the best solution (1040) and there is no more improvement after 111 iterations.
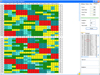 |
Figure 7 The ‘best so far' schedule sample. |
 |
Figure 8 The sample grand total penalty. |
4.1 Comparison techniques
The performance of the proposed TS model is compared with the manual result schedule and was provided by the one of the general hospitals. This is an actual nurse schedule and original problem that had been developed by the head nurse. Moreover, the original problem parameters were reconstructed and fed into the TS technique system. Furthermore, the TS model was also compared with the Memetic Algorithm (MA) model. This model was developed by [25]. Besides, the TS model has considered the constraints excerpted from this literature.
Table 3 shows the summary of the whole results. The comparison for each result based on manual result. The results for the human generated (HG) technique were made possible after a series of long observations and discussions with the hospitals management. The results for the MA model were discovered from the best so far schedule shown in [25].
Table 3 shows the results based on different criteria for models comparison. This table only answers the questions qualitatively. The manual or HG model and the MA model are compared to our proposed TS technique. This HG technique is currently practiced in many general and private hospitals throughout Malaysia.
Coverage is measured based on the violation of the hard constraints. Each model considered the hard constraint in the initial schedule process. The ability of the approach to satisfy the minimum coverage requirements of the staffing is such as a nurse is allowed to work only one shift a day. Yes for every model because every schedule fulfills the objective. Furthermore, in terms of the ability of each scheduling approach to provide balanced coverage is such as to ensure that each work shift is provided with the correct number of nurses, so that any workload could be distributed fairly and evenly. Moderately balanced for both TS and MA models because these approaches satisfied the covering constraint in the initial process, however, they need to be adjusted in the final stage of the process. It is time consuming for the HG model to satisfy the covering constraints since it is done manually. Therefore, the HG model is given No for balanced coverage criterion.
Then, quality is measured based on the violation of the soft constraints. It can be the most important criterion for our judgment as it relates to the perceived value of the roster to the nurses. In our case, there are lists of attributes, which both TS and MA models consider under this criterion as many as possible in the initial schedule process. Therefore, the TS and MA models are given the positive answer compared to the HG model. Both TS and MA models are Moderately fair because these models attempted to distribute shifts equally in as much as possible.
While flexibility was measured in terms of how flexible each scheduling approach was in adapting to change in the scheduling environment. The common changes are the ones that involve the staffing level requirements. This TS model can adjust the number of nurses for the senior or junior level.
Finally, the real cost is not relevant to this scheduling environment, it was satisfying to measure the cost in terms of the time required to construct this bi-weekly roster using each scheduling approach. In addition, the cost was also measured in terms of the available category of the nursing staff required to construct the roster under each approach. Both TS and MA models used computerized process. Therefore, any senior staff can construct the nurse schedule. In addition, these models required less amount of time in constructing the nurse schedule as compared to the HG model. Nevertheless, TS shows faster than the MA since TS is a local search-based approach which requires only a single initial solution to be evaluated and improved iteratively while MA is a population-based approach which incorporates multiple initial solutions.
Results based on different criteria for models comparison (TS model = our approach, MA model = Memetic Algorithm model by Ramli (2004) and HG model = manual approach).
5 Conclusion
In this study, the nurse scheduling system is developed and can generate the diversification of the nurse schedule improvement. The combination of the two different neighborhoods has been implemented to improve the generation of the nurse schedule diversification. The adoption of the innovative neighbour generation heuristics has helped in the diversification of solution search. The rostering process took a short time to generate effective and efficient rosters satisfying both hard and soft constraints relevant to the problem. The system is able to fulfil circadian rhythm ordering when generating rosters thus, satisfying the body clock requirement which helps to avoid body fatigue. Moreover, it is also able to schedule shift work within the policy day limit which in turn promotes fairness to nurses. The rostering system is efficient and able to properly utilize the nursing manpower. Thus, it is able to minimize cost in term of idle staff. The system can be used to assist nurse managers in generating shift work rosters for nurses in a hospital unit whithin limited time. Overall, rosters produced through the proposed TS technique are of high quality and without bias. In this sense, it is certainly better than the manually constructed rosters. In future, this TS technique can be enhanced by hybridizing it with other population-based techniques [11,13,14] since it shows promising results in solving NRP. Furthermore, we intend to test the proposed approach on other benchmark datasets of NRP.
Acknowledgments
This research has been supported by the Ministry of Higher Education of Malaysia under the MyBrain15 program and a joint research program with Bina Nusantara University.
References
- J. Van den Bergh, J. Beliën, P. De Bruecker, E. Demeulemeester, L. De Boeck, Personnel scheduling: A literature review, Eur. J. Operat. Res. 226, 367–385 (2013) [CrossRef] [Google Scholar]
- E.K. Burke, G. Kendall, E. Soubeiga, A tabu-search hyper-heuristic for timetabling and rostering, J. Heuristics 9, 451–470 (2003) [CrossRef] [Google Scholar]
- P. Brucker, R. Qu, E. Burke, G. Post, A decomposition, construction and post-processing approach for nurse rostering, Multidisciplinary International Scheduling Conference MISTA 2005 , pp. 397–406 (2007) [Google Scholar]
- M.N. Azaiez, S.S. Al Sharif, A 0-1 goal programming model for nurse scheduling. Comput. Operat. Res. 32, 491–507 (2005) [CrossRef] [Google Scholar]
- T.I. Wickert, P. Smet, G.V. Berghe, The nurse rerostering problem: Strategies for reconstructing disrupted schedules, Comput. Operat. Res. 104, 319–337 (2019) [CrossRef] [Google Scholar]
- F. He, R. Qu, A constraint programming based column generation approach to nurse rostering problems, Comput. Operat. Res. 39, 3331–3343 (2012) [CrossRef] [Google Scholar]
- S. Abdennadher, H. Schlenker, Interdip − an interactive constraint based nurse scheduler. Proceedings of The First International Conference and Exhibition on The Practical Application of Constraint Technologies and Logic Programming, London , 1999 [Google Scholar]
- A. Oughalime, W.R. Ismail, L.C. Yeun, A tabu search approach to the nurse scheduling problem. International Symposium on Information Technology, Kuala Lumpur , 2008 [Google Scholar]
- Z. Liu, Z. Liu, Z. Zhu, Y. Shen, J. Dong, Simulated annealing for a multi-level nurse rostering problem in hemodialysis service, Appl. Soft Comput. 64, 148–160 (2018) [CrossRef] [Google Scholar]
- U. Aickelin, K.A. Dowsland, An indirect genetic algorithm for a nurse-scheduling problem, Comput. Operat. Res. 31, 761–778 (2004) [CrossRef] [Google Scholar]
- M.A. Awadallah, A.L. Bolaji, M.A. Al-Betar, A hybrid artificial bee colony for a nurse rostering problem. Appl. Soft Comput. 35, 726–739 (2015) [CrossRef] [Google Scholar]
- E. Özcan Memes, Self-generation and nurse rostering, in E. K. Burke & H. Rudová (Eds.), Practice and Theory of Automated Timetabling VI. PATAT 2006. Lecture Notes in Computer Science, 3867 (Berlin, Springer, 2007), pp. 85–104 [Google Scholar]
- T-H. Wu, J-Y. Yeh, Y-M. Lee, A particle swarm optimization approach with refinement procedure for nurse rostering problem, Comput. Operat. Res. 54, 52–63 (2015) [CrossRef] [Google Scholar]
- M. Hadwan, M. Ayob, N.R. Sabar, R. Qu, A harmony search algorithm for nurse rostering problems, Inf. Sci. 233, 126–140 (2013) [CrossRef] [Google Scholar]
- R.A.M. Gomes, T.A.M. Toffolo, H.G. Santos, Variable neighborhood search accelerated column generation for the nurse rostering problem. Electron. Notes Discr. Math. 58, 31–38 (2017) [CrossRef] [Google Scholar]
- C. Valouxis, E. Housos, Hybrid optimization techniques for the workshift and rest assignment of nursing personnel, Artif. Intell. Med. 20, 155–175 (2000) [CrossRef] [PubMed] [Google Scholar]
- M. Hidayati, A. Wibowo, S. Abdul-Rahman, Preliminary review on population based approaches for physician scheduling, Proceedings of 2018 Indonesian Association for Pattern Recognition International Conference (INAPR), Jakarta, Indonesia , 2018, pp. 90–94 [CrossRef] [Google Scholar]
- F. Glover, M. Laguna, Tabu search (Kluwer Academic Publisher, Boston, 1997) [CrossRef] [Google Scholar]
- T. Dias, D. Ferber, C. Souza, A. Moura, Constructing nurse schedules at large hospitals, Int. Trans. Operat. Res. 10, 245–265 (2003) [CrossRef] [Google Scholar]
- K. Nonobe, T. Ibaraki, A tabu search approach to the constraint satisfaction problem as a general problem solver, Eur. J. Operat. Res. 106, 599–623 (1998) [CrossRef] [Google Scholar]
- K. Dowsland, Nurse scheduling with tabu search and strategic oscillation, Eur. J. Operat. Res. 106, 393–407 (1998) [CrossRef] [Google Scholar]
- E. Burke, P. De Causmaecker, G. Vanden Berghe, A hybrid tabu search algorithm for the nurse rostering problem, in: B. McKay, X. Yao, C.S. Newton, J.H. Kim, T. Furuhashi (Eds.), Simulated Evolution and Learning. SEAL 1998. Lecture Notes in Computer Science 1585 , Springer, Berlin, Heidelberg, 1999, pp. 187–194 [Google Scholar]
- H.H. Millar, M. Kiragu, Cyclic and non-cyclic scheduling of 12 h shift nurses by network programming, Eur. J. Operat. Res. 104, 582–592 (1998) [CrossRef] [Google Scholar]
- B. Cheang, H. Li, A. Lim, B. Rodrigues, Nurse rostering problems: a bibliographic survey, Eur. J. Operat. Res. 151, 447–460 (2003) [CrossRef] [Google Scholar]
- R. Ramli, An evolutionary algorithm for the nurse scheduling problem with circadian rhythms, Unpublished PhD Thesis, Universiti Sains Malaysia, Malaysia, 2004 [Google Scholar]
- F. Bellanti, G. Carello, F.D. Croce, R. Tadei, A geedy-based neighborhood search approach to a nurse rostering problem, Eur. J. Operat. Res. 153, 28–40 (2004) [CrossRef] [Google Scholar]
- F. Bellanti, G. Carello, F.D. Croce, R. Tadei, A tabu search approach to a nurse rostering problem, Proceedings of the 4th Metaheuristics International Conference, MIC 2001, pp. 165–167 [Google Scholar]
Cite this article as: Razamin Ramli, Siti Nurin Ima Ahmad, Syariza Abdul-Rahman, Antoni Wibowo, A tabu search approach with embedded nurse preferences for solving nurse rostering problem, Int. J. Simul. Multidisci. Des. Optim. 11, 10 (2020)
All Tables
Results based on different criteria for models comparison (TS model = our approach, MA model = Memetic Algorithm model by Ramli (2004) and HG model = manual approach).
All Figures
 |
Figure 1 The allocation of N and NO. |
| In the text | |
 |
Figure 2 The solution encoding and representation. |
| In the text | |
 |
Figure 3 The possible representation of solution W(l) for a partial solution. |
| In the text | |
 |
Figure 4 The possible representation of solution W(p) for a partial solution. |
| In the text | |
 |
Figure 5 The possible representation of solution W(p) for a partial solution. |
| In the text | |
 |
Figure 6 The proposed tabu search algorithm for nurse rostering problem. |
| In the text | |
 |
Figure 7 The ‘best so far' schedule sample. |
| In the text | |
 |
Figure 8 The sample grand total penalty. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.