EDP Sciences logo
Submit your paper
Search
Menu
Home All issues Volume 6 (2015) Int. J. Simul. Multisci. Des. Optim., 6 (2015) A6 Full HTML
Open Access
Issue
Int. J. Simul. Multisci. Des. Optim.
Volume 6, 2015
Article Number A6
Number of page(s) 6
DOI https://doi.org/10.1051/smdo/2015006
Published online 23 December 2015

© S.E. Gulebaglan et al., Published by EDP Sciences, 2015

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

Alkali hydrides (LiH, NaH, KH, RbH and CsH) have possible applications in nuclear and chemical industries [1]. Thus, this materials have been investigated both experimentally and theoretically for many years. Like alkali metal halides, alkali metal hydrides crystallize with the rock-salt structure. The X-ray experimental study [2] showed that RbH crystallize with the rock-salt (B1) structure at room temperature. Gaydon and Pearse [3] studied the band structure of RbH experimentally and theoretically. A structural phase transition from NaCl to CsCl phase was observed in RbH at high pressure [4]. Jain [5] investigated ground state of RbH using the Rydberg-Klein-Ress method. Stwalley et al. [6] reported structure of the alkali hydride diatomic molecules. Hooper and Zurek [7] investigated the structures of compressed rubidium polyhydrides, RbHn with n > 1. Zrafi et al. [8] calculated the evaluation of the first and second derivative of nonadiabatic coupling between the several adiabatic states of LiH, RbH and CsH molecules. Ahuja [9] investigated the structure of RbH under high compressions by means of first principles self consistent total-energy calculations within local-density approximation. Fatmi et al. [10] showed structural, electronic, optical and thermodynamic properties of NaxRb1−xH and NaxK1−xH alloys. Hooper et al. [11] discussed three new structures of high-pressure alkali metal hydrides (P63/mmc, I4I/amd, and Pnma) and found structural phase transitions via evolutionary methodologies. Sudha Priyonga et al. [12] calculated structural, electronic and elastic properties of alkali hydrides (MH: M = Li, Na, K, Rb, Cs).

2 Computational methods

The first-principles calculations are performed with the ABINIT [13] and the WIEN2K [14] code programs. The structural, electronic and optical properties of RbH crystal was investigated using WIEN2K package within the Generalized Gradient Approximation (GGA) based on the density functional theory (DFT). 286 k points were applied in the Brillouin zone for the structural, electronic and optical properties of RbH crystal.

In addition, the dynamic and thermodynamic properties of RbH crystal was investigated using ABINIT code. The calculated results were obtained using GGA included the exchange-correlation effects [15] of DFT. The self-consistent norm-conserving pseudopotentials of FHI-type with a Troullier-Martins scheme [16] for all atoms of RbH crystal were used. The Kohn-Sham equations [17] were solved the conjugate gradient minimization method [18]. Plane waves were used for the electronic wave functions. For the true valence electron of Rubidium atom and for Hydrogen atom were deliberated the 5s electron and the 1s electron, respectively. Firstly, in all calculations total energy of this material was accommodated with respect to cutoff energy and Monkhorst-Pack mesh grid. The calculated total energy calculations were done to a good convergence at 30 hartree of cutoff energy. Besides, 60k points using 6 × 6 × 6 Monkhorst-Pack mesh grid [19] in RbH crystal for structural optimization and the calculations of dynamic and thermodynamic properties.

3 Structural and electronic properties

RbH crystal contains two atoms per face centered cubic unit cell and crystallizes in the Rock salt-type structure. Rb atom is centered at (0, 0, 0) and H atom is located at (0.5, 0.5, 0.5) in the reduced coordinates. The volume of unit cell is optimized using WIEN2K code. The total energy of RbAu compound has been investigated as a function of the unit cell volume and fitted to the Murnaghan equation. Volume parameter was calculated as 376.39 (a.u3) of cubic atomic. In this value, the total force is equal to zero at minimum total energy. The calculated values of lattice parameters for RbH compound is 11.461 bohr (6.064 Å), while experimental value is 6.037 Å [2]. As seen, there is a good agreement between calculated and experimental result for lattice parameters. Then, calculated result was used for calculation of all studied physical properties of this compound (Table 1).

Table 1.

Calculated lattice parameter a0 (Å) and energy gap Eg (eV).

The pseudopotential method based on density functional theory within general gradient approximation was used for electronic structure calculations of RbH. According to the band structure calculations, RbH crystal has a direct band gap at high symmetry point L with the value of 2.943 eV and experimental values are 2.96 eV. We found that RbH is a semiconductor. Electronic band structure was plotted as in Figure 1.

thumbnail Figure 1.

Plotted electronic band structure for RbH.

4 Optical properties

RbH crystal is a cubic crystal and space group number is 216. This structure is requested to investigate one dielectric component. Our calculation were performed 0–40 eV photon energy range. The calculated real (ε1) and imaginary (ε2) parts of dielectric function of this compound are illustrated in Figure 2. As seen from this figure, the real part of dielectric function, ε1, goes to its maximum value at 4.8 eV of photon energy for RbH. There is no absorption through 2.93 eV. After this value, optic transitions from valance band to conduction band can be detected. Furthermore, real part goes to zero at 20.3133, 20.69429, 20.80311, 21.94599 and 21.9732 eV. The incident electromagnetic waves are completely reflected at the negative values of real part. The reflectivity (R) and absorption (α) active regions are from 12 eV to 24 eV and from 2 eV to 18 eV, respectively. The extinction coefficient (k) varies similar to the absorption coefficient (α). The region of the active damping is between 2 eV and 18 eV. Refractive index (n) is 1.75 for low and very low energy electromagnetic waves. The range of the optical loss in surface and volume is maximum in the ultraviolet region of the electromagnetic spectrum. The calculated extinction coefficient, absorption coefficient, reflectivity and refractive index (n) for RbH are shown in Figures 3 and 4, respectively. The spectral dependence of calculated refractive index is in the wavelength range of 0–0.6 μm, and the calculated value of refractive indices is 1.75 for RbH. The energy loss functions (L), for both surface and volume, are illustrated in Figure 5. As seen in Figure 5, sharp peaks are incorporated with plasma oscillations concerned to the photon energy values.

thumbnail Figure 2.

Real and imaginary parts of dielectric function for RbH.

thumbnail Figure 3.

Calculated (a) reflectivity spectrum (R), (b) absorption (α) coefficient and (c) extinction coefficient (k) for RbH.

thumbnail Figure 4.

The calculated spectral dependence of refractive index (n) on wavelength of RbH.

thumbnail Figure 5.

Volume and surface loss functions (L) for RbH as a function of photon energy for RbAu.

5 Elastic properties

To obtain elastic constants of this compound, we used the method developed by Morteza Jamal integrated in WIEN2 K code [24]. Here, to analyze the elastic properties, we calculated the elastic constants (Cij), Young module, shear modulus, bulk modulus, and Poisson’s coefficients with three different approximations that are namely Voight, Reuss and Hill using the mentioned method in reference [23]. The elastic constants are calculated to be C11 = 32.835 GPa, C12 = 3.815 GPa, and C44 = 9.657 GPa for RbH. In this case, RbH has a stable structure. The calculated elastic constants of RbH are listed in Table 2. The Born mechanical stability criteria for cubic structure is given below: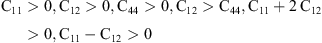

Table 2.

Calculated elastic constants for RbH with NaCl structure.

The Young’s modulus E, Zener anisotropy factor A and Poisson’s ratio ν, which have the plenty of exciting elastic properties for applications, are also computed in terms of the reckoned data using the following relations: 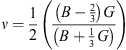and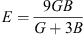where G = (GV + GR)/2 is the isotropic shear modulus. The GV (GV = (C11  − C12 + 3 C44)/5) is Voigt’s shear modulus concerned to the upstairs bound of G values, and GR (5/GR = 4/(C11 C12) + 3/C44) the Reuss’s shear modulus concerned to the lower bound of G values. The calculated Zener anisotropy factor, Poisson’s ratio, Young’s modulus, and shear modulus for RbH are given in Table 3. The calculated and other results are in a good agreement.

Table 3.

Calculated single crystal bulk modulus (B0), Young modulus (E), shear modulus (G), anisotropy factor (A), Poisson’s ratio (ν) obtained for RbH.

6 Dynamic properties

Phonon dispersion curves and phonon density of states of RbH along the high-symmetry directions are calculated by using the ABINIT. In RbH crystal, unit cell involves two atoms at zero pressure. The Rb atom and H atom are positioned at the point of (0.0, 0.0, 0.0) and (0.5, 0.5, 0.5) at zero pressure, respectively. The computed phonon dispersion curves of RbH, along the main symmetry direction of the Brillouin zone are illustrated in Figure 6. RbH has two atoms per unit cell so that six phonon branches occur. Three of them are acoustic and three of them are optical branches. Some of the branches are degenerate along more symmetrical directions (Γ-X and Γ-L) inside Brillouin zone of RbH crystal. The calculated phonon frequencies resulting from the high symmetry points (Γ, X and L) of the Brillouin zone are listed in Table 4.

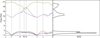thumbnail Figure 6.

Phonon dispersion curves and phonon density of states for RbH.

Table 4.

The calculated phonon frequencies at Γ, X and L points for RbH.

There is a gap between the acoustic and the optic phonon branches which shows that RbH is a phononic crystal. Optical branches are almost horizontal around Г symmetry point. Optical and acoustic branches degenerate at left and right side of Г point. All branches are non-degenerate between X-W, W-K, K-Г points. Slopes of acoustic branches around Г point are steep, which shows large elastic constant for RbH. High phonon frequencies are attributed to H atoms, because its mass is small and can vibrate very rapidly.

7 Thermodynamic properties

After calculating the phonon band structure, we have inquired the thermodynamic properties of RbH using these phonon band structure calculations. In terms of thermodynamic properties, we have examined the entropy, constant-volume specific heat and the phonon contributions to the Helmholtz free energy and internal energy. We have plotted all these thermodynamic quantities as functions of temperature as can be seen in Figure 7. As seen from this figure, the values of free energy and internal energy are different from zero at zero temperature which shows zero point oscillations. The values of free energy and internal energy at zero temperature are very close to each other that is 9.92 kJ/mol for free energy and 10.47 kJ/mol for internal energy. The constant-volume specific heat of RbH approaches a limit value of 49.34 J/mol K at 1466.30 K.

thumbnail Figure 7.

(a) Phonon contribution to the free energy as a function of temperature, (b) phonon contribution to the internal energy, (c) the entropy as a function of temperature and (d) constant volume specific heat as a function of temperature, as a function of temperature for RbAu.

8 Conclusion

We have investigated the dynamic and thermodynamic properties of Rubidium Hydride (RbH) by an ab-initio pseudopotential method applying density functional theory within the generalized gradient approximation. RbH show semiconducting property and the value of band gap is 2.943 eV. We have declared real and imaginary parts of dielectric function, reflectivity spectrum, absorption coefficient, extinction coefficient and loss function as a function of photon energy and refractive index as a function of photon wavelength. During the investigation of dynamical properties of RbH, we have calculated and plotted phonon density of states function graphs. While examining the thermodynamic properties of RbH, we have calculated the phonon contribution to the Helmholtz free energy and to the internal energy, the entropy and constant-volume specific heat as functions of temperature.

References

  1. Latroche MJ. 2004. Structural and thermodynamic properties of metallic hydrides used for energy storage. Phys. Chem. Solids, 65, 517. [CrossRef] [Google Scholar]
  2. Zinti E, Harder A. 1931. Uber Alkalihydride. Z. Phys. Chem. Abt. B, 14, 265. [Google Scholar]
  3. Gaydon AG, Pearse RWB. 1939. The spectrum of rubidium hydride, RbH. II. Potential curves, wave functions and intensity distribution. Proc. Roy. Soc. A, 173, 28–37, 37–47. [CrossRef] [Google Scholar]
  4. Hochheimer HD, Strossner K, Hale W, Baronowski B. 1987. High-pressure studies of NaH to 54 GPa. Phys. Rev. B, 36, 7664–7667. [CrossRef] [Google Scholar]
  5. Jain DC. 1963. Franck-Condon Factors and r-centroids for the Band System of the RbH Molecule. Proc. Phys. Soc., 81, 171–174. [CrossRef] [Google Scholar]
  6. Stwally WC, Zemke WT, Yang SC. 1991. Spectroscopy and structure of the alkali hydride diatomic molecules and their ions. J. Phys. Chem. Ref. Data, 20, 153. [NASA ADS] [CrossRef] [Google Scholar]
  7. Hooper J, Zurek E. 2012. Rubidium polyhydrides under pressure: emergence of the linear H3− species. Chem. A Eur. J., 18, 5013. [CrossRef] [Google Scholar]
  8. Zrafi W, Ovjia B, Berriche H, Gadea FX. 2006. Ab initio adiabatic and diabatic energies and dipole moments of the RbH molecule. J. Mol. Struct.: Theochem, 777, 87–97. [CrossRef] [Google Scholar]
  9. Ahuja R, Eriksson O, Johansson B. 1999. Theoretical search for the CrB-type high-pressure phase in LiH, NaH, KH and RbH. Physica B, 265, 87. [CrossRef] [Google Scholar]
  10. Fatmi M, Ghebouli B, Ghebouli MA, Bouhemadou A, Binanran S. 2012. Structural, electronic, optical and thermodynamic properties of NaxRb1−xH and NaxK1−xH alloys. J. Phys. Chem. Solids, 73, 1–7. [CrossRef] [Google Scholar]
  11. Hooper J, Baettig P, Zurek E. 2012. Pressure Induced Structural Transitions in KH, RbH and CsH. J. Appl. Phys., 111, 112611. [CrossRef] [Google Scholar]
  12. Sudba Priyanga G, Asuini Meenaatci AT, Rajeswara Palanichamy R, Iyakutti K. 2014. Structural, electronic and elastic properties of alkali hydrides (MH: M = Li, Na, K, Rb, Cs): Ab initio study. Comput. Mater. Sci., 84, 206–216. [CrossRef] [Google Scholar]
  13. Gonze X, Beuken JM, Caracas R, Detraux F, Fuchs M, Rignanese GM, Sindic L, Verstraete M, Zerah G, Jollet F, Torrent M, Roy A, Mikami M, Ghosez P, Raty JY, Allan DC. 2002. First-principles computation of material properties: the ABINIT software Project. Comput. Mater. Sci., 25, 478. [CrossRef] [Google Scholar]
  14. Blaha KSP, Madsen GKH, Kvasnicka D, Luitz J. 2001. An augmented plane wave + local orbitals program for calculating crystal properties, Universität Wien, Austria. [Google Scholar]
  15. Perdew JP, Burke K, Ernzerhof M. 1996. Generalized gradient approximation made simple. Phys. Rev. Lett., 77, 3865. [Google Scholar]
  16. Troullier N, Martins JL. 1991. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B, 43, 993. [CrossRef] [Google Scholar]
  17. Kohn W, Sham LJ. 1965. Self-consistent equations including exchange and correlation effects. Phys. Rev., 140, A1133. [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  18. Payne MC, Teter MP, Allan DC, Arias TA, Joannopoulos JD. 1992. Iterative minimization techniques for ab initio total-energy calculations: molecular dynamics and conjugate gradients. Rev. Mod. Phys., 64, 1045. [CrossRef] [Google Scholar]
  19. Monkhorst HJ, Pack JD. 1976. Special points for Brillouin-zone integrations. Phys. Rev. B, 13, 5188. [Google Scholar]
  20. Zinenko VI, Fedorov AS. 1994. First principle calculations of alkali hydride electronic structures. Sov. Phys. Solid State, 36, 742. [Google Scholar]
  21. Barrera GD, Colognesi D, Mitchell PCH, Ramirez Cuesta AJ. 2005. LDA or GGA? A combined experimental inelastic neutron scattering and ab initio lattice dynamics study of alkali metal hydrides. Chem. Phys., 317, 119. [CrossRef] [Google Scholar]
  22. Novakovic N, Radisavljevic I, Colognesi D, Ostojic S, Ivanovic N. 2007. First principle calculations of alkali hydride electronic structures. J. Phys. Condens. Matter, 19, 406211. [CrossRef] [Google Scholar]
  23. Sudha Priyanga G, Asvini Meenaatci AT, Rajeswara Palanichamy R, Iyakutti K. 2014. Structural, electronic and elastic properties of alkali hydrides (MH: M = Li, Na, K, Rb, Cs): Ab initio study. Comput. Mater. Sci., 84, 206. [CrossRef] [Google Scholar]
  24. Reshak H, Jamal M. 2012. DFT calculation for elastic constants of orthorhombic structure within WIEN2K code: A new package (ortho-elastic). J. Alloys Compd., 543, 147. [CrossRef] [Google Scholar]
  25. Engebretsen L. 1995. Electronic structure calculations of the elastic properties of alkali hydrides. Graduation Thesis, Royal institute of technology KTH, Stockholm. [Google Scholar]
  26. Zhang J, Zhang L, Lui T, Ma Y. 2007. Phonon and elastic instabilities in rocksalt alkali hydrides under pressure: First-principles study. Phys. Rev. B., 75, 104115. [CrossRef] [Google Scholar]
  27. Hochheimer HD, Strossner K, Honle W, Baranowski B, Filipek F. 1985. High pressure X-ray investigation of the alkali hydrides NaH, KH, RbH and CsH. Less J. Comm. Met., 107, L13. [CrossRef] [Google Scholar]

Cite this article as: Gulebaglan SE, Dogan EK, Secuk MN, Aycibin M, Erdinc B & Akkus H: First-principles study on electronic, optic, elastic, dynamicand thermodynamic properties of RbH compound. Int. J. Simul. Multisci. Des. Optim., 2015, 6, A6.

All Tables

Table 1.

Calculated lattice parameter a0 (Å) and energy gap Eg (eV).

In the text
Table 2.

Calculated elastic constants for RbH with NaCl structure.

In the text
Table 3.

Calculated single crystal bulk modulus (B0), Young modulus (E), shear modulus (G), anisotropy factor (A), Poisson’s ratio (ν) obtained for RbH.

In the text
Table 4.

The calculated phonon frequencies at Γ, X and L points for RbH.

In the text

All Figures

thumbnail Figure 1.

Plotted electronic band structure for RbH.
In the text
thumbnail Figure 2.

Real and imaginary parts of dielectric function for RbH.
In the text
thumbnail Figure 3.

Calculated (a) reflectivity spectrum (R), (b) absorption (α) coefficient and (c) extinction coefficient (k) for RbH.
In the text
thumbnail Figure 4.

The calculated spectral dependence of refractive index (n) on wavelength of RbH.
In the text
thumbnail Figure 5.

Volume and surface loss functions (L) for RbH as a function of photon energy for RbAu.
In the text
thumbnail Figure 6.

Phonon dispersion curves and phonon density of states for RbH.
In the text
thumbnail Figure 7.

(a) Phonon contribution to the free energy as a function of temperature, (b) phonon contribution to the internal energy, (c) the entropy as a function of temperature and (d) constant volume specific heat as a function of temperature, as a function of temperature for RbAu.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.