| Issue |
Int. J. Simul. Multidisci. Des. Optim.
Volume 12, 2021
Computation Challenges for engineering problems
|
|
|---|---|---|
| Article Number | 18 | |
| Number of page(s) | 8 | |
| DOI | https://doi.org/10.1051/smdo/2021017 | |
| Published online | 26 August 2021 | |
Research Article
Free vibration and inherent material damping characteristics of boron-FRP plate: influence of non-uniform uniaxial edge loads
1
Department of Mechanical Engineering National Institute of Technology Karnataka Surathkal, Mangalore 575 025, India
2
School of Mechanical and Building Sciences VIT University, chennai, Tamilnadu 600 127, India
* e-mail: yajiv062@gmail.com
Received:
7
January
2021
Accepted:
29
June
2021
The current investigation presents the analytical investigation on free vibration and inherent material damping of boron-FRP plate, subjected to non-uniform uniaxial edge loads. Initially critical buckling load (Pcr) is obtained, then followed by free vibration response and inherent material damping values for corresponding modal indices of the FRP plate is calculated for different load fraction of non-uniform uniaxial edge loads. The buckling load and free vibration response are obtained by using strain energy method and Reddy's TSDT respectively. It is observed that the nature of load and aspect ratio influence the bucking, free vibration and inherent material damping behaviour of the fibre reinforced polymer plate significantly.
Key words: Analytical solutions / non-uniform in-plane loads / Reddy's TSDT / inherent damping
© V. Gunasekaran et al., Published by EDP Sciences, 2021
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Fiber-reinforced plastic (FRP) composites plate made up of born-epoxy, are extensively used in automobile, aerospace, naval, and other engineering applications due to their tailoring properties for a less weight to high stiffness. For the better dynamic design consideration, henceforth damping and buckling studies of the engineering structures are considered to be an imperative factor. Due to boron-fiber and epoxy-matrix interactions (i.e., acting like viscoelastic material) compared to the traditional materials, these boron-FRP structures have inherent material damping. During the working condition, these born-FRP structures exposed to non-uniform uniaxial edge (NUE) loads. Which varies the stiffness of the structure and cause change in free vibration and inherent material damping behavior. So, it is important to monitor the free vibration and inherent material damping behavior of boron-FRP plate subjected to different NUE loads. Timoshenko and Gere [1] analyzed the buckling behavior of flat isotropic simply supported structure by obtaining equilibrium governing differential equation, to predict an accurate buckling load of the structure. Reddy [2] analytically derived various shear deformation theories to study the dynamic characteristics of the structure subjected to the different boundary conditions and external arbitrary forces. Kang and Leissa [3] have benchmarked the analytical method for calculating the accurate buckling load of a metal plate under the fluctuating in-plane edge load, by using a fourth-order partial differential equation. Mijuskovic et al. [4] theoretically studied the instability of flat plate subjected to the arbitrary edge loads under varied boundary conditions with the help of the Ritz energy method. Ferreira et al. [5] derived an analytical formulation for laminated plates to predict the accurate buckling load and its mode, by using a radial basis function on Reddy's TSDT. Stoodeh and Karami [6] employed the numerical method to calculate the vibration and buckling characteristics of anisotropic composite plates, with the help of layer-wise FEM. Bhagat et al. [7] used finite element analysis to study the vibration and instability characteristics of flat metal structure exposed to the non-uniform thermal load. Khdeir and Librescu [8] theoretically examined the instability and vibration characteristics of cross-ply composite, based on higher-order plate theory combined with the state-space concept. Dickinson [9] inspected a profound analytical approach to determine vibration and instability characteristics of orthotropic flat plate, with the help of Warburton equation for the various boundary conditions.
Sayyad et al. [10–12] has done the detailed analytical study of buckling and vibration on anti-symmetric laminated plates by using novel trigonometric theory which includes shear deformation effect, to understand the effects of slender ratio, modular ratio and fibre angle of the composite plate. Ferreira et al. [13] numerically analysed the vibration and instability of composite plates under irregular geometries by considering the radial basis function on FSDT. Gunasekaran et al. [14] investigated analytically the variations in vibration frequencies of FG-graphene reinforced plates under arbitrary edge loads. Arunkumar et al. [15] numerically studied the bending and dynamic characteristics of the foam-filled sandwich panel by using FEM. Kumar et al. [16] have benchmarked a numerical solution for the vibration response of laminated plates, with the help of 2D FE model incorporated with a higher-order zigzag theory which is considered interlaminar shear stress. Alam and Asnani [17] used the variational principle to predict the dynamic and damping factor of fibre-reinforced plastic plates subjected to simply supported boundary conditions. Chandra et al. [18] given a brief literature review about a damping study in fiber-reinforced composite materials by using micromechanical, micromechanical, and viscoelastic methods. Sudhakar et al. [19] done a detailed investigation of rotating tapered laminates on frequencies and its damping factors, with the help of FEM based on the FSDT. Arunkumar et al. [20] done a detailed numerically investigated the acoustic radiation behaviour of sandwich panel by considering the inherent material damping. Jeyaraj et al. [21] presented the numerical study of acoustic radiation characteristics of the FRP structure under the thermal load by considering inherent material damping by following a combined FEM/BEM approach. Gunasekaran et al. [22] theoretically investigation the influence of arbitrary loads on the sound radiation behaviour of simply supported isotropic plate, with the help of strain energy and TSDT approach. Xiang et al. [23] used nth order shear deformation theory to analyse the free vibration behaviour of laminated composite plates.
In most of the practical cases the FRP structures are subjected to NUE stresses loads. Examples are local instability of stiffener, walls, floor and skin panels of wings of an aircraft are widely made up of FRP structures. During the on-flight conditions, these structures experience normal compression with uniform pressure. Due to this the panel edges are subjected to combined tensile and compressive stresses. So, it is important to investigate effect of NUE loadings on buckling and free vibration characteristics of a FRP structure.
Form the above detailed literature evaluation, it is concluded that the investigation of inherent material damping and free vibration characteristics of the fibre reinforced polymer laminated plate under different NUE loads is still an unexplored region of research. Present paper, mandates analytical investigation on the effects of non-uniform in-plane edge loads on the inherent material damping and natural frequencies of boron fibre reinforced polymer laminate.
2 Methodology
All side simply supported boron-FRP plate, under the non-uniform uniaxial in-plane load considered for the present study is shown in Figure 1. With the help of Strain energy approach, the buckling strength of boron-FRP plate is predicted analytically. By using Reddy's third order shear deformation theory (TSDT) approach, dynamic response of boron-FRP plate is obtained, to understand the variation in natural frequencies and inherent material damping. Equation (1) represents the common load intensity formulation of different NUE loads. To obtain the buckling load value (Pcr) of boron-FRP under NUE loads, the main characteristic equation (Eq. (2)) is solved by using second order approximation for Alpha (α) is 0, 1 and 1.5 and third order approximation for Alpha (α) is 2 case. For the free vibration analysis and material inherent damping of the FRP plate is obtained by solving equations (3) and (4) by considering Reddy's TSDT approach, the reader is referred to Reddy [2] and Jeyaraj et al. [21] for more details of the derivation.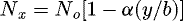 (1)
(1)
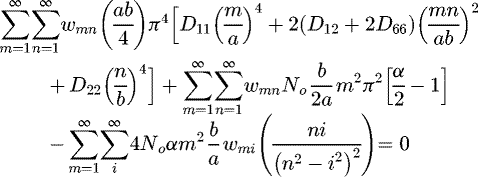 (2)
(2)
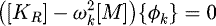 (3)
(3)
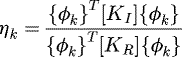 (4)where D11, D12, D66 and D22 are boron-FRP plates bending stiffness components.m is buckling mode number of x axis direction, whereas n is in y axis direction of boron-FRP plate.
(4)where D11, D12, D66 and D22 are boron-FRP plates bending stiffness components.m is buckling mode number of x axis direction, whereas n is in y axis direction of boron-FRP plate. 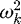 is circular natural frequency and φk is respective mode shape, ηk is modal loss factor, ω is exciting frequency, [M] mass matrix, [K] is stiffness matrix where suffix R and I denotes the real and imaginary.
is circular natural frequency and φk is respective mode shape, ηk is modal loss factor, ω is exciting frequency, [M] mass matrix, [K] is stiffness matrix where suffix R and I denotes the real and imaginary.
 |
Fig. 1 FRP plate subjected to non-uniform edge loads. |
3 Validation studies
3.1 Buckling load
All side simply supported metal plate, under the NUE loads studied by Kang and Lessia [3] is chosen for the buckling characteristic validation. Kang and Lessia [3] used minimum buckling load 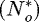 to characterize the buckling strength of the plate under different NUE loads. Buckling load value calculated by current method shows a upright agreement with Kang and Lessia [3] which is shown in Table 1. The minimum buckling load
to characterize the buckling strength of the plate under different NUE loads. Buckling load value calculated by current method shows a upright agreement with Kang and Lessia [3] which is shown in Table 1. The minimum buckling load 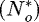 is given as
is given as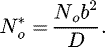 (5)
(5)
3.2 Free vibration and damping
Since there are no clear study has been found in inherent damping characteristics of simply supported FRP plate, based on finite element approach of commercial software ANSYS is used for the validation of the present analytical method. A single layer boron-FRP with the dimension (1 × 1 × 0.001 m3) is used for validation of free vibration and inherent damping of boron-FRP plate. It is found that calculated complex natural frequency and inherent material damping of present analytical method is closely matching with ANSYS results which is shown in Table 2.
Comparison of complex natural frequency and damping with ANSYS.
4 Results and Discussions
In this study cross-ply (0/90/0/90/0/90)s and angle-ply (− 45/45/− 45/45/− 45/45)s laminates made of boron-epoxy are considered, assumed that all edges are simply supported. The plate considered has a layer thickness of 0.16 mm and investigated for three aspect ratios (a/b) of 0.5, 1.25 and 2 with the constant slenderness ratio (b/h) as 200 by maintaining constant value of b = 0.4 m. The FRP plate has the properties of boron fibre reinforced polymer (BFRP) which is given as complex value for predicting the inherent material damping, where E1 = 211(1+0.0014j) GPa, E2 = 21.1(1+0.0008j) GPa, G12 = G13 = 7(1+ 0.011j) GPa, ν = 0.3 and ρ = 1882 kg/m3. The present investigations, dimensionless natural frequency and buckling load as given in equations (6) and (7)).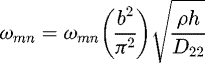 (6)
(6)
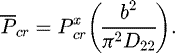 (7)
(7)
4.1 Buckling response
In this section, the impact of NUE loads on the dimensionless buckling load of simply supported boron-FRP plates is detailly investigated. Buckling load ratio (BLR) and dimensionless buckling load of boron-FRP plate subjected to different NUE loads are shown in Table 3. It is observed that the aspect ratio (a/b) and different load configuration of NUE loads have a significant impact on the buckling behavior of boron-FRP plates. As the plate aspect ratio (a/b) rises, the buckling mode number (m) in the x-direction in which the plate buckles increase and simultaneously reduces the dimensionless buckling load value. With constant one buckling mode number (n) in the y-direction of the plate. It is also noted from Table 3, that dimensionless buckling load increase as rise in load factor (α) value. Due to increase in asymmetricity of load configuration and the tensile force effect of NUE loads as load factor (α) rises. An upsurge in load factor (α), provides extra stiffness of the boron-FRP plates, when compared to the benchmark uniform distributed load case (i.e., α = 0). Hence the boron-FRP plate attains more stability and buckles at the higher dimensionless buckling load value. Angle-ply boron-FRP plates provide high buckling strength, due to its own inherent elastic properties and lay-up orientation as results in high plate cross-sectional rotary inertia value which provide higher bending and transverse shear stiffness for the plate compared to the cross-ply boron-FRP plates. In load factor α = 2 case, the stability of boron-FRP plate enhanced due to the higher load intensity area of tensile force and attains maximum value of dimensionless buckling load value then the remaining load factor (α) cases. By using Reddy's TSDT approach the free vibration response of boron-FRP plate is obtained by using buckling load ratio (BLR) which is given in Table 3.
Effect of NUE load on dimensional buckling load.
4.2 Dynamic response
In this section, the variation of dimensionless natural frequencies with a rise in different NUE loads is shown in Figure 2. When boron-FRP plates are exposed to the corresponding NUE buckling load, the dimensionless natural frequencies of the fundamental mode approaches zero. It is also noted that it is impossible to attain higher buckling mode, for the NUE loads exposed at the shorter length of the plate. Due to this the boron-FRP buckles with (1,1) mode for all load cases when aspect ratio is 0.5. However, load factor cases α = (0,1) and α = (1.5,2) of the boron-FRP plate buckles at (1,1) and (2,1) mode for aspect ratio is 1.25, due to its own material inherent orientation properties and larger length of the plate exposed to the NUE loads. Whereas the boron-FRP plate buckles (2,1) for load factor case α = (0, 1, 1.5) and (3,1) mode for α = 2 case, when aspect ratio is 2. Form Figure 2., it is clearly noted that when the aspect ratio rises above one by default the buckling mode number for α = 2 will be higher when associated to rest of the cases, due to tensile force it obtains the more stability to buckle at higher mode.
Table 4 shows the impact of different NUE loads on the representation of modal loss factors (i.e., inherent material damping) associated with its dimensionless natural frequencies. As the free vibration analysis is done by increasing load fraction of buckling load for the respective boron-FRP plates, it is evident that reduce of frequency mode towards zero. But the modal loss factor values increase to a very high value, which causes diminished of the frequency mode at the full fraction of buckling load acting on the boron-FRP plates. This is due to the reducing stiffness effect caused by the NUE loads. For better understanding, the graphical representation of the effect of different NUE loads on the dimensional natural frequencies and inherent material damping is shown in Figure 3, with the constant aspect ratio (a/b = 1.25) is chosen for cross-ply and angle-ply boron-FRP plates. Figure 4. shows the effect of NUE load α = 2 cases on the free vibration mode shapes, it is clearly shown that rise in buckling load fraction. The boron-FRP plate buckles at (2,1) mode instead of (1,1) mode and observed that shift of mode shape towards the lower region due to the tensile forces acting at the top region of the boron-FRP plate.
 |
Fig. 2 Effect of NUE loads on dimensional buckling load. (a) Cross ply, (a/b) = 0.5. (b) Angle ply, (a/b) = 1.25. (c) Cross ply, (a/b) = 2. (d) Angle ply, (a/b) = 2. |
Effect of NUE loads on dimensional natural frequencies and inherent material damping (a/b = 1.25).
 |
Fig. 3 Effect of NUE loads on dimensional natural frequencies and inherent material damping. (a) Cross ply, (a/b) = 1.25. (b) Angle ply, (a/b) = 1.25. (c) Cross ply, (a/b) = 1.25. (d) Angle ply, (a/b) = 1.25. (e) Cross ply, (a/b) = 1.25. (f) Angle ply, (a/b) = 1.25. |
 |
Fig. 4 Effect of NUE loads on free vibration modes. |
5 Conclusions
Strain energy approach is employed to determine the dimensionless buckling load, free vibration response of BFRP plate is obtained by using Reddy [2] TDST approach. It's observed that non-uniform edge load has signification effect on the dimensionless natural frequency and inherent material damping of the boron-FRP plate. Fundamental buckling mode for load case alpha = 2 always obtain the higher buckling mode, when compared to the other load cases. Shifting of modal frequencies are observed in the load case alpha = 2 and when the boron-FRP plate has higher aspect ratio (a/b). A very high rise in the modal loss factor (i.e., inherent damping values for the respective modal indices) is observed in the fundamental natural frequency of the boron-FRP plate when the load fraction is 0.975 Pcr for the corresponding non-uniform load cases.
References
- S.P. Timoshenko, J.M. Gere, Theory of elastic stability (Courier Corporation, 2009) [Google Scholar]
- J.N. Reddy, Mechanics of laminated composite plates and shells: theory and analysis (CRC Press, 2003) [Google Scholar]
- J.-H. Kang, A.W. Leissa, Exact solutions for the buckling of rectangular plates having linearly varying in-plane loading on two opposite simply supported edges, Int. J. Solids Struct. 42, 4220–4238 (2005) [CrossRef] [Google Scholar]
- O. Mijušković, B. Ćorić, B. Šćepanović, Exact stress functions implementation in stability analysis of plates with different boundary conditions under uniaxial and biaxial compression, Thin-Walled Struct. 80, 192–206 (2014) [Google Scholar]
- A. Ferreira, C. Roque, A. Neves, R. Jorge, C.M. Soares, J. Reddy, Buckling analysis of isotropic and laminated plates by radial basis functions according to a higher-order shear deformation theory, Thin-Walled Struct. 49, 804–811 (2011) [Google Scholar]
- A. Setoodeh, G. Karami, Static, free vibration and buckling analysis of anisotropic thick laminated composite plates on distributed and point elastic supports using a 3-d layer-wise fem, Eng. Struct. 26, 211–220 (2004) [CrossRef] [Google Scholar]
- V.S. Bhagata, J. Pitchaimani, S. Murigendrappa, Buckling and vibration behavior of a non-uniformly heated isotropic cylindrical panel, Struct. Eng. Mech. 57, 543–567 (2016) [Google Scholar]
- A. Khdeir, L. Librescu, Analysis of symmetric cross-ply laminated elastic plates using a higher-order theory: Part II-buckling and free vibration, Compos. Struct. 9, 259–277 (1988) [Google Scholar]
- S. Dickinson, The buckling and frequency of flexural vibration of rectangular isotropic and orthotropic plates using rayleigh's method, J. Sound Vib. 61, 1–8 (1978) [Google Scholar]
- A.S. Sayyad, Y.M. Ghugal, On the buckling of isotropic, transversely isotropic and laminated composite rectangular plates, Int. J. Struct. Stab. Dyn. 14, 1450020 (2014) [Google Scholar]
- A.S. Sayyad, Y.M. Ghugal, On the free vibration of angle-ply laminated composite and soft core sandwich plates, J. Sandwich Struct. Mater. 19, 679–711 (2017) [Google Scholar]
- A.S. Sayyad, B.M. Shinde, Y.M. Ghugal, Bending, vibration and buckling of laminated composite plates using a simple four variable plate theory, Latin Am. J. Solids Struct. 13, 516–535 (2016) [Google Scholar]
- A. Ferreira, C. Roque, A. Neves, R. Jorge, C. Soares, K.M. Liew, Buckling and vibration analysis of isotropic and laminated plates by radial basis functions, Compos. Part B 42, 592–606 (2011) [Google Scholar]
- V. Gunasekaran, J. Pitchaimani, L.B.M. Chinnapandi, Analytical investigation on free vibration frequencies of polymer nano composite plate: effect of graphene grading and non-uniform edge loading, Mater. Today Commun. 24, 100910 (2020) [Google Scholar]
- M. Arunkumar, J. Pitchaimani, K. Gangadharan, Bending and free vibration analysis of foam-filled truss core sandwich panel, J. Sandwich Struct. Mater. 20, 617–638 (2018) [Google Scholar]
- A. Kumar, A. Chakrabarti, P. Bhargava, Vibration of laminated composites and sandwich shells based on higher order zigzag theory, Eng. Struct. 56, 880–888 (2013) [Google Scholar]
- N. Alam, N. Asnani, Vibration and damping analysis of fibre reinforced composite material plates, J. Compos. Mater. 20, 2–18 (1986) [Google Scholar]
- R. Chandra, S. Singh, K. Gupta, Damping studies in fiber-reinforced composites − a review, Compos. Struct. 46, 41–51 (1999) [CrossRef] [Google Scholar]
- P.E. Sudhagar, A.A. Babu, V. Rajamohan, P. Jeyaraj, Structural optimization of rotating tapered laminated thick composite plates with ply drop-offs, Int. J. Mech. Mater. Des. 13, 85–124 (2017) [Google Scholar]
- M. Arunkumar, M. Jagadeesh, J. Pitchaimani, K. Gangadharan, M.L. Babu, Sound radiation and transmission loss characteristics of a honeycomb sandwich panel with composite facings: effect of inherent material damping, J. Sound Vib. 383, 221–232 (2016) [Google Scholar]
- P. Jeyaraj, N. Ganesan, C. Padmanabhan, Vibration and acoustic response of a composite plate with inherent material damping in a thermal environment, J. Sound Vibr. 320, 322–338 (2009) [CrossRef] [Google Scholar]
- V. Gunasekaran, J. Pitchaimani, L.B.M. Chinnapandi, Vibro-acoustics response of an isotropic plate under non-uniform edge loading: an analytical investigation, Aerospace Sci. Technol. 105, 106052 (2020) [Google Scholar]
- S. Xiang, S.X. Jiang, Z.Y. Bi, Y.X. Jin, M.X. Yang, A nth-order meshless generalization of reddy's third-order shear deformation theory for the free vibration on laminated composite plates, Compos. Struct. 93, 299–307 (2011) [Google Scholar]
Cite this article as: Vijay Gunasekaran, Pitchaimani Jeyaraj, Lenin Babu Mailan Chinnapandi, Free vibration and inherent material damping characteristics of boron-FRP plate: influence of non-uniform uniaxial edge loads, Int. J. Simul. Multidisci. Des. Optim. 12, 18 (2021)
All Tables
Effect of NUE loads on dimensional natural frequencies and inherent material damping (a/b = 1.25).
All Figures
 |
Fig. 1 FRP plate subjected to non-uniform edge loads. |
| In the text | |
 |
Fig. 2 Effect of NUE loads on dimensional buckling load. (a) Cross ply, (a/b) = 0.5. (b) Angle ply, (a/b) = 1.25. (c) Cross ply, (a/b) = 2. (d) Angle ply, (a/b) = 2. |
| In the text | |
 |
Fig. 3 Effect of NUE loads on dimensional natural frequencies and inherent material damping. (a) Cross ply, (a/b) = 1.25. (b) Angle ply, (a/b) = 1.25. (c) Cross ply, (a/b) = 1.25. (d) Angle ply, (a/b) = 1.25. (e) Cross ply, (a/b) = 1.25. (f) Angle ply, (a/b) = 1.25. |
| In the text | |
 |
Fig. 4 Effect of NUE loads on free vibration modes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




