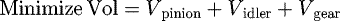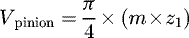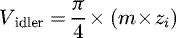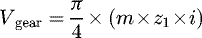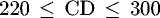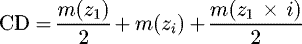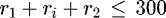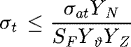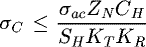| Issue |
Int. J. Simul. Multidisci. Des. Optim.
Volume 10, 2019
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 11 | |
| DOI | https://doi.org/10.1051/smdo/2019009 | |
| Published online | 16 April 2019 | |
Research Article
Design optimization of a three-stage transmission using advanced optimization techniques
1
Department of Industrial and Manufacturing Engineering, Harare Institute of Technology, Belvedere, Harare, Zimbabwe
2
Department of Mechanical Engineering, Amity University Haryana, Gurgaon 122413, India
* email: esmaputi@gmail.com
Received:
28
February
2019
Accepted:
26
March
2019
Gear transmission systems are very important machine elements and their failure can lead to losses or damage of other mechanical components that comprise a machine or device. Since gears are applied in numerous mechanical devices, there is need to design and subsequently optimize them for intended use. In the present work, two objectives, viz., volume and center distance, are minimized for a rotary tiller to achieve a compact design. Two methods were applied: (1) analytical method, (2) a concatenation of the bounded objective function method and teaching–learning-based optimization techniques, thereby improving the result by 44% for the former and 55% for the latter. Using a geometric model and previous literature, the optimal results obtained were validated with 0.01 variation. The influence of design variables on the objective functions was also evaluated using variation studies reflecting on a ranking according to objective. Bending stress variation of 12.4% was less than contact stress at 51% for a defined stress range.
Key words: Gear / optimal design / design preferences / optimization
© E.S. Maputi and R. Arora, published by EDP Sciences, 2019
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Mechanization is a key economic enabler for improved product volumes and efficiency in industrial and agricultural production systems. Gears are key mechanical elements that enable the transmission of power in differing configurations and output ranges. Their application in agricultural, automotive, manufacturing, power generation, aerospace, and marine industries further demonstrates the potential for improvement that could be realized through optimization studies. The optimization of gear systems has been extensively investigated and the literature surveyed identifies the application of computational methods as early as the 1970s [1–3].
With the improvement of optimization theory and introduction of new methods and tools such as advanced and evolutionary algorithms [4,5], researchers have also applied these to gear optimization [6–8]. However, literature shows that various methodology based on decision practice and computer-aided argumentations [9–11] have been applied to the study of gear systems. Gear systems can be classified according to the type or constructional arrangement: the latter being a broad classification, while the former is specific. Furthermore, gear arrangement can be defined by axes, whether they are parallel or perpendicular, or by the number of stages forming a gear system. Gear types such as worm and wheel, spur, bevel, and helical have been investigated by researchers [12–14] while using various optimization methods. Single-stage, multistage, and multispeed gear systems have been investigated in literature [15,16] while considering numerous gear types.
The consideration of multiple objectives is necessary since gears by nature are defined by numerous parameters that may singularly/simultaneously require maximization and minimization. Multiobjective optimization may be applied using three different methodologies, viz., a priori, a posteriori, and progressive articulation [16]. A priori articulation informs the optimization process with designer preferences by via weights as espoused in weighted sum, e-constraint, and weighted metric methods. Such methodology does not result in a general Pareto frontier but rather one that is biased toward the designer's intent. While applying an a priori method, Stefanović-Marinović et al. [17] applied a weighted coefficients method to four objectives for optimization on a planetary gear system. Other researchers argue that the criteria for setting weights need to be informed by sensitivity analysis.
A posteriori articulation method begins with the generation of a Pareto frontier that is then investigated using decision methods such as Linear Programming for Multidimensional Analysis of Preference (LINMAP), Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), and Fuzzy [18,19] in order to identify the optimal result. This allows for trade-off studies [15] to be performed on the frontier to discover new insights on objectives, variable, and constraint assignments. Progressive articulation allows the preferences weights or factors to be adjusted as the optimization process is running.
Numerous optimization techniques have been applied to gear design problems, viz., particle swarm optimization, genetic algorithm, simulated annealing, sheep flock algorithm, teaching–learning-based algorithms, etc. Researchers have made comparisons on convergence rate, time to solution, and the optimal result while searching for better algorithm applications. In all these investigations, numerous combinations of objectives, viz., volume, efficiency, power output, center distance, mass, and cost were considered.
Literature surveyed indicates the following:
-
That most gear design problems investigated are abstract in formulation and presumed to apply on numerous applications.
-
The application of gears under investigation has not been included in setting designer preferences
-
Application of advanced optimization techniques in gear optimization has not been investigated.
In the present work, a three gear-train design problem that was investigated by Akinci et al. [20] for gear failure is further considered for optimization. The minimization of center distance and volume informs of a compact configuration that reduces material cost and energy usage. In the presented research work, Section 2 describes a rotary tiller, its functions, and the setup of the gear transmission system. Section 3 reflects on gear design methodology with a focus on the AGMA design procedure that is applied analytically.
Section 4 discusses the engineering design optimization and highlights the boundary objective function (BOF) and teaching–learning-based optimization (TLBO) methods. Section 5 introduces the design problem as a mathematical formulation. Results of the optimization process are shown in Section 6 with variation and validation studies, while Section 7 is the conclusion of research work.
2 System description
Rotary cultivators are not simply tractor-drawn implements but are also powered through the power takeoff (PTO) shaft of a tractor. The implement is mounted at the rear end of a tractor while supported by a linkage system [20]. The power transmission mechanism of a rotary cultivator, shown in Figure 1, is composed of a bevel gear unit that is linked to a three-gear train system composed of spur gears. The three-gear train system is composed of two gears that mesh with an idler gear. Power is transmitted from the PTO point and passes through a bevel gear arrangement. The output of this first gear system is generated at an angle of 90° to connect with the second gear unit. The second gear unit through a parallel shaft arrangement then transmits the power to the tiller unit that is composed of spade knives.
Spur gears in general are geometrically cylindrical and mesh with each other to form gear stages. The system under investigation can be described as single stage with an idler or rather as a three-gear two-stage system. The specifications for rotary tiller gear train system are recorded in Table 1.
 |
Fig. 1 Rotary tiller gear train system. |
3 Gear design
Researchers and industry practitioners have advanced gear design practice over numerous years by applying state-of-the-art computational tools to previously known manual procedures. The gear design process is iterative and involves numerous variables and constraints that increase the cost of computation. The direct gear design method was introduced by Kapelevich [21] as an attempt to formalize the design process, while other researchers introduced novel, practical, and computer-aided methods [10,11,22]. Fundamentally, gear design procedures emanate from geometric relations of parameters such as module, gear tooth number, and face width. Parameter sets are then evaluated for bending and surface/contact stress. Generally, the bending stress calculation emanates from the Lewis equation that analyzes the gear tooth as a beam under load, while surface fatigue is derived from hertz contact stress analysis. Failure in gear operation occurs mainly due to contact/surface and bending stress.
The balance in favor of either stress factor depends on the application, selection, and computation of safety factors. Gear transmission systems are key to the industrial systems such that design standards have been instituted to aid the practice. Numerous gear design standards exist for various types of gears and applications and in this research, the American Gear Manufacturers Association standard (AGMA 2001-D04) “Fundamental Rating Factors and Calculation Methods for Involute Spur and Helical Gear Teeth” is applied.
3.1 AGMA design procedure
The acronym AGMA refers to the America Gear Manufacturers Association that has developed numerous standards for gear design. In this research the AGMA standard (AGMA 2001-D04) that is specific to spur and helical gears is utilized. Figure 2 shows the design procedure as implemented in this research work. A defined set of input data is required to initialize the design process. These data are used in the preliminary design phase, before calculation of the bending and contact stress values. This preliminary phase seeks to interpret the input parameters for the transmission system.
This is essentially a load analysis phase to determine the effects of input power as expressed by equations (1)–(5).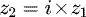 (1)
(1)
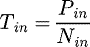 (2)
(2)
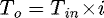 (3)
(3)
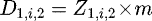 (4)
(4)
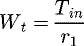 (5)
(5)
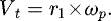 (6)
(6)
After this preliminary stage, the bending stress analysis begins with estimation of face-width value and setting of the following factors: km
, kv
, ks
, kb
, kt
, kr
, I, and J. The bending stress value is then evaluated according to equation (7). The material to be used for manufacturing the gear has been selected prior to computation and its hardness value is used to estimate the allowable bending stress by use of equation (8). Similarly, contact stress and allowable contact stress are evaluated using equations (9) and (10). (7)
(7)
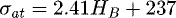 (8)
(8)
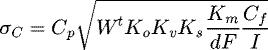 (9)
(9)
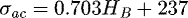 (10)
(10)
 (11)
(11)
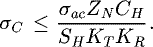 (12)
(12)
The calculated stress values must always be lower than the allowable stress values and the ratio of these values is the safety factor of the design. Safety factors depend on application and are usually set by the designer. As shown in Figure 2, if the stress factor is not satisfactory, the design procedure loops back to the first stage to begin the second iteration until a suitable solution is reached.
 |
Fig. 2 AGMA design procedure for spur and helical gears. |
3.2 Engineering design optimization
Traditional design procedures map the decision process from need through prototyping to final product [23]. Design procedures can also be classified into phases or stages such as preliminary and detailed design.
The former defines the initial stages of the design where a priori articulation is done based on experience/or by the use of a decision-based method. The detailed design phase then articulates the finer details of the chosen design that are based on the preferences set by the designer. Resultantly, final results can be sufficient but not optimal due to subjectivity in setting preferences. Design may be defined as a goal-seeking activity within a defined solution space.
In other words, design is a search process instructed by an objective, boundary metrics, and constraints, which represent a problem definition. Such definitions are the rudder of the search process and their formulation impacts the rate of convergence to a solution and the certainty of optimality. Literature [24–26] shows that there is increasing application of computing and optimization algorithms to solve design engineering and scientific problems. Such investigations have resulted in discovery of new optimal values while using less resources and time.
Generally, optimization is performed to either minimize/maximize an objective. However, optimization processes are influenced by numerous factors. Objectives may be singular (single objective) or multiple (multiobjective). Constrained optimization is whereby the max/min of an objective is investigated subject to defined constraints on the objective. In gear design, bending, surface fatigue limits and interference checks are some of the constraints to be considered. Furthermore, the numeric size of shafts, bearings, materials, and parts is not available in continuous but integer form. In this research work, center distance and volume objectives are minimized by formulating a scalarized objective function.
4 Optimization
Broadly, optimization may be classified as either single-objective or multiobjective optimization, with the latter defined as the simultaneous and systematic process by which objectives are optimized. When more than one objective is investigated, change in one objective will impact the corresponding objectives. When two objectives are considered, a Pareto frontier [18] is obtained.
The Pareto frontier is a set of optimal solution sets that can be obtained for a given multiobjective problem. On this frontier, trade-off studies can be performed to ascertain the impact of variable changes. On the other hand, multiple objectives may not be of equal importance with regard to the ultimate goal sought by the designer. In view of this, methods to prioritize objectives may be employed by setting weights as preference values. In recent years, various multiobjective optimization studies have been carried out by a number of researchers [27–35].
The articulation of preferences may be done a priori, progressively, or a posteriori to the optimization exercise. A priori articulation refers to the setting of design preferences before the optimization process such that they are included in the objective functions. Essentially, multiobjective processes can be classified into two approaches: vector and scalarization methods [36]. Vector methods refer to the sequentially independent optimization of each objective function depending on a set of preferences. On the other hand, scalarization results in a single function that is then applied to a single-objective methodology.
4.1 Weighted sum method (WSM)
This is a very common method that applies weights to objective functions as measure or indicator of importance and can be described mathematically as follows: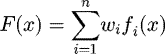 (13)
where w represents a vector of weights that sum up to 1, with values in the range of 0–1. These weights can be applied a priori or a posteriori to problem solving where in the latter case weights are varied to obtain different optimal results. This method is relatively easy to use and for weights in the range prescribed earlier, Pareto optimality can be achieved. However, major challenges arise from weight assignment and the certainty of true optimality based on systematic variation of weights.
(13)
where w represents a vector of weights that sum up to 1, with values in the range of 0–1. These weights can be applied a priori or a posteriori to problem solving where in the latter case weights are varied to obtain different optimal results. This method is relatively easy to use and for weights in the range prescribed earlier, Pareto optimality can be achieved. However, major challenges arise from weight assignment and the certainty of true optimality based on systematic variation of weights.
4.2 Weighted min–max method (WMM)
This method unlike the weighted sum can provide all Pareto and non-Pareto points. It is, however, computationally expensive, requires setting of more constraints, and has ambiguity in single-solution point problem and weight settings. Also referred to as the weighted Tchebycheff method, mathematically it may be described as follows:
Considering a function F(x), (14)
(14)
This may be modified by introducing a parameter λ:
Minimize λ
Subject to (15)where i = 1 to k
(15)where i = 1 to k
4.3 Weighted global criterion (WGC)
Another multiobjective optimization method is WGC. This is a type of scalarization method whose parameters are not directly related to preferences. Mathematically, it may be defined as follows: (16)
(16)
The parameters p and w are not varied simultaneously, rather p is selected and then a predetermined weight based on preferences is applied as w. Various values of p such as 1,2, and ∞ result in WSM, compromise, and the WMM, respectively.
4.4 Lexicographic method (LM)
This is classified as a vector multiobjective optimization method whose preferences are reflected by the order of optimization [36]. Pareto optimal solution is guaranteed with its unique way of specifying preferences. However, it is computationally expensive since it is effective with a global optimization tool. The goal programming (GP) method applies goals to each objective and strives to minimize the total deviation of all the goals. There is no guarantee of reaching an optimal solution, with an increase in variables and constraints that make the method undesirable.
4.5 Bounded objective function (BOF) method
This method focuses on the single most important objective while treating all other objectives as constraints. A variant of this method is the e-constraint method [23]. When applying this method, it is not necessary to normalize the objective functions and it guarantees an optimal solution when one exists. As per definition, it focuses on a single objective as selected by the designer. Essentially, this method reduces the multiobjective problem into a single-objective formulation.
4.6 Advanced optimization techniques
Optimization techniques are multidisciplinary tools, hence this has sparked research and development of many new techniques and hybridization of those existing. Two major advantages that advanced techniques possess over classical are hybrid ability and universality. Nature-inspired/evolutionary techniques are those based on study of the behavior of nature (animals and plants) and are also classified as advanced optimization techniques. Such techniques include artificial bee colony (ABC), genetic algorithms (GAs), differential evolution (DE), harmony search (HS), artificial immune algorithms (AIA), bacteria foraging optimization (BFO), particle swarm optimization (PSO), and shuffled frog leaping (SFL). With regard to gear design optimization, techniques such as PSO, SA, and GA have been widely applied in single-objective optimization problems.
In this research work, a three-gear train system is optimized using the TLBO algorithm.
Philosophically, the TLBO algorithm is derived from the relations between an educator, students, and their peers in a learning environment. In this environment, basically two activities occur, namely, teaching (teacher stage) and learning (learner stage). Interaction between student and teacher results in knowledge enrichment as the teacher is considered as the ideal. Further interaction between high-performing students and their peers results in improvement of the peers.
As is synonymous with pedagogy, subjects are pursued and evaluated at the end of a course to measure improvement. Rao [37] linked these concepts with the mathematical formulation of an optimization problem. The students in the class are considered the population, variables (design parameters) representing subjects, while the fitness function (objective function) is reflected by the evaluation of subject marks.
4.6.1 Teacher phase
As shown in Figure 3, the teaching phase begins after initialization. The mean is calculated and solutions ranked. Once the difference mean value has been obtained, the existing solution is updated in the teacher phase. The difference mean is added to the existing value to obtain the updated value. Of the two phases comprising the process of the algorithm, the teacher phase is the genesis of the algorithmic process. Students appreciate through contact with the teacher, who strives to improve student performance as reflected by the increase in the (mean) average result of the class. The main objective in TLBO is to approach the ideal value identified as the teacher. This resonates with the notion that the teacher is the best learner. The mean result is computed as the compounded product of the random value, variable mean, teaching factor (TF), and difference in best value. TF is randomly generated and is not a set parameter in the TLBO algorithm. From practice, the best results are obtained when TF is set as either 1 or 2 [38].
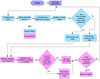 |
Fig. 3 TLBO flow chart. |
4.6.2 Learner phase
This is the final phase of the algorithm in which learners begin to interact through self-study. The main assumption for this stage is that there is no facilitation from the teacher and learners interact as peers. Through such interaction with greater fitness value learners, lower fitness value learners appreciate without any trade-off loss for the greater value learner. In this phase any two learners whose values are not similar are updated with respect to formulas premised on greatness of value. Furthermore, max/min structure of the objective is also a deciding factor. Depending on the population, this process will continue until the termination criterion is satisfied, failure to which the process returns to the learner phase. Summarily, in this manner the TLBO algorithm is executed.
5 Mathematical problem formulation
Two objectives, volume and center distance, have been considered for minimization on a spur gear train with three gears. The mathematical problem is reduced to a single-objective problem by applying the BOF method. By application of this method, the volume objective is then considered as the main objective, while center distance is treated as a constraint.
Subject to
5.1 AGMA and TLBO algorithm parameters
The TLBO algorithm is parameterless and is defined by the population and number of iterations. These parameters have been set as shown in Table 2.
On the other hand, the AGMA method is a gear design standard that defines gear design procedure. The methodology is defined by various formulas and design factors that are selected based on intended application of the design. The rim thickness factor is applied as 1 since the design ensures the minimum root thickness of gear is designed. The overload factor was chosen as 1.25 considering a uniform power from the tractor power takeoff and moderate shock from the tilling operations of the rotary tiller. The reliability factor was also chosen to represent failures less than 1 in 100. The size factor is taken as 1 due to proper selection of materials. Load distribution is taken as uniform and the operating temperature of gear blank to be less than 120 °C. Contact stress, surface condition, and elasticity factors are also applied as unitary due to normal conditions.
Therefore, the TLBO algorithm being a parameterless algorithm requires population and number of iterations that control are related to the convergence of the solution and search space. AGMA design factors relate to the various practical aspects of the design problem under study.
TLBO algorithm and AGMA method parameters.
6 Results and discussions
In this research work, a three-gear train system was optimized using the bounded objective method and TLBO algorithm. Two objectives, volume and center distance, were investigated with one main objective volume minimized while the other, center distance, treated as a constraint. The same gear train was also solved analytically using the AGMA design approach. A total of five variables, viz., face width, module, pinion, idler, and gear teeth, were investigated for the optimization problem. The results are shown in Table 3. Using AGMA design procedure, the center distance obtained was 253 mm, while 1.273 × 106 mm3 was realized as total volume of the gear system. The result obtained for center distance, using the TLBO algorithm, was 250 mm, which is approximately 3 mm less than that for AGMA method.
The volume was 1.005 × 106 mm3 reflecting 21% decrease in total volume. In terms of design variables, the AGMA result had higher values for module, hardness factor, pinion, and idler tooth numbers, while the face width value was lower than that obtained using TLBO.
AGMA and TLBO optimal results.
6.1 Variation study
Variation studies were performed for variables against objectives in order to determine their influence on objective functions. Center distance is a function of gear diameters that are defined by module and number of teeth. Studies on these two variables against center distance are represented in Figures 4 and 5 for two different gear ratios: 3.5 and 4.5. The linear relationship indicates a proportional increase in the objective induced by the variables under investigation. Though variation ranges for design variables differ in scale and range, there is a noticeable greater influence induced by module as compared to pinion teeth number.
Therefore, in order to achieve minimization of objectives for the rotary tiller, lower tooth number and module values need to be obtained. This is also reflected by the results obtained by applying TLBO as shown in Table 3, whereby module value is 3.94 compared to 5.294 obtained using the AGMA method analytically.
With regard to face width, there is no direct relationship to center distance. However, there exists a linear relationship between volume and face width, as shown in Figure 6. Module and volume exhibit a parabolic curve. The change in volume per standard module variation increases as the value of module appreciates, as shown in Figure 7 and similarly for pinion tooth number in Figure 8. In this study, it can be shown that the four-variables module, face width, and pinion tooth numbers that affect the physical properties of a gear system influence the two objectives differently. While considering these variables as dimensionless against the volume objective, Figure 9 shows that module has the greatest influence on volume, followed by face width and pinion tooth numbers. Another important variable considered in this research work is hardness, which is a factor that is related to material choice. The hardness value determines the bending and contact stress values that are compared with the allowable stress values to determine safety factors. In this research work, bending and contact stress are evaluated as constraints. Hardness factor and stress are compared for bending and contact stress evaluations in Figure 10. The two lines shown represent variations in bending and contact stress for the range under investigation. The results indicate that there is a higher risk to bending as compared to contact stress. For a hardness factor range of 150–400, there is 12.4% variation in bending stress as compared to 51% variation for contact stress. This means that material selection is more critical when considering bending stress. Practically, bending fatigue failure is proven to be the major cause of gear failure [39] and in a study carried out by Akinci et al. [20], bending fatigue accounted for at least 61% of failures. Furthermore, 74.7% of failures were due to usage faults that are mostly overloading of gear systems resulting in fracture.
 |
Fig. 4 Center distance and module variation. |
 |
Fig. 5 Center distance and pinion tooth number variation. |
 |
Fig. 6 Volume and face width variation. |
 |
Fig. 7 Volume and module variation. |
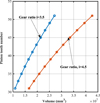 |
Fig. 8 Volume and pinion tooth variations. |
 |
Fig. 9 Volume, module, face width, and pinion tooth number. |
 |
Fig 10 Stress, hardness variation for bending, and contact stress. |
6.2 Validation
The AGMA and TLBO results obtained were validated against results in literature and those obtained by geometric modeling, as shown in Table 4. It was observed that there was a 44% improvement in volume between AGMA results and reference [20], while a 55% reduction was obtained using TLBO and the geometric model results. In terms of center distance, percentage change was 23% for both AGMA and geometric model results and 24% for TLBO results against reference [20]. Using a computer-aided software, the gear train systems were modeled and evaluated for optimal volume reflecting a variance of 0.01 against the TLBO result, while 0.257 and 1.27 values were obtained for AGMA and reference [20] comparisons with TLBO.
Validation of the study.
7 Conclusions
Multiobjective optimization of a three-gear train was conducted with volume and center distance as objectives. A total of five variables, viz., face width, module, number of pinion teeth, idler teeth number, and material hardness were considered. The gear model was formulated to explore the minimization of volume, center distance in order to reduce material, and its associated cost. In order to solve the problem as a single-objective formulation using TLBO, a BOF method was applied treating center distance as a constraint while minimizing volume. The example problem was adopted from Akinci et al. [20] focusing on a rotary tiller. Two methodologies AGMA and TLBO were applied to solve the design problem. The obtained results were validated through a geometric model generated using SolidWorks CAD software for the given optimal set of designing parameters. Variation studies were conducted to determine parameter influence on the gear train system.
The major outcomes of the research work are summarized as follows:
-
It is observed that there is a 55% improvement in the solution when TLBO is applied to solve the gear design problem, thereby reflecting the ability of the TLBO algorithm to improve optimal result.
-
It is observed that center distance and volume objectives are directly related and that increase/decrease in one result will induce increase/decrease in the other.
-
It is observed that the influence ranking for the geometric design variables is module, face width, pinion tooth number, respectively, for the minimum volume objective, while face width has no relation with center distance.
-
It is observed that geometric models can be used to validate optimal results as reflected by the small variance and utilization by other authors such as Wang et al. [40].
-
Optimization techniques can search the solution space efficiently and with less resources expended as compared to iterative procedures and the consideration of center distance and volume results in a distinct gearbox configuration that has a higher length-to-width ratio.
-
It is observed that there is a greater risk from bending than from contact stress for spur gears, while stress variation is higher for the latter at 51% than the former at 12.4%.
Nomenclature
B, F : face width, net face width (mm)
z1, zi, z2 : number of teeth on pinion, idler, gear
KB Ko Kv Ks Km : rim thickness, overload, dynamic, size, load distribution factor
KT KR CH : temperature, reliability, contact stress factor
J : geometry factor of bending stress
ZN, YN : stress cycle factor for contact stress, bending strength
Cf Cp : surface condition factor, elasticity coefficient
D1−4 : gear diameters for gears 1–4 (mm)
Tin, To : input, output torque (Nm)
Vol, Vpinion, Vidler,Vgear : total volume, volume of pinion, idler, gear (mm3)
σat : allowable bending stress (N/mm2)
σac : allowable contact stress (N/mm2)
Sh , Sf : safety factor for bending, contact stress
LINMAP: Linear programming for multidimensional analysis of preference
TOPSIS: Technique for order of preference by similarity to ideal solution
References
- A. Osyczka, An approach to multicriterion optimization problems for engineering design. Comput. Methods Appl. Mech. Eng. 15 , 309–333 (1978) [CrossRef] [Google Scholar]
- B.S. Tong, D. Walton, The optimisation of internal gears. Int. J. Mach. Tools Manuf. 27 , 491–504 (1987) [CrossRef] [Google Scholar]
- S. Prayoonrat, D. Walton, Practical approach to optimum gear train design. Comput. Des. 20 , 83–92 (1988) [Google Scholar]
- K. Deb, A. Pratap, S. Agarwal, T. Meyarivan, A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 6 , 182–197 (2002) [Google Scholar]
- R.V. Rao, Teaching learning based optimization algorithm. New York: Springer 2016 [CrossRef] [Google Scholar]
- T. Yokota, T. Taguchi, M. Gen, A solution method for optimal weight design problem of the gear using genetic algorithms. Comput. Ind. Eng. 35 , 523–526 (1998) [CrossRef] [Google Scholar]
- V. Savsani, R.V. Rao, D.P. Vakharia, Optimal weight design of a gear train using particle swarm optimization and simulated annealing algorithms. Mech. Mach. Theory 45 , 531–541 (2010) [CrossRef] [Google Scholar]
- S. Golabi, J.J. Fesharaki, M. Yazdipoor, Gear train optimization based on minimum volume/weight design. Mech. Mach. Theory 73 , 197–217 (2014) [CrossRef] [Google Scholar]
- D. Das, S. Bhattacharya, B. Sarkar, Decision-based design-driven material selection: a normative-prescriptive approach for simultaneous selection of material and geometric variables in gear design. J. Materials Design 92 , 787–793 (2016) [Google Scholar]
- N. Kostić, N. Marjanović, N. Petrović, A novel approach for solving gear train optimization. Int. J. Veh. Mech. Eng. Transp. Syst. 42 , 67–76 (2016) [Google Scholar]
- N. Marjanovic, B. Isailovic, V. Marjanovic, Z. Milojevic, M. Blagojevic, M. Bojic, A practical approach to the optimization of gear trains with spur gears, Mech. Mach. Theory. 53 , 1–16 (2012) [Google Scholar]
- A. Zolfaghari, M. Goharimanesh, A.A. Akbari, Optimum design of straight bevel gears pair using evolutionary algorithms, J. Brazilian Soc. Mech. Sci. Eng. 39 , 2121–2129 (2017) [Google Scholar]
- R. Sanghvi, A. Vashi, H.P. Patolia, R.G. Jivani, Multi-objective optimization of two-stage helical gear train using NSGA-II, J. Optim. 2014 , 670297 (2014) [Google Scholar]
- K. Tamboli, S. Patel, P.M. George, R. Sanghvi, Optimal design of a heavy duty helical gear pair using particle swarm optimization technique. Proc. Technol. 14 , 513–519 (2014) [CrossRef] [Google Scholar]
- D.F. Thompson, S. Gupta, A. Shukla, Tradeoff analysis in minimum volume design of multi-stage spur gear reduction units. Mech. Mach. Theory 35 , 609–627 (2000) [CrossRef] [Google Scholar]
- K. Deb, S. Jain, Multi-speed gearbox design using multi-objective evolutionary algorithms. J. Mech. Des. 125 , 609 (2003) [CrossRef] [Google Scholar]
- J. Stefanović-Marinović, S. Troha, M. Milovančević, An application of multicriteria optimization to the two-carrier two-speed planetary gear trains. Facta Univ. Ser. Mech. Eng. 15 , 85 (2017) [CrossRef] [Google Scholar]
- R. Arora, S.C. Kaushik, R. Kumar, R. Arora, Soft computing based multi-objective optimization of Brayton cycle power plant with isothermal heat addition using evolutionary algorithm and decision making. Appl. Soft Comput. J. 46 , 267–283 (2016) [CrossRef] [Google Scholar]
- R. Kumar, S.C. Kaushik, R. Kumar, R. Hans, Multi-objective thermodynamic optimization of an irreversible regenerative Brayton cycle using evolutionary algorithm and decision making. Ain Shams Eng. J. 7 , 741–753 (2016) [CrossRef] [Google Scholar]
- I. Akinci, D. Yilmaz, C. Murad, Failure of a rotary tiller spur gear. Eng. Falure Anal. 12 , 400–404 (2005) [CrossRef] [Google Scholar]
- A.L. Kapelevich, Direct gear design, 1st ed. New York: Taylor & Francis 2013 [CrossRef] [Google Scholar]
- G. Madhusudan, C.R. Vijayasimha, Approach to spur gear design. Comput. Des. 19 , 555–559 (1987) [Google Scholar]
- J. Arora, Introduction to optimum design, 3rd ed. Cambridge: Academic Press 2011 [Google Scholar]
- R.A. El-Sehiemy, A.A. Abou, E.L. Ela, A. Shaheen, A Multi-objective fuzzy-based procedure for reactive power-based preventive emergency strategy. Int. J. Eng. Res. Afr. 13 , 91–102 (2015) [CrossRef] [Google Scholar]
- A. Khan, K. Maity, Parametric optimization of some non-conventional machining processes using MOORA method. Int. J. Eng. Res. Afr. 20 , 19–40 (2016) [CrossRef] [Google Scholar]
- O.M. Koura, A.S. El-Akkad, Optimization of cutting conditions using regression and genetic algorithm in end milling. Int. J. Eng. Res. Afr. 20 , 12–18 (2016) [CrossRef] [Google Scholar]
- R. Arora, S.C. Kaushik, R. Arora, Thermodynamic modeling and multi-objective optimization of two stage thermoelectric generator in electrically series and parallel configuration. Appl. Therm. Eng. 103 , 1312–1323 (2016) [CrossRef] [Google Scholar]
- R. Arora, S.C. Kaushik, R. Kumar, R. Arora, Multi-objective thermo-economic optimization of solar parabolic dish Stirling heat engine with regenerative losses using NSGA-II and decision making. Int. J. Electr. Power Energy Syst. 74 , 25–35 (2016) [CrossRef] [Google Scholar]
- R. Arora, S.C. Kaushik, R. Kumar, Multi-objective thermodynamic optimization of solar parabolic dish Stirling heat engine with regenerative losses using NSGA-II and decision making. Appl. Sol. Energy 52 , 295–304 (2016) [Google Scholar]
- R. Arora, S.C. Kaushik, R. Kumar, Multi-objective thermodynamic optimisation of solar parabolic dish Stirling heat engine using NSGA-II and decision making. Int. J. Renew Energy Technol. 8 , 64–92 (2017) [Google Scholar]
- R. Arora, R. Arora, Multiobjective optimization and analytical comparison of single‐ and 2‐stage (series/parallel) thermoelectric heat pumps, Int. J. Energy Res. 42 , 1760–1778 (2018) [CrossRef] [Google Scholar]
- R. Arora, R. Arora, Multicriteria optimization based comprehensive comparative analyses of single-and two-stage (series/parallel) thermoelectric generators including the influence of Thomson effect. J. Renew Sustain. Energy 10 , 044701 (2018) [Google Scholar]
- R. Arora, S.C. Kaushik, R. Arora, Multi-objective and multi-parameter optimization of two-stage thermoelectric generator in electrically series and parallel configurations through NSGA-II. Energy 91 , 242–254 (2015) [CrossRef] [Google Scholar]
- R. Arora, S.C. Kaushik, R. Kumar, Multi-objective optimization of an irreversible regenerative Brayton cycle using genetic algorithm, in 2015 International Conference on Futuristic Trends on Computational Analysis and Knowledge Management (ABLAZE). IEEE, pp. 340–346 (2015) [Google Scholar]
- R. Arora, S.C. Kaushik, R. Kumar, Multi-objective optimization of solar powered Ericsson cycle using genetic algorithm and fuzzy decision making, in 2015 International Conference on Advances in Computer Engineering and Applications (ICACEA). IEEE, pp. 553–558 (2015) [Google Scholar]
- A. Messac, Optimization in practice with MATLAB: for engineering students and professionals. Cambridge : Cambridge University Press (2015) [CrossRef] [Google Scholar]
- S.S. Rao, Engineering optimization: theory and practice, 4th ed. New York: John Wiley & Sons, Inc 2009 [CrossRef] [Google Scholar]
- R. Venkata Rao, Review of applications of TLBO algorithm and a tutorial for beginners to solve the unconstrained and constrained optimization problems. Decis. Sci. Lett. 5, 1–30 (2016) [Google Scholar]
- Available at http://gearsolutions.com/departments/materialsmatter-common-gear-failures/ [Google Scholar]
- C. Wang, S. Wang, G. Wang, Volume models for different structures of spur gear. Aust. J. Mech. Eng. 1–9 (2017). DOI: 10.1080/14484846.2017.1381373 [Google Scholar]
Cite this article as: Edmund S. Maputi, Rajesh Arora, Design optimization of a three-stage transmission using advanced optimization techniques, Int. J. Simul. Multidisci. Des. Optim. 10, A8 (2019)
All Tables
All Figures
 |
Fig. 1 Rotary tiller gear train system. |
| In the text | |
 |
Fig. 2 AGMA design procedure for spur and helical gears. |
| In the text | |
 |
Fig. 3 TLBO flow chart. |
| In the text | |
 |
Fig. 4 Center distance and module variation. |
| In the text | |
 |
Fig. 5 Center distance and pinion tooth number variation. |
| In the text | |
 |
Fig. 6 Volume and face width variation. |
| In the text | |
 |
Fig. 7 Volume and module variation. |
| In the text | |
 |
Fig. 8 Volume and pinion tooth variations. |
| In the text | |
 |
Fig. 9 Volume, module, face width, and pinion tooth number. |
| In the text | |
 |
Fig 10 Stress, hardness variation for bending, and contact stress. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.