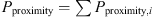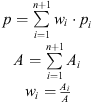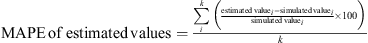| Issue |
Int. J. Simul. Multisci. Des. Optim.
Volume 7, 2016
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 11 | |
| DOI | https://doi.org/10.1051/smdo/2016009 | |
| Published online | 24 November 2016 | |
Research Article
Lightweight parametric optimisation method for cellular structures in additive manufactured parts
1
Departamento de Ingeniería Mecánica, Universidad de Las Palmas de Gran Canaria, 35017
Las Palmas G.C., Spain
2
University Institute of Computational Engineering (SIANI), Evolutionary Computation and Applications (CEANI), Universidad de Las Palmas de Gran Canaria, 35017
Las Palmas G.C., Spain
3
Brunel University London, College of Engineering, Design and Physical Sciences, Department of Design, Tower A, TOWA020, UB8 3PH, UK
* e-mail: ruben.paz@ulpgc.es
Received:
30
June
2016
Accepted:
27
October
2016
The application of cellular structures in additive manufactured parts combined with lightweight optimisation has an enormous potential, reducing weight, production time and cost. This paper presents a new method based on design of experiments, metamodels and genetic algorithms (combined with Computer Aided Design and Finite Element Method tools) to accomplish lightweight parametric optimisation of cellular structures in additive manufactured parts. Some specific strategies were implemented in the developed optimisation method to improve the performance compared with conventional methods. These strategies intensify the sampling for the surrogate model refinement in areas close to the feasible/unfeasible border, where the optimum is expected. The method was tested in different case studies and compared with a conventional optimisation tool based on the Box-Behnken design of experiments and the response surface method metamodel. The proposed method enhances the results (3–4.2% of improvement) in all the case studies, with a similar optimisation time. Compared with a previous version created during the development of the methodology, the final version achieves a similar quality of the optimum in lower optimisation time.
Key words: Design optimisation / Additive manufacturing / Genetic algorithm / Finite element analysis / Computer-aided design
© R. Paz et al., Published by EDP Sciences, 2016
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The progressive advancement of developing new materials and processes in Additive Manufacturing (AM) has led to a greater uptake of AM systems [1, 2]. AM allows highly complex parts with overhangs and undercuts that are costly or impossible to be produced using conventional manufacturing.
The definition of internal cellular structures within an additive manufactured part allows reducing the weight compared with the solid geometry. By optimising these internal structures, there is a potential to minimise material and weight, thus reducing the overall production cost and time. This concept has been applied in tissue engineering [3–6] and can potentially benefit other high-end industries such as aerospace or automotive sectors. This paper proposes an intelligent optimisation algorithm to optimise the design of the internal cellular structures (Figure 1). Computer Aided Design and Finite Element Method tools (CAD and FEM) are used to define and simulate the internal geometries, thus analysing its behaviour under different load conditions without accomplishing real tests.
 |
Figure 1. Proposed workflow for lightweight optimisation of AM parts. |
Some authors have proposed integrating lightweight modelling (with complex structures) by combining CAD software with other tools to optimise the geometry [7–12]. Those parametric modelling techniques approximate the part surface with Bezier surface patches, then enable the truss generation between the patches and finally combine different optimisation techniques to optimise the geometry [13, 14]. Although these proposals are interesting, a complex workflow is needed between different programs as well as manual work to decompose the external surfaces. Nevertheless, this paper aims to create a simple cellular structure by repeating a hollow pattern and optimise it by specific optimisation algorithms.
On the other hand, most of the commercial CAD-FEM software are able to achieve topology optimisation [15–17]. However, these optimisation techniques may lead to designs that cannot be manufactured by AM because of the manufacturing constraints, such as small wall thickness, problems with the removal of support material (if needed), and so on. In fact, this is a matter of discussion on recent research. Some authors have analysed the capabilities of different topology optimization techniques, concluding that the designs obtained by these methods usually require post-processing in order to be manufacturable [18]. Other authors have proposed filters to face problems related to overhang angles [19, 20], but many other problems should be taken into account to guarantee a printable design. This work focuses on parametric optimisation, which allows controlling the constraints associated with the manufacturing process by the proper definition of the limits of the design variables. Therefore, the capabilities of the AM machine must be known to correctly define the limits of the design variables before the simulation is run.
Regarding the optimisation strategy, Genetic Algorithms (GAs) and FEM simulations [21] are widely used to accomplish the optimisation process. However, they are usually combined with surrogate models to reduce the number of FEM simulations and, consequently, the optimisation time [22, 23]. There are several parametric optimisation tools available in commercial CAD-FEM software, mainly based on Design of Experiments (DOE) and surrogate models (also known as metamodels). DOE consists in simulating some specific designs (among the infinite possible designs of the search domain). The data obtained are used to create the surrogate model, which predicts the results of any design proposed during the optimisation without accomplishing the FEM simulations.
Different commercial CAD-FEM softwares have this type of optimisation tools. Catia (Dassault Systèmes, Vélizy-Villacoublay, France) includes conjugate gradients or simulated annealing [24]. Conjugate gradients needs the first derivative of the objective function (usually unknown), while simulated annealing is a stochastic method that requires a too high number of simulations. In the case of SolidWorks (Dassault Systèmes, Vélizy-Villacoublay, France), there is an optimisation tool based on Box-Behnken DOE [25, 26] and the response surface method (RSM, regression model). However, this optimisation tool has not refinement strategies for the RSM. As a consequence, the predicted optimum may comply with the optimisation constraints according to the estimates of the RSM surrogate model, but when simulated by FEM, maybe the design does not comply with the constraints. Consequently, in some cases, the tool finishes the process without giving a solution to the optimisation problem. ANSYS (ANSYS, Inc., Canonsburg, Pennsylvania, USA) also includes many powerful tools for optimisation. It has different DOE strategies such as central composite design (CCD) or Box-Behnken design. Box-Behnken DOE requires fewer levels (and hence lower sampling effort) than CCD [27]. Regarding metamodels, ANSYS also has different options such as RSM, Kriging [28], or Neural Networks (NN). As mentioned before, RSM is a regression model that fits one or two-order polynomials to the data. On the other hand, Kriging is an interpolation method (exact prediction on the data) that takes into account the space data distribution to create the metamodel. Finally, NN is a learning method inspired by the operation of the nervous system. In general terms, RSM is recommended for optimisation problems with small number of design variables, while Kriging and NN are recommended for large number of design variables (NN typically for complex problems with a larger number of sampling points) [29]. However, only Kriging includes refinement strategies. This refinement consists in adding new sampling points in the zones with the higher fitting error. This enables improving the accuracy of the metamodel, but also means more computational time.
Although this latter tool is very interesting, the improvement of the metamodel is applied in the zones with the highest fitting error. However, this refinement can be potentially applied in the feasible/unfeasible border where the optimum will be located. By doing this, the surrogate model would have a better performance, reducing the optimisation time. This is the main contribution of the proposed method.
2 New approach: increase of the sampling density in the feasible/unfeasible border
The method proposed in this work (Figure 2) consists in applying an initial DOE to create a surrogate model and then refine it through the simulation of new designs located in regions of interest. The main idea is to apply the refinement in specific areas to improve the performance of the surrogate model. Once the surrogate model has achieved a certain level of accuracy, the optimal design is searched by using GAs and the predictions of the metamodel.
 |
Figure 2. Flow chart of the general approach. |
The design variables are associated with the dimensions of the cellular geometries inside the part. These variables have a monotonic relationship with the overall structure, which means that an increase of a variable associated with the size of the hollow cells results in a mass reduction. Moreover, the most commonly analysed mechanical properties in the design process (stiffness and strength) are also reduced. Therefore, for these optimisation cases, the constraints usually have an opposite behaviour compared to the mass. As a result, the optimum design will be located in the feasible/unfeasible border (Figure 3).
 |
Figure 3. Feasible/unfeasible border in a 2-D problem. |
To take advantage of this statement, the approach presented consists in placing the new sampling points (needed for the DOE and the metamodel refinement) close to the feasible/unfeasible border, thus raising the density of sampling in the zone where the optimum will be found. This strategy intensifies the refinement of the surrogate model in the feasible/unfeasible border, which means that the accuracy of the predictions is improved in the zones where the optimisation algorithm will find the optimum. As a result, the performance of the optimisation method will be enhanced (better quality of the optimum with a similar CPU time).
3 Optimisation case studies
This section presents some of the case studies used to test the optimisation strategies developed in this work. The three first case studies explained below were based on a mini wind blade (Figure 4 and Sects. 3.1–3.3), and the fourth is based on the stem of a bicycle (see Sect. 3.4). The goal, in the case of the blade, is to minimise its weight by optimising the values of the design variable associated with the internal cellular structure. The maximum deflection must be lower than 15 mm (constraint) when a 50N load is applied. This type of constraint (minimum stiffness under a specific static load) is quite common in the mechanical tests of blades and other mechanical components. The material is ABSP400 for Fused Deposition Modelling (FDM).
 |
Figure 4. Geometry of the blade case study. |
This blade was lightened using different type of cellular structures to test the optimisation method with different number of design variables. Three different internal designs are presented below, with 3, 4 and 5 design variables respectively.
The boundary conditions were the 50 N vertical load uniformly distributed on the lower face and the constrained movement in all the directions on the surface of the joint between the blade and rotor (root of the blade). The curvature-based mesher was selected since it has more flexibility to mesh different geometries and refines the mesh according to the curvature of the geometry. Parabolic tetrahedral elements were used. The minimum and maximum element size was 0.25 mm and 35 mm respectively. The total number of nodes was around 120,000, ensuring a good aspect ratio of the elements and quality of the mesh.
3.1 Blade with 3 design variables
Three different design variables were used to define an internal cubic hollow structure. Figure 5 shows a section of the blade near the root (the thickest zone) to depict the three design variables of the internal cubic hollows. The variables were the length of the sides of the cubic hollow (“L”, limits between 20–60 mm), the external thickness (“e”, limits between 3–8 mm) and the thickness between the cubic hollows (“e_h”, limits between 3–8 mm).
 |
Figure 5. Design variables for a cubic hollow structure (blade section, 3 variables). |
The optimisation problem can be summarised as:
Minimise mass (L, e, e_h)
Subject to max_deflection ≤ 15 (mm)
20 ≤ L ≤ 60 (mm)
3 ≤ e ≤ 8 (mm)
3 ≤ e_h ≤ 8 (mm)
Individual (L, e, e_h)
3.2 Blade with 4 design variables
In the case of 4 design variables, the hollows had the shape of square prisms (Figure 6). The variables were the side of the squared base (“L”, 20–60 mm), the external thickness (“e”, 3–8 mm), the thickness between the hollows (“e_h”, 3–8 mm) and the height of the hollows (“h”, 20–60 mm).
 |
Figure 6. Design variables for a square prism (blade section, 4 variables). |
The optimisation problem can be summarised as:
Minimise mass (L, e, e_h, h)
Subject to max_deflection ≤ 15 (mm)
20 ≤ L ≤ 60 (mm)
3 ≤ e ≤ 8 (mm)
3 ≤ e_h ≤ 8 (mm)
20 ≤ h ≤ 60 (mm)
Individual (L, e, e_h, h)
3.3 Blade with 5 design variables
In the case of 5 design variables (Figure 7), the hollows were rectangular prisms, defined by both sides of the rectangle (“L1”, 20–60 mm) and (“L2”, 20–60 mm), the external thickness (“e”, 3–8 mm), the thickness between the hollows (“e_h”, 3–8 mm) and the height of the hollows (“h”, 20–60 mm).
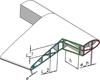 |
Figure 7. Design variables for a rectangular prism (blade section, 5 variables). |
The optimisation problem can be summarised as:
Minimise mass (L1, L2, e, e_h, h)
Subject to max_deflection ≤ 15 (mm)
20 ≤ L1 ≤ 60 (mm)
20 ≤ L2 ≤ 60 (mm)
3 ≤ e ≤ 8 (mm)
3 ≤ e_h ≤ 8 (mm)
20 ≤ h ≤ 60 (mm)
Individual (L1, L2, e, e_h, h)
3.4 Stem (5 design variables)
The stem of a bicycle was also used to test the final version of the optimisation. The goal is to minimise the weight of the stem using a prismatic hollow structure similar to the one applied in the blade with 5 variables. The maximum deflection must be lower than 6 mm when a load of 1000N is applied. Figure 8 shows the design variables used in this case. The limits of the design variables were “Lx” (5–50 mm), “Ly” (10–40 mm), “Lz” (20–150 mm), “e” (1–20 mm) and “e h ” (1–20 mm). ABSP400 was also used.
 |
Figure 8. Design variables for the stem of a bicycle. |
The boundary conditions were the 1000N vertical load uniformly distributed on the internal cylindrical face of the stem (horizontal axis) and the constrained movement in all the directions on the internal cylindrical face (vertical axis). The curvature-based mesher was selected. Parabolic tetrahedral elements were used, with a minimum and maximum element size of 0.5 mm and 10 mm respectively. These values were selected since they guaranteed a good aspect ratio of the elements and no problems were found with the different designs meshed.
The optimisation problem can be summarised as:
Minimise mass (Lx, Ly, Lz, e, eh)
Subject to max_deflection ≤ 6 (mm)
5 ≤ Lx ≤ 50 (mm)
10 ≤ Ly ≤ 40 (mm)
20 ≤ Lz ≤ 150 (mm)
1 ≤ e ≤ 20 (mm)
1 ≤ eh ≤ 20 (mm)
Individual (Lx, Ly, Lz, e, eh)
4 New parametric optimisation method based on DOE, feasible/unfeasible border approximation, addition of new middle points, border approximation by GAs and final GA
This section presents the functioning of the final optimisation algorithm developed in this research. SolidWorks software was used as a CAD-FEM tool. The optimisation method was implemented in a subroutine of Matlab (The MathWorks, Inc, Natick, Massachusetts, USA). The previous case studies were used to test the different optimisation versions developed until the final one was achieved. Therefore, the final methodology was the result of the evolution of different versions that were improved progressively through the analysis of the results obtained in different case studies. The final methodology was compared not only with the previous versions, but also with a standard optimisation tool available in SolidWorks, which is based on Box-Behnken DOE and estimation of the optimum by the RSM metamodel (BBRS method). The aim of the comparison is to validate if the new method improves the quality of the optimum (lower weight) without increasing the optimisation time. Since the main CPU time of the optimisation process is associated with the number of FEM simulations, the optimisation time was compared through the total number of designs simulated.
The new method was developed to specifically intensify the sampling in the feasible/unfeasible border. Several steps are carried out to address the optimisation process. Figure 9 summarises the overall optimisation process.
 |
Figure 9. Flow chart of the optimisation method (version 3). |
Step 1: DOE (2n + central point)
The first stage is a 2-level full factorial DOE with central point. Each point or design is simulated by FEM to evaluate the mechanical behaviour and then save the data of interest (constraints and weight).
Step 2: Feasible/unfeasible border approximation
A phase of border approximation along the edges is carried out. This stage automatically identifies the edges cut by the feasible/unfeasible border in accordance to the results obtained in the corners with the 2-level full factorial DOE. Based on the results of the two vertices of the edge, a new point is added between the vertices, using Hermite interpolation [30] to determine the location of the new point (to reach the feasible/unfeasible border). In previous versions of the algorithm, linear interpolation was used, but the convergence was slower. Hermite polynomial interpolation showed better results even than splines (no oscillations, Figure 10). This stage is repeated in a loop until the deviation of the more restrictive constraint is less than 5% of the limit value. This idea was initially applied in all the edges cut by the feasible/unfeasible border. However, after several tests with different geometries and taking into account the next steps of the algorithm, it was observed a pattern of behaviour that could be used to reduce the number of sampling points needed for this stage. After this observation, the border approximation along the edges was programmed so that the approximation was carried out only along certain edges. The algorithm identifies the best corner of the cut across edges and then does the approximation along the cut across edges containing this corner.
 |
Figure 10. Comparison of different interpolation methods. |
Step 3: Addition of new middle points
In the next step, the programme identifies the best design added in the last iteration of the previous phase. Geometrically, this point represents the best corner (lower weight) of the feasible/unfeasible border. Then, new middle points are added between this point and the remaining adjacent corners of the feasible/unfeasible border (the last points added in the border approximation stage).
Figure 11 shows the concept of these three first steps in a 3D problem. The cube represents the search domain and the curved lines the unknown feasible/unfeasible border. In Figure 11A, the black circles are the corners and the central point of the initial DOE (Step 1). In Figure 11B, the grey edges represent the edges that are cut across the feasible/unfeasible border. Among the corners of these edges, the best one is selected (grey point, Figure 11B) and the feasible/unfeasible border approximation is carried out along the grey edges that start from this point (Figure 11B (Step 2). The last point added on each edge will be a corner of the feasible/unfeasible border, as shown by the black triangles in Figure 11C. Among these, the best is selected (grey triangle in Figure 11D) and combined with the rest to add new middle points (grey circles in Figure 11D) (Step 3). The number of new middle points can vary depending on the shape of the feasible/unfeasible border.
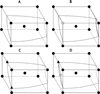 |
Figure 11. Steps of the new strategy for the border approximation phase. |
This proposal achieves a high sampling density close to the feasible/unfeasible border just with the information of the 2-level factorial DOE. According to different tests carried out, this strategy can achieve similar results to existing parametric optimisation methods with a reduced sampling, which means a lower optimisation time. The feasible/unfeasible border approximation along the edges (black triangles in Figure 11C) has demonstrated an improved performance in the optimisation. In most of the optimisation problems, there is a set of variables with a greater influence on the results. This leads to an optimum with most of the variables with their maximum or minimum value, which means optimums close to the corners of the feasible/unfeasible border (black triangles in Figure 11C).
Step 4: Border approximation by GAs
The next step consists in a border approximation by GAs. RSM based on a least square fitting of 2-order polynomials (LSF2) (1) is used to evaluate the fitness function during the GA evolution. This function is used to evaluate the quality of the designs proposed by the GA (mass plus penalties if they exist).
ue = estimated value by the least square fitting of 2-order polynomials (LSF2),
c0, ci, cij = fitting coefficients,
vari, varj = values of the design variables.
The best result achieved by the GA is analysed by the FEM and added to the database to upload the metamodel. This GA is executed again but penalising the individual points close to those points previously added in this phase of the program. This penalty, hereinafter called as “proximity penalty”, adds a value to the fitness function (2) if the point is too close to another added before (3), reducing its quality from the point of view of the GA. This strategy allows converging to a different optimum at each GA execution, which forces the system to explore new zones (similar concept to the resource sharing method used in multimodal optimisation [31, 32]) along the feasible-unfeasible border. This step is repeated until “n” points have been added. After that, the GA is run again but without applying the proximity penalty.
F = fitness function,
Pconstraints = penalization due to violation of the constraints.
Pproximity, i = 0, if the distance (di) between the individual and the sampling point “i” is higher than the radius of influence established,
Pproximity, i = 1/di × 1099, if the distance between the individual evaluated and the sampling point “i” is lower than the radius established.
The GA is repeated again, but in this case the metamodel employed is linear interpolation based on Delaunay triangulation (LIDT) (4). In previous versions, this metamodel was utilised in all the optimisation process. However, through different tests it was observed that the use LSF2 in the first stages of the optimisation process improved the initial convergence to the optimum design. Nevertheless, since LSF2 is a regression model, when the sampling is intensified in a specific zone the metamodel suffers from distortion and the optimisation algorithm does not converge to the optimum. Therefore, an interpolation metamodel is more suitable for the final steps of the optimisation algorithm. For this reason, once added “n + 1” points in this stage, the metamodel used is LIDT. In conclusion, LSF2 metamodel (regression method) can be useful in the early stages, where a general idea of the system behaviour is needed, while LIDT (interpolation method) is more appropriated for the final GA, where more accurate results are needed.
p = estimated value of a point inside a Delaunay element (triangles in 2D). The value is obtained as linear combination of the known values of the triangle vertexes,
pi = data value of vertex “i”,
wi = weight of vertex “i”,
n = number of design variables (in 2D, 2 variables),
A = area of the Delaunay element (triangle in 2D),
Ai = area of the sub-element “i”. In a 2D problem, the triangle shaped between the point to be estimated and the vertexes opposite to vertex “i”.
Once the GA evolves to the optimum using the estimates of the LIDT metamodel, that design is simulated by FEM and the algorithm evaluates the mean absolute percentage error (MAPE) (5) of the estimations in comparison with the simulation results, taking into account all the results of the constraints and the objective (weight of the part). If the MAPE is higher than 5%, the metamodel is uploaded with the results of this point and this GA is run again. Otherwise, the optimisation continues to the next stage. This loop guarantees a certain level of accuracy of the metamodel in the zones close to the final optimum.
k = number of sampling points,
i = sampling point evaluated.
Step 5: Final GA
To end the optimisation, a final GA is run (using the LIDT estimations to calculate the fitness function of each individual of the GA). The best individual is simulated using FEM. If this design improves the results of the best design simulated so far, it will be the optimum. Otherwise, the outcome is added to the database and the LIDT is uploaded to execute again the GA. This stage is repeated until reaching a design that improves the best one obtained in the previous steps of the algorithm.
5 Results and discussion
In the case of the blade with 3 design variables, the optimum obtained (Figure 12) had a mass of 1635 g with 17 simulations, while the BBRS method achieved an optimum of 1690 g with 14 points. Therefore, the new method improved the optimum 3.3% with only 3 more sampling points. On the other hand, a previous version of the optimisation programme achieved an optimum of 1632 g with 22 sampling points, which means that the final version implemented in this work needed 2 less sampling points to achieve almost the same result, then reducing the optimisation time.
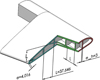 |
Figure 12. Section view of the optimum blade (3 design variables). |
In the case of 4 design variables, the optimum obtained with the final version had a mass of 1628 g after 27 FEM simulations (Figure 13). However, the BBRS method achieved an optimum of 1679 g with 26 points. Therefore, the result was improved 3.09% with only one more sampling point. On the other hand, the previous version of the optimisation programme obtained an optimum of 1639 g with 28 sampling points. Thus, the final methodology compared with the previous one, not only reduced the weight of the optimum, but also reduced the optimisation time.
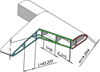 |
Figure 13. Section view of the optimum blade (4 design variables). |
In the case of 5 design variables, the final methodology achieved an optimum of 1590 g with 42 sampling points (Figure 14), while the BBRS method obtained an optimum of 1660 g with 42 sampling points. As a result, the proposed methodology improved the optimum 4.35% with the same optimisation time. On the other hand, the previous version achieved an optimum of 1601 g with 43 sampling points. Once again, the final version improved the quality of the optimum and reduced the optimisation time.
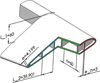 |
Figure 14. Section view of the optimum blade (5 design variables). |
In the case of the stem, the final methodology obtained and optimum of 1610 g with 48 sampling points, while the BBRS method achieved an optimum of 1679 g using 42 sampling points. The methodology presented improved the optimum 4.1% compared with the BBRS method, but required 6 more sampling points. Figure 15 shows the displacements of the optimal design.
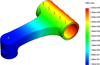 |
Figure 15. Displacements of the optimum design. |
Table 1 summarises the results obtained in the different case studies for the BBRS method, the previous version and the final version proposed in this paper. The last column shows the percentage quality improvement of the optimum obtained by the final version compared with the BBRS method (weight reduction). The methodology presented improves the results between 3 and 4.2% compared with the BBRS method with a similar sampling effort.
Results obtained in the case studies with the BBRS method, a previous version and the final methodology proposed.
On the other hand, the final version, compared with the previous one, reduces the sampling effort keeping a similar quality of the optimum.
An improved method to optimise cellular structures in additive manufacturing was presented based on a 2-level full factorial design of experiments and central point, border approximation along the edges, addition of new middle points between the best border corner and the adjacent corners, subsequent addition of new points along the feasible/unfeasible border using genetic algorithms with proximity penalty and least square fitting of 2-order polynomials and linear interpolation metamodels and, finally, a search of the optimum using a genetic algorithms combined with a linear interpolation metamodel. This proposal improves the results obtained by the optimisation method based on Box-Behnken design of experiments and optimum estimation by response surfaces (BBRS). Not only improves this new method the results with a similar sampling effort, but also ensures the achievement of the optimum thanks to the refinement loops included.
The border approximation phase along the edges results in an optimal design outcome with a low sampling. In many cases, the optimum is on the boundary of the domain because a variable can have a greater influence on the results than others. The proximity penalty in the genetic algorithm allows the addition of new points along the feasible/unfeasible border, thus exploring interesting zones. This phase is important when the surrogate model leads to an optimum output that is far away from the real optimum because of the prediction error made by the surrogate model. In these cases, the points added during this stage of the program can improve the fit of the surrogate model and, at the same time, explore new zones of the feasible/unfeasible border. The points added during this stage of exploration contribute by improving the fit of the metamodel in the area of interest near the optimum. Linear interpolation based on Delaunay triangulation and least square fitting (2-order polynomials) metamodels drastically reduced the number of numerical simulations. Least square fitting was found to be more effective in the early stages of the algorithm to obtain a general idea of the system behaviour, while linear interpolation was more appropriate for the final phase where more accurate estimates are needed.
The proposed methodology has enabled lightweight optimisation of cellular structures to be achieved for additive manufactured parts. The time has been reduced for the 3D CAD modelling of the cellular structure and the optimisation process itself. In terms of CAD modelling, this methodology enables a simple and fast generation of the 3D CAD structure within the same tool, which is a clear advantage compared with the references presented in Section 1, where manual work is needed as well as the interaction and workflow between different programs. Compared with the previous version developed, the final methodology reduces the optimisation time and achieves a similar quality of the optimum. On the other hand, the final version compared with the BBRS method improves the result 3.3% in a problem with 3 design variables, 3% in a problem with 4 design variables and 4.1 and 4.2% in two different problems with 5 design variables, keeping a similar optimisation time. These results should be highlighted because the BBRS method (Box-Behnken DOE and response surface) is the most efficient and fastest parametric optimisation strategy when dealing with a low number of design variables.
However, the method proposed shows a good performance only for problems with a low number of design variables (lower than 7). When the number of variables is higher, the sampling effort and the LIDT metamodel become a bottleneck for the optimisation process. For this reason, future research will investigate even more streamlined strategies when dealing with a larger number of design variables. These strategies will be also implemented using the Application Programming Interface available within the CAD/FEM software to automate the entire optimisation process. Once automated, this method will be able to be used by CAD designers, mechanical engineers or any AM user who wants to apply parametric lightweight optimisation in AM designs, allowing the application of this improved optimisation strategies for actual components.
Although this methodology can be applied with any Additive Manufacturing technology, the hollow structure of these case studies is oriented for FDM (Fused Deposition Modelling). The internal structure proposed consists of the repetition of a hollow pattern, which leads to internal hollows not connected between them. Since FDM can produce internal hollows, this technology would be the most appropriate. For other technologies such as SLS (Selective Laser Sintering), the type of pattern must be designed so that the powder trapped inside can be removed.
6 Conclusion
The proposed method allows the parametric lightweight optimization of internal cellular structures for AM parts. The algorithm uses specific strategies to improve the location of the sampling points, hence reducing the number of FEM simulations and time required. Moreover, the design and parameterization of the internal structure can be easily tackled and controlled through the correct definition of the limits of the design variables, ensuring the manufacturability of the designs obtained.
References
- Wohlers TT. 2014. Wohlers report 2014: 3D printing and additive manufacturing state of the industry annual worldwide progress report. Wohlers Associates: USA. [Google Scholar]
- Wong KV, Hernandez A. 2012. A review of additive manufacturing. ISRN Mechanical Engineering, 2012, e208760. DOI: 10.5402/2012/208760. [Google Scholar]
- Sachlos E, Czernuszka JT. 2003. Making tissue engineering scaffolds work. Review: the application of solid freeform fabrication technology to the production of tissue engineering scaffolds. European Cells & Materials, 5, 39–40. [Google Scholar]
- Yeong W-Y, Chua C-K, Leong K-F, Chandrasekaran M. 2004. Rapid prototyping in tissue engineering: challenges and potential. Trends in Biotechnology, 22, 643–652. DOI: 10.1016/j.tibtech.2004.10.004. [CrossRef] [Google Scholar]
- Yoo D-J. 2011. Computer-aided porous scaffold design for tissue engineering using triply periodic minimal surfaces. International Journal of Precision Engineering and Manufacturing, 12, 61–71. DOI: 10.1007/s12541-011-0008-9. [CrossRef] [Google Scholar]
- da Silva Bartolo PJ, Jorge MA, da Conceicao Batista F, Almeida HA, Matias JM, Vasco JC, Gaspar JB, Correia MA, Andre NC, Alves NF, Novo PP, Martinho PG, Carvalho RA. 2007. Virtual and rapid manufacturing: advanced research in virtual and rapid prototyping. CRC Press: USA. [Google Scholar]
- Chu C, Graf G, Rosen DW. 2008. Design for additive manufacturing of cellular structures. Computer-Aided Design and Applications, 5, 686–696. DOI: 10.3722/cadaps.2008.686-696. [CrossRef] [Google Scholar]
- Chang PS, Rosen DW. 2013. The size matching and scaling method: a synthesis method for the design of mesoscale cellular structures. International Journal of Computer Integrated Manufacturing, 26, 907–927. DOI: 10.1080/0951192X.2011.650880. [CrossRef] [Google Scholar]
- Rosen DW. 2007. Computer-aided design for additive manufacturing of cellular structures. Computer-Aided Design and Applications, 4, 585–594. [CrossRef] [Google Scholar]
- Wang H, Rosen DW. 2002. Parametric modeling method for truss structures, in ASME 2002 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, American Society of Mechanical Engineers, January, p.759–767. DOI: 101115/DETC2002/CIE-34495. [Google Scholar]
- Wang HV, Rosen DW. 2001. Computer-aided design methods for the additive fabrication of truss structure. School of Mechanical Engineering, Georgia Institute of Technology. [Google Scholar]
- Wang H, Chen Y, Rosen DW. 2005. A hybrid geometric modeling method for large scale conformal cellular structures, in ASME 2002 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, American Society of Mechanical Engineers, January, p.421–427. DOI: 10.1115/DETC2005-85366. [Google Scholar]
- Chu J, Engelbrecht S, Graf G, Rosen DW. 2010. A comparison of synthesis methods for cellular structures with application to additive manufacturing. Rapid Prototyping Journal, 16, 275–283. DOI: 10.1108/13552541011049298. [CrossRef] [Google Scholar]
- Rosen DW. 2007. Design for additive manufacturing: a method to explore unexplored regions of the design space, in Eighteenth Annual Solid Freeform Fabrication Symposium, Austin, Texas, USA. p. 402–415. [Google Scholar]
- Aremu A, Ashcroft I, Wildman R, Hague R, Tuck C, Brackett D. 2013. The effects of bidirectional evolutionary structural optimization parameters on an industrial designed component for additive manufacture. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 227, 794–807. DOI: 10.1177/0954405412463857. [CrossRef] [Google Scholar]
- Akin JE, Arjona-Baez J. 2001. Enhancing structural topology optimization. Engineering Computations, 18, 663–675. DOI: 10.1108/02644400110387640. [CrossRef] [Google Scholar]
- Lynch ME, Gu W, El-Wardany T, Hsu A, Viens D, Nardi A, Klecka M. 2013. Design and topology/shape structural optimisation for additively manufactured cold sprayed components. Virtual and Physical Prototyping, 8, 213–231. DOI: 10.1080/17452759.2013.837629. [CrossRef] [Google Scholar]
- Zegard T, Paulino GH. 2015. Bridging topology optimization and additive manufacturing. Structural and Multidisciplinary Optimization, 53, 175–192. DOI: 10.1007/s00158-015-1274-4. [CrossRef] [Google Scholar]
- Langelaar M. 2016. Topology optimization of 3D self-supporting structures for additive manufacturing. Additive Manufacturing, 12(Part A), 60–70. DOI: 10.1016/j.addma.2016.06.010. [CrossRef] [Google Scholar]
- Langelaar M. 2016. An additive manufacturing filter for topology optimization of print-ready designs. Structural and Multidisciplinary Optimization, 54(1), 1–13. DOI: 10.1007/s00158-016-1522-2. [CrossRef] [Google Scholar]
- Gätz R, Uebersax M, König O. 2000. Structural optimization tool using genetic algorithms and ansys,in Proc. 18. CAD-FEM User’s Meeting, Internationale FEM-Technologietage, Graf-Zeppelin-Haus, Friedrichshafen, June. [Google Scholar]
- Lee J-H, Hwang S-C, Park JH, Lee K-H. 2010. Structural design examples using metamodel-based approximation model, in Proceedings of the 9th WSEAS international conference on Applied computer and applied computational science World Scientific and Engineering Academy and Society (WSEAS), Stevens Point, Wisconsin, USA. p. 153–156. [Google Scholar]
- Pant S, Limbert G, Curzen NP, Bressloff NW. 2011. Multiobjective design optimisation of coronary stents. Biomaterials, 32, 7755–7773. DOI: 10.1016/j.biomaterials.2011.07.059. [CrossRef] [Google Scholar]
- König O, Wintermantel M. 2004. CAD-based evolutionary design optimization with CATIA V5, in Proceedings of 1st Weimar Optimization and Stochastic Days WOST, Weimar. p. 1–30. [Google Scholar]
- Eriksson L. 2008. Design of experiments: principles and applications. MKS Umetrics AB: Sweden. [Google Scholar]
- Kleijnen JPC. 2008. Design of experiments: overview. Social Science Research Network: Rochester, NY. [Google Scholar]
- Chen VCP, Tsui K-L, Barton RR, Meckesheimer M. 2006. A review on design, modeling and applications of computer experiments. IIE Transactions, 38, 273–291. DOI: 10.1080/07408170500232495. [CrossRef] [Google Scholar]
- Dressler M. 2009. Art of Surface Interpolation. Technical University of Liberec Faculty of Mechatronics and Interdisciplinary Engineering Studies: Czech Republic. [Google Scholar]
- Sakata S, Ashidaa F, Zakob M. 2004. An efficient algorithm for Kriging approximation and optimization with large-scale sampling data. Computer Methods in Applied Mechanics and Engineering, 193, 385–404. DOI: 10.1016/j.cma.2003.10.006. [CrossRef] [Google Scholar]
- Fritsch FN, Carlson RE. 1980. Monotone piecewise cubic interpolation. SIAM Journal on Numerical Analysis, 17, 238–246. [Google Scholar]
- Glibovets NN, Gulayeva NM. 2013. A review of niching genetic algorithms for multimodal function optimization. Cybernetics and Systems Analysis, 49, 815–820. DOI: 10.1007/s10559-013-9570-8. [CrossRef] [MathSciNet] [Google Scholar]
- Della Cioppa A, De Stefano C, Marcelli A. 2004. On the role of population size and niche radius in fitness sharing. IEEE Transactions on Evolutionary Computation, 8, 580–592. DOI: 10.1109/TEVC.2004.837341. [CrossRef] [Google Scholar]
Cite this article as: Paz R, Monzón MD, González B, Pei E, Winter G & Ortega F: Lightweight parametric optimisation method for cellular structures in additive manufactured parts. Int. J. Simul. Multisci. Des. Optim., 2016, 7, A6.
All Tables
Results obtained in the case studies with the BBRS method, a previous version and the final methodology proposed.
All Figures
 |
Figure 1. Proposed workflow for lightweight optimisation of AM parts. |
| In the text | |
 |
Figure 2. Flow chart of the general approach. |
| In the text | |
 |
Figure 3. Feasible/unfeasible border in a 2-D problem. |
| In the text | |
 |
Figure 4. Geometry of the blade case study. |
| In the text | |
 |
Figure 5. Design variables for a cubic hollow structure (blade section, 3 variables). |
| In the text | |
 |
Figure 6. Design variables for a square prism (blade section, 4 variables). |
| In the text | |
 |
Figure 7. Design variables for a rectangular prism (blade section, 5 variables). |
| In the text | |
 |
Figure 8. Design variables for the stem of a bicycle. |
| In the text | |
 |
Figure 9. Flow chart of the optimisation method (version 3). |
| In the text | |
 |
Figure 10. Comparison of different interpolation methods. |
| In the text | |
 |
Figure 11. Steps of the new strategy for the border approximation phase. |
| In the text | |
 |
Figure 12. Section view of the optimum blade (3 design variables). |
| In the text | |
 |
Figure 13. Section view of the optimum blade (4 design variables). |
| In the text | |
 |
Figure 14. Section view of the optimum blade (5 design variables). |
| In the text | |
 |
Figure 15. Displacements of the optimum design. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.