| Issue |
Int. J. Simul. Multisci. Des. Optim.
Volume 5, 2014
|
|
|---|---|---|
| Article Number | A08 | |
| Number of page(s) | 5 | |
| DOI | https://doi.org/10.1051/smdo/2013016 | |
| Published online | 06 February 2014 | |
Article
A multi-point constraints based layout design of multi-component systems
Engineering Simulation and Aerospace Computing, Northwestern Polytechnical University, 710072
Xi’an, Shaanxi, P.R. China
* e-mail: jh.zhu@nwpu.edu.cn
Received:
9
May
2013
Accepted:
23
October
2013
The primary purpose of this paper was to present an efficient method to implement the layout design of multi-component systems. In this study, two kinds of design variables: topology variables and geometry variables are simultaneously optimized to maximize the structure stiffness. The multi-point constraints (MPC) are used to simulate the connection behavior between these movable components and supporting structure. So during the optimization iterations, mesh regeneration caused by moving components is avoided compared to the linkage of nodal coincidence. At the same time, the precise geometry shapes and properties of components are maintained to reduce the model building error. At the last of the paper, the numerical example is presented to show the validity of this method.
Key words: Multi-component systems / Multi-point constraints / Layout optimization / Topology optimization
© H.-H. Gao et al., Published by EDP Sciences, 2014
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Topology optimization for continuum structures came out since the original idea of homogenization-based design method was proposed in the work of Bendsøe and Kikuchi [1]. More efforts including Solid Isotropic Material with Penalization (SIMP), Rational Approximation of Material Properties (RAMP) and level-set method were made by Bendsøe and Sigmund [2], Stolpe and Svanberg [3] and Michael et al. [4]. Up to now, topology optimization has received much success both in follow-up theoretical study and practical applications.
Now topology optimization is still developing rapidly to solve more complicated problems with the help of computing technology. Among those problems, the layout design of multi-component systems is to find not only the configuration of supporting structure but also the proper mounting positions of several components with predefined geometrical and physical properties. The idea can be expressed in Figure 1.
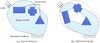 |
Figure 1. Illustration of integrated layout design of multi-component systems. |
Qian and Ananthasuresh [5], Xia et al. [6] and Zhang et al. [7] introduced different material interpolations including Heaviside function, level-set function and X-FEM to describe the components. Their methods hold the advantages of fixed mesh and analytical sensitivity analysis. However, the precise geometry properties cannot be ensured. Zhu et al. [8, 9, 10] developed the techniques of density point and embedded mesh to update the pseudo-density variables. At the same time, the finite circle method (FCM) is introduced to avoid the overlapping problem caused components and design domain boundaries. This method can keep the precise geometry properties of components but leads to element remeshing and difficulties in sensitivity analysis.
In our paper, we use the multi-point constraints to build the connection between components and structure, and its theory and advantages will be introduced below.
2 Formulation of layout design of multi-component systems
2.1 Formulation of MPC
Firstly, the design domain and components should be discretized into finite element, respectively, as shown in Figure 2. Assume P1 is one of the connecting nodes of the components, and is projected inside the design domain element e1. Then we enable the following MPC equation.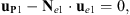 (1)where
(1)where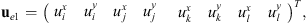 (2)where u
P1 denote the displacement vectors of node P1. ue1 and Ne1 are the displacement vectors of the element e1 and the shape function coefficient matrix at the position where P1 locates, respectively. The equation above indicates the displacements of node P1 is consistent with the point where it locates in the structure element.
(2)where u
P1 denote the displacement vectors of node P1. ue1 and Ne1 are the displacement vectors of the element e1 and the shape function coefficient matrix at the position where P1 locates, respectively. The equation above indicates the displacements of node P1 is consistent with the point where it locates in the structure element.
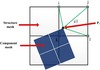 |
Figure 2. Illustration of MPC. |
When it involves several connecting nodes, the number of MPC equations will increase as a result. Actually, these MPC equations can be regarded as a linear combination of node displacements, so we can write it as the following form.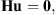 (3)where H is the coefficient matrix which is determined by shape functions of structure elements and coordinates of connecting nodes. u denotes the displacement vector of the structure system with components.
(3)where H is the coefficient matrix which is determined by shape functions of structure elements and coordinates of connecting nodes. u denotes the displacement vector of the structure system with components.
Considering the above displacement constraints, we use the Lagrange multiplier method to revise the overall potential energy of the global system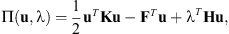 (4)where K is the global stiffness matrix. F is the nodal loads. λ is the Lagrange multiplier vector.
(4)where K is the global stiffness matrix. F is the nodal loads. λ is the Lagrange multiplier vector.
Then we have the Euler conditions for a stationary point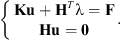 (5)
(5)
The displacement vector u and λ can be finally obtained by solving the above equations.
These constraint equations show much convenience since remeshing of structure elements around components is not needed and global stiffness matrix re-assembling process can be avoided when components move to different positions during optimization iterations. That brings high computing efficiency during optimization.
2.2 Optimization model
The goal of the optimization is to minimize the global strain energy of the structure system with a prescribed material volume fraction constraint. The design variables are the pseudo-density variables which control the material distribution and the geometry variables which describe the components’ status (locations and orientations). Extra geometrical non-overlapping constraints have to be imposed to avoid the components’ overlapping and keep all the components inside the design domain.
The optimization problem to minimize the strain energy of a multi-component system can be mathematically elaborated as: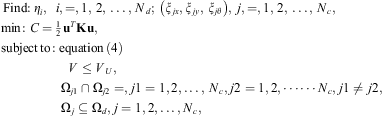 (6)where Nd and Nc are the numbers of the pseudo-density variables and the components, respectively. ξjx, ξjy and ξjθ are the geometry design variables i.e., the location and orientation related to the j th component. C is the strain energy of the structure system and K is the global stiffness matrix. V is the material volume fraction of the design domain with an upper limit of VU. Ωj, Ωj1 and Ωj are the areas of the jth, j1th and j2th components, respectively. Ωd denotes the area of the global design domain.
(6)where Nd and Nc are the numbers of the pseudo-density variables and the components, respectively. ξjx, ξjy and ξjθ are the geometry design variables i.e., the location and orientation related to the j th component. C is the strain energy of the structure system and K is the global stiffness matrix. V is the material volume fraction of the design domain with an upper limit of VU. Ωj, Ωj1 and Ωj are the areas of the jth, j1th and j2th components, respectively. Ωd denotes the area of the global design domain.
Different from previous mentioned material interpolation scheme SIMP or RAMP, here we use a polynomial material interpolation in the work of Zhu et al. [9].![$$ \mathrm{E}(i)=\left[\left(1-\alpha \right){\eta }_i^p+\alpha {\eta }_i)\right]{\mathrm{E}}_0(i), $$](/articles/smdo/full_html/2014/01/smdo130016/smdo130016-eq7.gif) (7)where ηi denotes the ith pseudo-density. E(i) stands for the corresponding Young’s modulus of one element, while E0(i) represents Young’s modulus of a solid element. p is the penalty factor and α is polynomial coefficient factor. In this study, p and α are set to be 4 and 1/16.
(7)where ηi denotes the ith pseudo-density. E(i) stands for the corresponding Young’s modulus of one element, while E0(i) represents Young’s modulus of a solid element. p is the penalty factor and α is polynomial coefficient factor. In this study, p and α are set to be 4 and 1/16.
Component layout design without non-overlapping constraints may lead to an unreasonable solution; even fails in optimization process especially when the number of components is very large. To deal with this problem, the finite circle method (FCM) is considered to be an effective mean. The main idea of FCM is illustrated in Figure 3: a series of circles are proposed to approximately describe the shape of two components and the rectangle design domain, so the overlap judgment of the two components or those of components and the structure design domain can be analytically evaluated by distance of the circles according to their center coordinates and radii.
 |
Figure 3. An example for the proposed FCM. |
3 Sensitivity analysis
3.1 Sensitivity analysis for pseudo density variables
Considering the static equation in equation (5), the differentiation with respect to the pseudo-density variable ηi can be written as: (8)
(8)
Assume F are design independent loads, so ∂F/∂ηi = 0, the equation below holds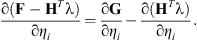 (9)
(9)
Then we have the derivative of the overall strain energy (10)
(10)
Substituting equations (8) and (9) into equation (10) and recalling ∂H
T
/∂ηi = 0, we yield: (11)
(11)
As u
T
H
T
= 0, equation (11) can be simplified as: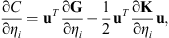 (12)where the derivatives of the stiffness matrix K can be easily obtained according to the material interpolation model for the element stiffness.
(12)where the derivatives of the stiffness matrix K can be easily obtained according to the material interpolation model for the element stiffness.
3.2 Sensitivity analysis for geometry design variables
According to the static equation of equation (4) and noting ∂F/∂ξj = 0, the differentiation with respect to one geometry variable ξj can be written as: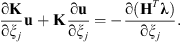 (13)
(13)
So the derivative of the strain energy with respect to the geometry design variable ξj is similarly written as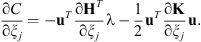 (14)
(14)
Suppose ξj is a translational variable of the jth component, both the stiffness matrix of the supporting structures and the components will remain unchanged after a translational moving. So we yield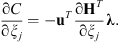 (15)
(15)
If ξj is a rotational variable, the stiffness matrix of the jth component after the rotation can be expressed as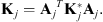 (16)
(16)
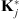 is the initial stiffness matrix of the jth component and Aj is the corresponding rotational transformation matrix. Suppose uj is the displacement vector of the jth component, then we can obtain
is the initial stiffness matrix of the jth component and Aj is the corresponding rotational transformation matrix. Suppose uj is the displacement vector of the jth component, then we can obtain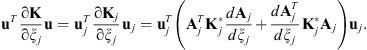 (17)
(17)
The derivative of the rotational transformation matrix can be easily calculated according to the coordinate transformation matrix.
Consequently, equation (14) can be written as: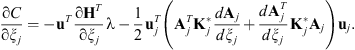 (18)
(18)
Now the final geometry sensitivities can be concluded as: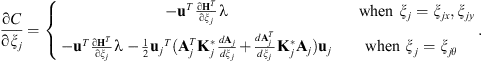 (19)
(19)
Note that H consists of the shape function coefficient matrix of the corresponding elements, which depend upon the connection positions and further the geometrical design variables describing the components’ locations and orientations.
4 Numerical test
As displayed in Figure 4, a rectangle structure with a size of 1.8 m × 0.6 m × 0.02 m acts as the design domain and is divided into one layer of 90 × 30 shell elements. The loads and boundary conditions applied to the structure are also shown in Figure 4, and remain unchanged in the optimization iterations. Two same complex components are bonded onto the design domain elements by using MPC through the connection nodes locate on in the centers of the holes also as in Figure 4. The material properties of the components are defined as: Ec = 2 × 1011 MPa and νc = 0.3. While the material property set for the supporting structure is Es = 7 × 1010 MPa and νs = 0.3.
 |
Figure 4. Optimization problem definition and illustration of the four-hole components. |
With a volume fraction upper limit constraint of 0.5 and non-overlapping constraints, final design is achieved after 55 iterations using GCMMA (Globally converged method of moving asymptotes) method. As shown in Figure 5a–5f, the components work positively as an inseparable part of the supporting structure to be subjected to loads. The iteration history of the objective function is shown in Figure 6. The stain energy value decreases from initial 0.00328J to final 0.000401J.
 |
Figure 5. Design history. |
 |
Figure 6. Iteration histories of the objective functions. |
Conclusion
In this paper, a simultaneous design method for structure system with multi-components is proposed. The connections are automatically generated with the help of MPC between supporting structure and components. Based on that connection type, fixed mesh, analytical sensitivities and precise geometry of components can be achieved at the same time. The test under static loads is numerically implemented. Through the optimal results above, the method developed for optimization problems of multi-component systems is evidently proved valid and reliable. Some engineering applications of large scale can be expected in the near future using that method.
Acknowledgments
This work is supported by National Natural Science Foundation for Distinguished Young Scholar (10925212), National Natural Science Foundation of China (90916027, 11002113, 51275424 and 11172236), 973 Program (2011CB610304), NPU Foundation for Fundamental Research (NPU-FFR-JC20120229), the 111 Project (B07050), NPU Foundation for Fundamental Research (NPU-FFR-JC20120229) and Graduate Starting Seed Fund of Northwestern Polytechnical University (Z2013050).
References
- Bendsøe MP, Kikuchi N. 1988. Generating optimal topologies in structural design using homogenization. Comput. Methods Appl. Mech. Engg., 71, 197–224. [Google Scholar]
- Bendsøe MP, Sigmund O. 2003. Topology Optimization: Theory, Method and Application. Springer/Heidelberg: Berlin/New York. [Google Scholar]
- Stolpe M, Svanberg K. 2001. An alternative interpolation scheme for minimum compliance topology optimization. Struct. Multidisc. Optim., 22, 116–124. [CrossRef] [MathSciNet] [Google Scholar]
- Michael YW, Wang XM, Guo DM. 2003. A level set method for structural topology optimization. Comput. Methods Appl. Mech. Engg., 192, 227–246. [Google Scholar]
- Qian ZY, Ananthasuresh GK. 2004. Optimal embedding of rigid objects in the topology design of structures. Mechanics Based Design of Structures and Machines, 32, 165–193. [Google Scholar]
- Xia L, Zhu JH, Zhang WH. 2012. Sensitivity analysis with the modified Heaviside function for the optimal layout design of multi-component systems. Comput. Methods Appl. Mech. Engg., 241–244, 142–154. [CrossRef] [Google Scholar]
- Zhang J, Zhang WH, Zhu JH. 2012. Integrated layout design of multi-component systems using XFEM and analytical sensitivity analysis. Comput. Methods Appl. Mech. Engg., 245–246, 75–89. [Google Scholar]
- Zhu JH, Zhang WH. 2010. Integrated layout design of supports and structures. Comput. Methods Appl. Mech. Engg., 199(9–12), 557–569. [CrossRef] [Google Scholar]
- Zhu JH, Zhang WH, Beckers P. 2009. Integrated layout design of multi-component system. Int. J. Numer. Meth. Engg., 78, 631–651. [CrossRef] [Google Scholar]
- Zhu JH, Zhang WH, Beckers P, Chen YZ, Guo ZZ. 2008. Simultaneous design of components layout and supporting structures using coupled shape and topology optimization. Struct. Multidisc. Optim., 36(1), 29–41. [CrossRef] [Google Scholar]
Cite this article as: Gao HH, Zhu JH & Zhang WH: A multi-point constraints based layout design of multi-component systems. Int. J. Simul. Multisci. Des. Optim., 2014, 5, A08.
All Figures
 |
Figure 1. Illustration of integrated layout design of multi-component systems. |
| In the text | |
 |
Figure 2. Illustration of MPC. |
| In the text | |
 |
Figure 3. An example for the proposed FCM. |
| In the text | |
 |
Figure 4. Optimization problem definition and illustration of the four-hole components. |
| In the text | |
 |
Figure 5. Design history. |
| In the text | |
 |
Figure 6. Iteration histories of the objective functions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




