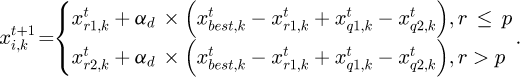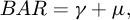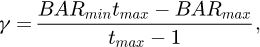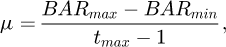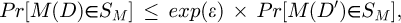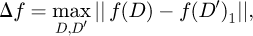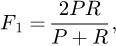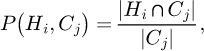| Issue |
Int. J. Simul. Multidisci. Des. Optim.
Volume 14, 2023
|
|
|---|---|---|
| Article Number | 13 | |
| Number of page(s) | 7 | |
| DOI | https://doi.org/10.1051/smdo/2023018 | |
| Published online | 27 November 2023 | |
Research article
Improved clustering algorithm for personal privacy and security protection of elderly consumers
Guangxi Electrical Polytechnic Institute, Nanning, Guangxi 530007, China
* e-mail: jiangju6838589@yeah.net
Received:
8
July
2023
Accepted:
24
October
2023
With the advancement of technology, there is an increasing emphasis on the personal privacy and security of elderly consumers. This article focuses on the personal privacy and security protection of elderly consumers. Based on the K-means (KM) clustering algorithm, the optimal value was obtained using the monarch butterfly optimization (MBO) algorithm. The migration operator and adjustment operator of the MBO algorithm were enhanced using differential variation algorithm and adaptive methods to obtain a modified monarch butterfly optimization (MMBO) algorithm. Then, to ensure secure protection during clustering, differential privacy (DP) was employed to add noise perturbation to data to obtained a method called DPMMBO-KM algorithm. In experiments on the UCI dataset, it was found that the MMBO-KM algorithm had better clustering performance. Taking the Iris dataset as an example, the MMBO-KM algorithm achieved the highest accuracy of 93.21%. In the application to recommendation systems, the DPMMBO-KM algorithm achieved higher F1 values under different privacy budgets; the average was 0.06. The results demonstrate that the improved clustering algorithm designed in this article can improve clustering results while ensuring personal privacy and data security, and also perform well in recommendation systems.
Key words: Clustering algorithm / elderly consumer / privacy security / differential privacy
© P. Jiang, Published by EDP Sciences, 2023
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Governments, enterprises, and other organizations rely on the collection and analysis of big data to provide reliable support for behavior prediction [1], customer segmentation [2], interest recommendation [3], and so on. However, while providing users with more accurate and reliable services through data mining, the leakage of users' personal information has also become an important issue [4]. For example, when developing personalized marketing plans for consumers, information such as users' addresses, phone numbers, and payment methods may be involved. Therefore, how to protect these personal privacy data has become a very important issue [5]. Currently, there are three main types of methods for protecting personal information. One type is data encryption, i.e., protecting data with encryption algorithms. Wang et al. [6] combined deep learning with homomorphic encryption to protect privacy information and found through experiments that the classification accuracy of encrypted data was close to plaintext, which proved the reliability of this method. Divya et al. [7] encrypted users' private information using the blowfish encryption algorithm, with key lengths ranging from 32 to 448 bits, and implemented this work in MATLAB. Another type is limited publication, i.e., releasing data through methods such as anonymization. Esmeel et al. [8] used K-anonymity technology to anonymize sensitive data in the dataset and verified through experiments that this method could balance data anonymity and utility. The last type is data distortion, i.e., modifying data to prevent attackers from reconstructing the data. Bugshan et al. [9] combined differential privacy (DP) and radial basis function (RBF) networks to enhance the privacy of data and verified through experiments the reasonable balance between accuracy and privacy of the method. DP is one type of data distortion method [10]. In this article, a modified clustering algorithm was proposed to protect the personal privacy and security of elderly consumers, combined with the DP algorithm, and applied to a recommendation system to demonstrate the effectiveness of this method. This study optimized the clustering algorithm to provide a new method for protecting personal privacy, which is beneficial for improving the effectiveness of recommendation systems while ensuring the protection of personal privacy and security.
2 Personal privacy security protection algorithm based on improved clustering
2.1 Clustering algorithm
Clustering is a method of partitioning a series of data into different groups in some way [11], where data within the same group have similar characteristics while differing significantly from data outside the group. K-means (KM) algorithm is a typical clustering algorithm [12]. It is assumed that dataset D is divided into k clusters, the data size is n, and the dimension is m. The clustering process is as follows.
k initial clustering centers are randomly selected.
The distance of sample x to k cluster centers is calculated.
Each sample is combined into the set with the smallest distance.
The center of each set is updated.
Steps (2)–(4) are looped until the algorithm converges, and the result is output.
However, the selection of the initial clustering center will affect the final clustering result. In addition, if the attacker obtains the clustering center and the distance from the sample to the clustering center, the real data of the sample will be easily deduced, resulting in the leakage of personal privacy data. Therefore, this paper improved the KM algorithm.
2.2 Improved monarch butterfly optimization algorithm
Swarm intelligence algorithms are often used to solve optimization problems, such as particle swarm algorithm (PSO) [13] and artificial bee colony (ABC) algorithm [14], which have good performance in fields such as Internet of Things [15]. The monarch butterfly optimization (MBO) algorithm is an algorithm that simulates the migration behavior of monarch butterflies [16]. It is assumed that there is a population of monarch butterflies called NP distributed in both Land1 and Land2, called subpopulation 1 and subpopulation 2, and the number of monarch butterflies in both subpopulations is the same. NP1 =ceil (p × NP), NP2 = N − NP1, where ceil(x) means rounding x . 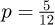 is the migration rate of monarch butterflies.
is the migration rate of monarch butterflies.
In the two subgroups, MBO updates the population by utilizing migration and adjustment operators in order to find the optimal value. However, MBO also suffers from the defects of single migration method and slow convergence; therefore, this paper improved its operator and designed a modified MBO (MMBO) on the basis of MBO.
First, for the migration operator, the differential variation algorithm is used for improvement.
where αd stands for the coefficient of variation, αd = rand, r is a random number, r = rand × peri, rand is a random number in [1], peri is a migration cycle, which is set as 1.2, 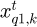 and
and 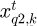 stand for random monarch butterfly locations,q1and q2 ∈ [1,N] , q1 ≠ q2 ≠ r1 ≠ r2.
stand for random monarch butterfly locations,q1and q2 ∈ [1,N] , q1 ≠ q2 ≠ r1 ≠ r2.
For the adjustment operator, the adaptive method is used for improvement:
where BAR stands for the adjustment rate, tmax stands for the maximum number of iterations, and BARmax and BARmin are the upper and lower bounds of BAR, [1].
The flow of the MMBO-based KM algorithm (MMBO-KM) is shown in Figure 1.
According to Figure 1, the MMBO algorithm was used to optimize the K-means algorithm.
Parameters and the monarch butterfly population are updated.
The position and fitness values of each monarch butterfly are calculated. After sorting from large to small, they are divided into NP1 and NP2.
NP1 is updated by the differential variation migration operator.
NP2 is updated by the adaptive adjustment algorithm.
A new population is obtained by merging NP1 and NP2.
t = t +1.
Whether or not the termination condition is met is determined. If not, it returns to step (2); if it is, the optimal k value of the KM algorithm is output.
Clustering is performed according to the KM algorithm.
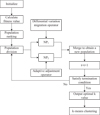 |
Fig. 1 The flow chart of the MMBO-KM algorithm. |
2.3 Differential privacy algorithm
DP is a method that uses data distortion to achieve the protection of personal private data security [17]. It is assumed that there is dataset D with a data size of n and a dimension of m. Various mapping functions of D are called query, F = {f1, f2, ⋯ , fn}.
Suppose there are two neighboring datasets, D and D′. If algorithm M satisfies the following equation, then it is said that M provides ε - differential privacy protection:
where SM ∈ Range (M) and ε denotes the privacy protection budget.
DP is implemented by noise perturbation mechanism, including Laplace mechanism and exponential mechanism. Laplace mechanism is the most common and the simplest. It is chosen in this paper to implement differential privacy protection:
where Δf is the global sensitivity and f is the query function.
Ultimately, the flow of the DPMMBO-KM algorithm is shown below.
The parameters are initialized. The optimal k value is obtained using the MMBO algorithm. The random disturbance noise is added to every initial center.
The distance between sample point xn and central point Ci (i = 1, 2, ⋯ k) is computed. Sample points are classified into the nearest set Sk.
The sum (sum) of attribute vector of sample points in different sets Si (i = 1, 2, ⋯ k) and the total number of sample points (num) are calculated. Laplace noise is added to obtain sum′ and num′.
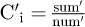 is updated to the new central point.
is updated to the new central point.Steps (2)–(4) are repeated constantly until the algorithm converges. The result is output.
2.4 Application of improved clustering algorithm for personal privacy and security protection of elderly consumers
The combination of DP and clustering algorithms has been widely applied in many scenarios, such as analyzing user behavior (e.g., customer classification for power companies or banks) or recommendation systems that handle users' private information. Therefore, research on DP clustering algorithms holds significant practical significance. The optimized clustering algorithm designed in this paper is applied to the recommendation system by taking the personal privacy and security protection of elderly consumers as an example. With the development and progress of society, more and more elderly people are shopping and consuming through the Internet, and shopping websites can achieve personalized recommendations for elderly consumers by processing and analyzing their consumption behavior data, so as to obtain higher revenues. In this process, the improved clustering algorithm designed in this paper is applied to personalized recommendations for elderly consumers in order to protect their personal privacy and security.
The collaborative filtering (CF) algorithm [18] is used as the basis, and it is combined with the improved clustering algorithm to protect the data in K-means by differential privacy. The specific process is described below.
User-item scoring matrix R(U1, I) is established. U1 stands for a dataset, and I is the set of item scores.
The matrix is clustered by the improved clustering algorithm.
The similarity between target user u in test set U2 and various cluster centers is calculated to find N nearest neighbors of u.
The items that are not scored by u are predicted according to the scores of the nearest neighbor users.
n items with the highest predictive score are recommended to u.
3 Experimental results and analysis
3.1 Experiment settings
The experiments were performed in the Windows 10 environment, and the programming language was Python. For the MMBO algorithm, the maximum number of iterations was set to 100, and the population size was 100. The ten-fold cross-validation was used, and the results were averaged. The dataset used consists of two parts.
UCI dataset [19]: it is commonly used for testing machine learning, including data in medical, biological and other aspects. In this paper, the clustering performance of the optimized clustering algorithm was evaluated using the UCI dataset (Tab. 1).
Elderly consumers' consumption behavior dataset: using a crawler to crawl the data of elderly consumers (age ≥ 60 yr old) on Taobao.com, 101,256 rating data of 956 elderly consumers for 1,894 products were collected. The five-point scale was used; the higher the score, the higher the satisfaction level of the consumer. Some of the data are displayed in Table 2.
Experimental dataset.
Consumer behavior data set of the elderly consumers.
3.2 Evaluation indicators
– F1 value: it is used to evaluate the clustering effect. It is assumed that the classification result of manual labeling is Hi, the classification result obtained by the algorithm is Cj, then the F1 value is:
where P denotes the accuracy and R denotes the recall rate.
– Mean absolute error (MAE): it is used to assess the effectiveness of the recommendation system in rating prediction:
where Pu,r is the score predicted by the algorithm, and Ru,r is user u's real rating of item r.
3.3 Analysis of results
First, the following methods were compared using the UCI dataset:
The traditional KM algorithm,
The PSO-KM algorithm that uses the PSO algorithm to obtain the optimal k value,
The MBO-KM algorithm that uses the MBP algorithm to obtain the optimal k value,
The MMBO-KM algorithm that uses the MMBO algorithm to obtain the optimal k value.
The clustering results of the above four methods for the UCI dataset were compared, as shown in Figure 2.
From Figure 2, it was found that the accuracy of the MMBO-KM algorithm was significantly higher than that of the other methods. Taking Iris as an example, the accuracy of the traditional KM algorithm was 80.21%, and the accuracy of the PSO-KM algorithm was 85.67%, which was 5.46% higher than that of the traditional K-means algorithm; the accuracy of the MBO-KM algorithm was 91.26%, which was 5.59% higher than that of the PSO-KM algorithm, verifying the performance of the MBO algorithm in parameter optimization. The accuracy of the MMBO-KM algorithm reached 93.21% for Iris, which was 1.95% higher than that of the MBO-KM algorithm. The results proved the effectiveness of the improvement of the MBO algorithm and the improvement of the clustering effect of the KM algorithm.
Then, the effectiveness of the DPMMBO-KM algorithm on privacy protection was analyzed, and it was also compared with the DP-KM algorithm without parameter optimization. Privacy budget ϵ was set to different values. Taking Iris as an example, the changes in the F1 value of the two algorithms are shown in Figure 3. The method proposed in this article optimized the initial cluster centers using the MMBO algorithm, thereby eliminating the randomness of the KM algorithm in selecting initial cluster centers and enhancing clustering effectiveness.
As shown in Figure 3, when ε = 0.2, the F1 values of both DP-KM and DPMMBO-KM algorithms were not high, but the F1 value of the DPMMBO-KM algorithm was 15.44% higher than the DP-KM algorithm, which indicated that after the optimal k value selection, the algorithm still maintained a good clustering effect after adding the privacy budget. With the ε value kept increasing, the F1 values of both algorithms showed an increase, but the F1 value of the DP-KM algorithm was always lower than that of the DPMMBO-KM algorithm. As the DP-KM algorithm did not go through the optimal value k value selection, the randomly selected initial centers was greatly influenced by random noise, which had a negative impact on the clustering effect. As shown in Figure 2, when ε = 1, the F1 value of the DPMMBO-KM algorithm was 20.1% higher than the DP-KM algorithm, which proved that the method had a good clustering effect while improving data security. The DPMMBO-KM algorithm consistently maintained a higher F1 score than the DP-KM algorithm under different privacy budgets, further demonstrating the importance of selecting the optimal value and validating the effectiveness of MMBO optimization.
Finally, the rating prediction performance of the DPMMBO-KM algorithm was analyzed on the recommendation system and compared with the traditional KM-based recommendation algorithm. The number of nearest neighbors, N, was set to 10–50. The comparison of the MAE is presented in Figure 4.
From Figure 4, firstly, it was found that the larger the number of nearest neighbors (N), the smaller the gap between the algorithm's predicted results and the true ratings, and the more the recommended results match the orientation of elderly consumers, i.e., the better the recommendations. In comparison, the recommendation algorithm based on traditional KM algorithm had no noise interference, and its MAE value was always lower than that of the DPMMBO-KM algorithm. However, the gap between the two algorithms became smaller and smaller, and when N = 50, the difference of MAE was only 0.1082. Compared to the traditional KM algorithm, the DPMMBO-KM algorithm sacrificed a certain degree of accuracy in score prediction; however, the resulting error was minimal and did not significantly impact recommendation results. Additionally, it achieved the protection of personal privacy data for elderly individuals. In conclusion, the DPMMBO-KM algorithm can obtain good recommendation results while ensuring that original data is not leaked, making it more applicable in practical scenarios.
Taking 20 samples as examples, the comparison of predicted scores with the real scores of elderly consumers is demonstrated in Figure 5.
As shown in Figure 5, the ratings predicted by the DPMMBO-KM-based recommendation algorithm agreed well with the actual ratings of elderly consumers, with small differences. Among the 20 samples, the maximum prediction error was 0.18, the minimum was 0.01, and the average was 0.06. This result indicated that applying the optimized clustering algorithm designed in this paper to the recommendation system could not only protect the personal privacy and security of elderly consumers, but also ensure the effectiveness of the recommendation results.
 |
Fig. 2 Comparison of clustering effects between different methods. |
 |
Fig. 3 Comparison of F1 values under different privacy budgets. |
 |
Fig. 4 Comparison of the score prediction performance between algorithms. |
 |
Fig. 5 Comparison of predicted and real scores of elderly consumers. |
4 Conclusion
This paper improved the KM algorithm by optimizing the initial clustering centers and adding privacy protection to obtain the DPMMOB-KM algorithm, which was applied to the recommendation system for elderly consumers. Through experiments, it was found that the clustering performance of the MMBO-KM algorithm, which obtained the optimal k value using the MMBO algorithm, was significantly improved, with a clustering accuracy of 93.21% for the Iris dataset. After adding differential privacy protection, the DPMMOB-KM algorithm still had a high F1 value and better clustering performance than the DP-KM algorithm. Finally, when comparing the recommendation effects for elderly consumers, the recommendation system based on the improved clustering algorithm had a small MAE value, and the difference between the rating predicted by the algorithm and the actual rating of the elderly consumers was very small, indicating that the system can ensure accurate recommendation while protecting the privacy of elderly consumers. While this study has yielded some results, there are still limitations. For instance, although the addition of MMBO optimization has improved the clustering performance of the algorithm, it has also increased its complexity. It remains unclear whether there exist better optimization algorithms than the MMBO algorithm. In future research, a more comprehensive analysis of the proposed algorithm's performance is needed to explore ways to enhance clustering effectiveness while reducing algorithmic complexity. Additionally, investigating the possibility of integrating DP with alternative clustering algorithms apart from the KM algorithm should also be considered.
References
- S.D. Anogiannakis, P.C. Petris, D.N. Theodorou, Promising route for the development of a computational framework for self-assembly and phase behavior prediction of ionic surfactants using martini, J. Phys. Chem. B, 124, 556–567 (2020) [CrossRef] [Google Scholar]
- S.P. Othayoth, R. Muthalagu, Customer segmentation using various machine learning techniques, Int. J. Busin. Intell. Data Min. 2022, 20 (2022) [Google Scholar]
- I. Wijaya, Mudjahidin, Development of conceptual model to increase customer interest using recommendation system in e-commerce, Proc. Comput. Sci. 197, 727–733 (2022) [CrossRef] [Google Scholar]
- L. Baker-Eveleth, R. Stone, D. Eveleth, Understanding social media users' privacy-protection behaviors, Inf. Comput. Secur. 30, 324–345 (2022) [CrossRef] [Google Scholar]
- S. Salim, B. Turnbull, N. Moustafa, Data analytics of social media 3.0: privacy protection perspectives for integrating social media and internet of things (SM-IoT) systems, Ad. Hoc. Netw. 128, 1–15 (2022) [Google Scholar]
- Y. Wang, X. Liang, X. Hei, W. Ji, L. Zhu, Deep learning data privacy protection based on homomorphic encryption in AIoT, Mob. Inf. Syst. 2021, 1–11 (2021) [Google Scholar]
- S. Divya, K.V. Prema, B. Muniyal, Privacy preservation mechanism for the data used in image authentication, 2019 IEEE International Conference on Distributed Computing, VLSI, Electrical Circuits and Robotics (DISCOVER), Manipal, India, 2019, pp. 1–6 [Google Scholar]
- T.K. Esmeel, M.M. Hasan, M.N. Kabir, A. Firdaus, Balancing data utility versus information loss in data-privacy protection using k-anonymity, 2020 IEEE 8th Conference on Systems, Process and Control (ICSPC), Melaka, Malaysia, 2020, pp. 158–161 [Google Scholar]
- N. Bugshan, I. Khalil, N. Moustafa, M. Almashor, A. Abuadbba, Radial basis function network with differential privacy, Future Gener. Comp. Sy. 127, 473–486 (2022) [CrossRef] [Google Scholar]
- T. Murakami, H. Hino, J. Sakuma, Toward distribution estimation under local differential privacy with small samples, Proc. Priv. Enhancing Technol. 2018, 84–104 (2018) [CrossRef] [Google Scholar]
- R.K. Bono, J.A. Tarduno, M.S. Dare, G. Mitra, R.D. Cottrell, Cluster analysis on a sphere: application to magnetizations from metasediments of the Jack Hills, Western Australia, Earth Planet. Sc. Lett. 484, 67–80 (2018) [CrossRef] [Google Scholar]
- A. Bigdeli, A. Maghsoudi, R. Ghezelbash, Application of self-organizing map (SOM) and K-means clustering algorithms for portraying geochemical anomaly patterns in Moalleman district, NE Iran, J. Geochem. Explor. 233, 1–13 (2022) [Google Scholar]
- K. Envelope, S.D. Singh, S. Adhikari, Implementation of genetic and particle swarm optimization algorithm for voltage profile improvement and loss reduction using capacitors in 132 kV Manipur transmission system, Energy Rep. 9, 738–746 (2023) [CrossRef] [Google Scholar]
- M. Souier, Z. Sari, A.O. Khedim, Combinatorial artificial bee colony algorithm hybridized with a new release of iterated local search for job-shop scheduling problem, Int. J. Oper. Res. 44, 435–461 (2022) [CrossRef] [MathSciNet] [Google Scholar]
- S. Sennan, S. Ramasubbareddy, S. Balasubramaniyam, A. Nayyar, M. Abouhawwash, N. Hikal, T2FL-PSO: type-2 fuzzy logic-based particle swarm optimization algorithm used to maximize the lifetime of internet of things, IEEE Access 9, 63966–63979 (2021) [CrossRef] [Google Scholar]
- M. Ghetas, C.H. Yong, P. Sumari, Harmony-based monarch butterfly optimization algorithm, 2015 IEEE International Conference on Control System, Computing and Engineering (ICCSCE), Penang, Malaysia, 2015, pp. 156–161 [Google Scholar]
- J. Laeuchli, Y. Ramírez-Cruz, R. Trujillo-Rasua, Analysis of centrali+ty measures under differential privacy models, Appl. Math. Comput. 412, 126546 (2022) [Google Scholar]
- S. Poudel, M. Bikdash, Optimal dependence of performance and efficiency of collaborative filtering on random stratified subsampling, Big Data Min. Anal. 5, 192–205 (2022) [CrossRef] [Google Scholar]
- A.B. Buriro, B. Ahmed, G. Baloch, J. Ahmed, R. Shoorangiz, S.J. Weddell, R.D. Jones, Classification of alcoholic EEG signals using wavelet scattering transform-based features, Comput. Biol. Med. 139, 104969 (2021) [CrossRef] [Google Scholar]
Cite this article as: Pengfei Jiang, Improved clustering algorithm for personal privacy and security protection of elderly consumers, Int. J. Simul. Multidisci. Des. Optim. 14, 13 (2023)
All Tables
All Figures
 |
Fig. 1 The flow chart of the MMBO-KM algorithm. |
| In the text | |
 |
Fig. 2 Comparison of clustering effects between different methods. |
| In the text | |
 |
Fig. 3 Comparison of F1 values under different privacy budgets. |
| In the text | |
 |
Fig. 4 Comparison of the score prediction performance between algorithms. |
| In the text | |
 |
Fig. 5 Comparison of predicted and real scores of elderly consumers. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.